
L’étude des suites de Cauchy et des espaces complets figurait autrefois aux programmes de mathématiques du 1er cycle universitaire et des classes préparatoires scientifiques. Ce n’est plus le cas aujourd’hui, ce que certains (j’en suis) peuvent déplorer. Voir à ce sujet cet échange (qui remonte à 2015) sur le site du Images des mathématiques du CNRS.
Le présent article est écrit à l’intention de celles et ceux qui souhaiteraient s’initier à ce sujet passionnant, afin d’élargir leur point de vue sur les questions d’analyse réelle.
1 – La définition de la convergence ne suffit pas
Commençons par le commencement : que signifie qu’une suite réelle est convergente ?
Définition
Une suite réelle ![]() est dite convergente lorsqu’il existe un nombre réel
est dite convergente lorsqu’il existe un nombre réel ![]() tel que l’écart entre
tel que l’écart entre ![]() (le
(le ![]() ème terme de la suite
ème terme de la suite ![]() et
et ![]() devient arbitrairement petit, à partir d’un certain rang.
devient arbitrairement petit, à partir d’un certain rang.
En symboles :
![Rendered by QuickLaTeX.com \[\boxed{\begin{array}{c}\exists L\in\mathbb{R};\thinspace\forall\epsilon>0,\exists N\in\mathbb{N};\thinspace\forall n\in\mathbb{N},\\n\geqslant N\Rightarrow\left|u_{n}-L\right|\leqslant\epsilon\\\end{array}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b9e13d7a27be356d7549f5de732f771e_l3.png)
On peut prouver l’unicité d’un tel nombre ![]() (voir l’encadré ci-dessous). En cas d’existence, on dit que
(voir l’encadré ci-dessous). En cas d’existence, on dit que ![]() est la limite de la suite
est la limite de la suite ![]() qu’on note au choix
qu’on note au choix ![]() ou bien
ou bien ![]()
Unicité de la limite (cliquer pour déplier / replier)
Supposons que la suite ![]() converge vers
converge vers ![]() et vers
et vers ![]()
Etant donné ![]() il existe un couple
il existe un couple ![]() d’entiers naturels tel que :
d’entiers naturels tel que :
![Rendered by QuickLaTeX.com \[\begin{array}{cc}\forall k\geqslant N, & \left|u_{k}-L\right|\leqslant\frac{\epsilon}{2}\\\\\forall k\geqslant N', & \left|u_{k}-L'\right|\leqslant\frac{\epsilon}{2}\end{array}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ac8269e1d14218374629c660d03c5be7_l3.png)
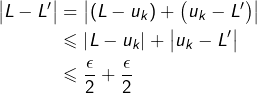
![]()
Un constat s’impose :
Si l’on veut établir la convergence d’une suite réelle, en appliquant strictement la définition, alors il faut connaître à l’avance la valeur de la limite.
Dans certains cas simples, ce n’est pas gênant …
Exemple 1
Supposons qu’on veuille établir la convergence de la suite de terme général :
![]()
On commence par ré-écrire cette expression sous une forme plus maniable.
Pour tout ![]() :
:
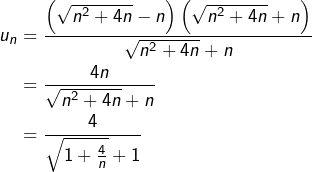
Il reste à établir cela rigoureusement, en utilisant la définition de la convergence.
On se donne un réel ![]() et l’on tâche de montrer que :
et l’on tâche de montrer que :
![]()
On peut observer que :
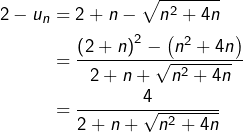
![]()
![]()
![]()
On constate que :
![]()
Mais en général, les choses ne sont pas aussi simples …
Exemple 2
Considérons maintenant la suite de terme général :
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=0}^{n}\frac{\cos\left(k^{2}\right)}{2^{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-66fce1e68980e95ca94878441ea9cde4_l3.png)
Et à supposer qu’elle converge, la valeur de sa limite n’est pas claire non plus …
L’idéal serait un outil permettant d’affirmer la convergence d’une suite, mais sans qu’il soit nécessaire de deviner à l’avance la limite.
Bonne nouvelle : cet outil existe !
Il a été indépendamment découvert / inventé par B. Bolzano et A-L. Cauchy, dans la première moitié du XIXème siècle.


2 – Le critère de Cauchy
Définition
Une suite réelle ![]() est de Cauchy lorsque l’écart entre deux termes devient arbitrairement petit à partir d’un certain rang.
est de Cauchy lorsque l’écart entre deux termes devient arbitrairement petit à partir d’un certain rang.
En symboles :
![Rendered by QuickLaTeX.com \[\boxed{\begin{array}{c}\forall\epsilon>0,\exists N\in\mathbb{N},\forall\left(p,q\right)\in\mathbb{N}^{2},\\\left(p\geqslant N\text{ et }q\geqslant N\right)\Rightarrow\left|u_{p}-u_{q}\right|\leqslant\epsilon\end{array}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bebcf41bf3a8ede8ceab4dd2f59afed6_l3.png)
On peut reformuler cette condition sous la forme :
![]()
Il est facile de voir que :
Proposition
Toute suite réelle convergente est de Cauchy.
Preuve (cliquer pour déplier / replier)
Soit ![]() une suite réelle convergente, de limite
une suite réelle convergente, de limite ![]() Etant donné
Etant donné ![]() il existe
il existe ![]() tel que :
tel que :
![]()
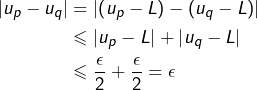
Mais le plus intéressant réside dans la réciproque, que nous admettrons dans cet article :
Théorème (critère de Cauchy)
Toute suite réelle de Cauchy est convergente.
Dans son cours d’analyse de 1821, Cauchy considérait que le critère qui porte aujourd’hui son nom était clairement équivalent à la convergence. Pourtant, il n’y avait là rien d’évident … mais surtout : le concept précis de nombre réel n’avait pas encore été défini ! Il fallait pour cela attendre encore quelques décennies.
C’est principalement à Georg Cantor , mais aussi à Eduard Heine et Charles Meray que revient le mérite d’avoir élaboré, à la fin du XIXème siècle, une construction rigoureuse du corps des réels et d’avoir, par là-même, fourni une démonstration de l’équivalence entre la définition de la convergence et le critère de Cauchy.
Les détails d’une telle construction sont brièvement évoqués dans le lexique mathématique.
Reprenons la suite ![]() définie à la fin de la section précédente :
définie à la fin de la section précédente :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\thinspace S_{n}=\sum_{k=0}^{n}\frac{\cos\left(k^{2}\right)}{2^{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eebaf4d2a126f74fe09d3952b8869178_l3.png)
Pour tout couple ![]() tel que
tel que ![]() :
:
![Rendered by QuickLaTeX.com \[S_{q}-S_{p}=\sum_{k=p+1}^{q}\frac{\cos\left(k^{2}\right)}{2^{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-79ca42ac8bcbb0cb9cd938cd20c519e9_l3.png)
![Rendered by QuickLaTeX.com \[\left|S_{q}-S_{p}\right|\leqslant\sum_{k=p+1}^{q}\frac{\left|\cos\left(k^{2}\right)\right|}{2^{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f381884bdf45e074d43cdcec758eb906_l3.png)
![Rendered by QuickLaTeX.com \[\left|S_{q}-S_{p}\right|\leqslant\sum_{k=p+1}^{q}\frac{1}{2^{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d6defe02ef88c35c69729746aeb0f8af_l3.png)
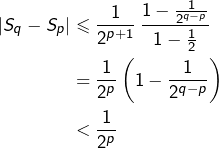
Bref, la suite ![]() est de Cauchy et donc, elle converge (mais on ne sait pas trop vers quoi).
est de Cauchy et donc, elle converge (mais on ne sait pas trop vers quoi).
Cet exemple se généralise largement : voir la section 7.

Avant de quitter cette section, signalons une confusion fréquente.
Pour une suite réelle ![]() le fait que
le fait que ![]() soit de Cauchy n’est pas équivalent à
soit de Cauchy n’est pas équivalent à
(![]() )
) ![]()
Par exemple, la suite de terme général :
![Rendered by QuickLaTeX.com \[H_{n}=\sum_{k=1}^{n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1e9e62ff52597157f7ef82d4b070212a_l3.png)
- d’une part, en notant
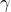 la constante d’Euler, pour tout
la constante d’Euler, pour tout 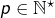 fixé, on a lorsque
fixé, on a lorsque 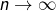 :
:
donc :![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}0<H_{n+p}-H_{n} & = \ln\left(n+p\right)+\gamma+o\left(1\right)-\left[\ln\left(n\right)+\gamma+o\left(1\right)\right]\\ & = \ln\left(1+\frac{p}{n}\right)+o\left(1\right) \end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-1de15467514ab4c3caa3a6eff09dd3ce_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\left(H_{n+p}-H_{n}\right)=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1de0f3625b18d1cef0a8b36862f7e9c5_l3.png)
- et d’autre part, pour tout
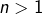 :
:![Rendered by QuickLaTeX.com \[H_{2n}-H_{n}=\sum_{k=n+1}^{2n}\frac{1}{k}>\frac{1}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a81dfaefe97d22f18f23d9f92114acb6_l3.png)
3 – Limite monotone
L’énoncé suivant, qui est admis en fin de lycée, est très utile. C’est le théorème de la limite monotone, en abrégé TLM :
TLM
Toute suite réelle, croissante et majorée, est convergente.
Bien entendu, toute suite réelle décroissante et minorée est aussi convergente (on le voit aussitôt en appliquant le TLM à la suite opposée).
Comme expliqué plus haut, le critère de Cauchy permet de prouver la convergence (éventuelle) d’une suite réelle, sans avoir à connaître sa limite à l’avance. Le TLM présente visiblement le même avantage. On pourrait donc penser que, tous comptes faits, le critère de Cauchy est un gadget superflu. C’est inexact, pour deux raisons :
- Contrairement au critère de Cauchy qui donne une condition nécessaire et suffisante de convergence (c’est d’ailleurs le sens du mot critère) — le TLM ne donne qu’une condition suffisante (et non nécessaire) de convergence. Par exemple, la suite de terme général
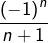 converge vers 0, mais n’est monotone à partir d’aucun rang.
converge vers 0, mais n’est monotone à partir d’aucun rang. - Le TLM repose sur le théorème de la borne supérieure, qui repose sur le critère de Cauchy.
Théorème (de la borne supérieure)
Toute partie non vide et majorée de ![]() possède une borne supérieure (c’est-à-dire un plus petit majorant).
possède une borne supérieure (c’est-à-dire un plus petit majorant).
La preuve de ce résultat est reportée en annexe. Pour le moment, démontrons le TLM.
Preuve du TLM (cliquer pour déplier / replier)
Soit ![]() une suite réelle croissante et majorée. L’ensemble
une suite réelle croissante et majorée. L’ensemble ![]() est une partie de
est une partie de ![]() non vide et majorée, donc possède une borne supérieure
non vide et majorée, donc possède une borne supérieure ![]()
Etant donné ![]() le réel
le réel ![]() est le plus petit majorant de
est le plus petit majorant de ![]() donc
donc ![]() n’est pas un majorant de cet ensemble. Ceci signifie qu’il existe un élément de
n’est pas un majorant de cet ensemble. Ceci signifie qu’il existe un élément de ![]() strictement supérieur à
strictement supérieur à ![]()
Autrement dit :
![]()
Mais d’une part, ![]() est croissante donc
est croissante donc ![]() pour tout
pour tout ![]()
Et d’autre part, ![]() (et a fortiori
(et a fortiori ![]() ) pour tout
) pour tout ![]() puisque
puisque ![]() est un majorant de
est un majorant de ![]() Ainsi :
Ainsi :
![]()
On a prouvé que toute suite réelle croissante et majorée, converge vers la borne supérieure de l’ensemble de ses termes.
4 – Le théorème du point fixe de Picard
Vous avez peut-être déjà observé, en jouant avec une calculette, qu’en partant d’un quelconque nombre strictement positif et en appuyant plusieurs fois de suite sur la touche racine carrée, la valeur affichée semble converger vers 1.
L’illustration dynamique ci-dessous permet de visualiser ce phénomène.
Illustration dynamique
Le graphe rouge est celui de la fonction racine carrée. La droite bleue est la première bissectrice, d’équation ![]()
Le slider permet de choisir un nombre positif ![]() En pressant plusieurs fois sur le bouton SQRT on déclenche le calcul des premiers termes de la suite définie par :
En pressant plusieurs fois sur le bouton SQRT on déclenche le calcul des premiers termes de la suite définie par :
![]()
La dernière valeur calculée est affichée sous le slider. C’est l’abscisse du petit spot vert, visible à l’extrémité de la ligne polygonale blanche.
Les boutons ZIN et ZOUT permettent d’effectuer un zoom avant / arrière.
Une pression sur RESET remet tous les paramètres à leurs valeurs d’origine.
On verra, en fin de section, comment traiter cet exemple de manière directe ou bien comme cas particulier du théorème de Picard ci-dessous.
Considérons un intervalle ![]() non trivial (c’est-à-dire de longueur non nulle), une application
non trivial (c’est-à-dire de longueur non nulle), une application ![]() et un réel
et un réel ![]()
On peut définir une suite en itérant ![]() à partir de
à partir de ![]() Cela consiste à poser :
Cela consiste à poser :
(✯) ![Rendered by QuickLaTeX.com \[\boxed{\left\{ \begin{array}{c}u_{0}=s\\\\\forall n\in\mathbb{N},u_{n+1}=f\left(u_{n}\right)\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-19876a747ffd66b73b47f6b3ec7e34f7_l3.png)
➡ Une telle suite n’a aucune raison de converger, même si ![]() est continue. Par exemple, si l’on choisit :
est continue. Par exemple, si l’on choisit :
![Rendered by QuickLaTeX.com f:\left[0,1\right]\rightarrow\left[0,1\right],\thinspace t\mapsto1-t](https://math-os.com/wp-content/ql-cache/quicklatex.com-5b3916c072c00ddd976578d68a995930_l3.png)
![Rendered by QuickLaTeX.com s\in\left[0,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-698192d5d838fd5dc67160175037616c_l3.png) tel que
tel que 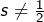
alors, pour tout ![]() :
:
![]()
➡ Si la suite ![]() converge, sa limite dépend en général du choix de
converge, sa limite dépend en général du choix de ![]() Considérons par exemple :
Considérons par exemple :
Dans ce cas (peu passionnant, j’en conviens), la suite ![]() est constante (donc convergente !) et sa limite est
est constante (donc convergente !) et sa limite est ![]()
➡ La nature (convergence ou divergence) de la suite ![]() peut dépendre de
peut dépendre de ![]() C’est par exemple le cas lorsque :
C’est par exemple le cas lorsque :
![]()
Toutefois, et moyennant des hypothèses convenables, on peut garantir que :
- la suite
 converge, quelle que soit la valeur de
converge, quelle que soit la valeur de 
- sa limite est indépendante de
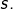
Théorème (Picard)
Soit ![]() un intervalle fermé non trivial.
un intervalle fermé non trivial.
Si ![]() est contractante, alors :
est contractante, alors :
 possède un unique point fixe
possède un unique point fixe 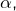
- pour tout
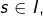 la suite
la suite  définie par (✯) converge vers
définie par (✯) converge vers 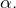
Expliquons d’abord le vocabulaire :
➡ l’hypothèse ![]() fermé signifie que, pour toute suite convergente à termes dans
fermé signifie que, pour toute suite convergente à termes dans ![]() la limite de cette suite appartient à
la limite de cette suite appartient à ![]()
➡ l’hypothèse ![]() contractante signifie qu’il existe
contractante signifie qu’il existe ![]()
tel que :
(![]() )
) ![]()
➡ un point fixe de ![]() est un réel
est un réel ![]() vérifiant
vérifiant ![]()
La preuve ci-dessous repose sur la complétude de ![]() c’est-à-dire sur le fait que toute suite réelle de Cauchy est convergente.
c’est-à-dire sur le fait que toute suite réelle de Cauchy est convergente.
Preuve du théorème de Picard (cliquer pour déplier / replier)
Si ![]() et
et ![]() sont des points fixes de
sont des points fixes de ![]() alors :
alors :
![]()
Montrons simultanément l’existence d’un point fixe pour ![]() et le fait que toute suite définie par itération de
et le fait que toute suite définie par itération de ![]() converge vers cette valeur.
converge vers cette valeur.
Soit ![]() et soit
et soit ![]() la suite définie par les relations :
la suite définie par les relations :
![]()
![]()
C’est visiblement le cas pour ![]() 0.
0.
Et si cette inégalité est vraie pour un certain ![]() alors :
alors :
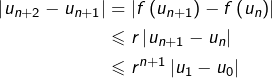
Maintenant, considérons deux entiers naturels ![]() tels que
tels que ![]() Alors :
Alors :
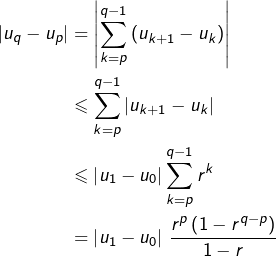
![]()
Comme la suite géométrique ![]() converge vers 0, alors étant donné
converge vers 0, alors étant donné ![]() il existe certainement un entier naturel
il existe certainement un entier naturel ![]() tel que :
tel que :
![]()
La suite ![]() est donc de Cauchy.
est donc de Cauchy.
Elle converge vers un certain réel ![]() qui appartient à
qui appartient à ![]() puisque
puisque ![]() est fermé.
est fermé.
Le caractère contractant de ![]() entraînant sa continuité, on peut passer à la limite dans l’égalité
entraînant sa continuité, on peut passer à la limite dans l’égalité ![]() ce qui donne
ce qui donne ![]()
Revenons maintenant à l’exemple de la racine carrée, évoqué au début de cette section.
Pour cet exemple simple, l’usage du théorème de Picard ne s’impose pas. En effet :
- chacun des intervalles
![Rendered by QuickLaTeX.com \left[0,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-beb10f64e7f6b1b271629e3a8291d2e5_l3.png) et
et 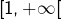 est stable par
est stable par 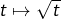
- pour tout
![Rendered by QuickLaTeX.com t\in\left[0,1\right],\thinspace\sqrt{t}\geqslant t](https://math-os.com/wp-content/ql-cache/quicklatex.com-24c00a81f4f24bcdfb8bdb068d9608c5_l3.png)
- pour tout
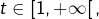
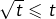
Il en résulte que la suite définie par
![]()
- croissante et majorée par 1, si
![Rendered by QuickLaTeX.com s\in\left]0,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-76f36af3d615301fee546aa19a7095b7_l3.png)
- décroissante et minorée par
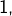 si
si 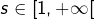
Elle converge donc dans tous les cas, et sa limite ![]() vérifie la condition
vérifie la condition ![]() (obtenue en passant à la limite dans la formule de récurrence).
(obtenue en passant à la limite dans la formule de récurrence).
Comme ![]() (une suite croissante dont le premier terme est strictement positif ne peut pas converger vers 0, une suite minorée par 1 non plus), alors
(une suite croissante dont le premier terme est strictement positif ne peut pas converger vers 0, une suite minorée par 1 non plus), alors ![]()
Cela dit, on peut tout de même faire intervenir le théorème de Picard, ce qui apporte un éclairage un peu différent sur la même question.
Pour tout couple ![]() de réels tels que
de réels tels que ![]() :
:
![]()
Ainsi, pour ![]() la suite converge vers 1 (l’unique point fixe de
la suite converge vers 1 (l’unique point fixe de ![]()
Et si ![]() alors il existe un entier
alors il existe un entier ![]() tel que
tel que ![]() car, dans le cas contraire, on aurait :
car, dans le cas contraire, on aurait :
![]()
![]()
5 – Espaces métriques complets
Les notions de suite convergente et de suite de Cauchy ont été définies dans le contexte des nombres réels.
Ce cadre peut être considérablement élargi, en remplaçant ![]() et la valeur absolue par un ensemble abstrait
et la valeur absolue par un ensemble abstrait ![]() et une distance
et une distance ![]() sur
sur ![]() .
.
Définition 3
Un espace métrique est un ensemble ![]() sur lequel on a défini une distance, c’est-à-dire une application
sur lequel on a défini une distance, c’est-à-dire une application ![]() vérifiant les conditions suivantes :
vérifiant les conditions suivantes :
![]()
![]()
![]()
![]()
(1)
(2)
(3)
La condition (1) exprime la symétrie de l’application ![]() .
.
La condition (2) est appelée inégalité triangulaire.
La condition (3) est appelée « condition de séparation ».
➡ Une suite ![]() à termes dans
à termes dans ![]() est dite convergente lorsqu’il existe un élément
est dite convergente lorsqu’il existe un élément ![]() de
de ![]() tel que :
tel que :
![Rendered by QuickLaTeX.com \[\boxed{\begin{array}{c}\forall\epsilon>0,\thinspace\exists N\in\mathbb{N};\thinspace\forall n\in\mathbb{N},\\n\geqslant N\Rightarrow d\left(u_{n},L\right)\leqslant\epsilon\end{array}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d6112a5dfec12964a2e29138149f7f3c_l3.png)
➡ Elle est dite de Cauchy lorsque :
![Rendered by QuickLaTeX.com \[\boxed{\begin{array}{c}\forall\epsilon>0,\thinspace\exists N\in\mathbb{N};\thinspace\forall\left(p,q\right)\in\mathbb{N}^{2},\\\left(p\geqslant N\text{ et }q\geqslant N\right)\Rightarrow d\left(u_{p},u_{q}\right)\leqslant\epsilon\end{array}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c93b8214278a0453c2212146fe5b3bcd_l3.png)
On peut montrer que :
![]()
Pour la réciproque de l’implication n° 2, c’est vite vu : il suffit de reprendre la suite réelle de terme général ![]() Cette suite est bornée mais n’est pas de Cauchy, puisque l’écart entre
Cette suite est bornée mais n’est pas de Cauchy, puisque l’écart entre ![]() et
et ![]() est égal à 2 lorsque
est égal à 2 lorsque ![]() sont de parités contraires (cet écart ne devient donc pas arbitrairement petit à partir d’un certain rang).
sont de parités contraires (cet écart ne devient donc pas arbitrairement petit à partir d’un certain rang).
Pour l’implication n° 1, c’est plus subtil. On ne pourra pas trouver de contre-exemple dans ![]() … car, comme on l’a admis dans cet article : toute suite réelle de Cauchy est convergente !
… car, comme on l’a admis dans cet article : toute suite réelle de Cauchy est convergente !
Un exemple de suite de Cauchy divergente
Notons ![]() l’espace vectoriel des applications continues de
l’espace vectoriel des applications continues de ![]() dans
dans ![]() .
.
Munissons ![]() de la « norme 1 » :
de la « norme 1 » :
![]()
![Rendered by QuickLaTeX.com \[f_{n}\left(t\right)=\left\{ \begin{array}{cc}1 & \text{si }t\in\left[0,\frac{1}{2}\right]\\\\0 & \text{si }t\in\left[\frac{1}{2}+\frac{1}{n},1\right]\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6d6afecd8d8b4fb67d657053305a4472_l3.png)
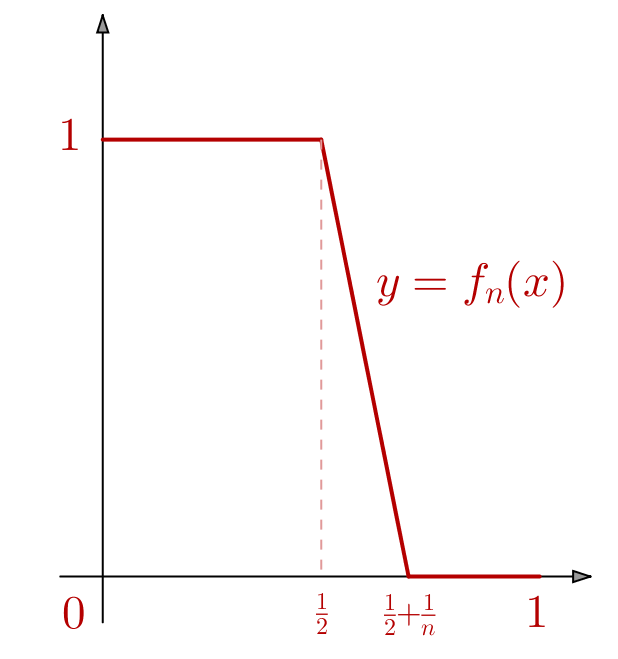
La suite ![]() est de Cauchy car si
est de Cauchy car si ![]() :
:
![Rendered by QuickLaTeX.com \[ \left\Vert f{q}-f_{p}\right\Vert =\int_{\frac{1}{2}}^{\frac{1}{2}+\frac{1}{p}}\,\left|f_{q}\left(t\right)-f_{p}\left(t\right)\right|\,dt\leqslant\frac{1}{p}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-be66ba72eb2af618bceac59e80f754bf_l3.png)
En effet, dans le cas contraire, en notant ![]() la limite, on aurait :
la limite, on aurait :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\,\left(\int_{0}^{\frac{1}{2}}\,\left|f\left(t\right)-1\right|\,dt+\int_{\frac{1}{2}}^{\frac{1}{2}+\frac{1}{n}}\,\left|f\left(t\right)-f_{n}\left(t\right)\right|\,dt+\int_{\frac{1}{2}+\frac{1}{n}}^{1}\,\left|f\left(t\right)\right|\,dt\right)=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d9b6c78449a90927444d3dae567db405_l3.png)
![Rendered by QuickLaTeX.com \[\int_{0}^{\frac{1}{2}}\,\left|f\left(t\right)-1\right|\,dt=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4c80b28a25c57adc752733728433f9f7_l3.png)
(![]() )
) ![]()
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\,\int_{\frac{1}{2}+\frac{1}{n}}^{1}\,\left|f\left(t\right)\right|\,dt=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e567edb93a2a3d4456473221afcd26d8_l3.png)
![Rendered by QuickLaTeX.com \[\int_{\frac{1}{2}}^{1}\,\left|f\left(t\right)\right|\,dt=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-76db892617c1e31ea3dbc2916a1e839e_l3.png)
(![]() )
) ![]()
Définition
L’espace métrique ![]() est dit complet si toutes ses suites de Cauchy convergent.
est dit complet si toutes ses suites de Cauchy convergent.
Ainsi ![]() est complet pour la distance usuelle (valeur absolue de la différence).
est complet pour la distance usuelle (valeur absolue de la différence).
Tout ![]() espace vectoriel normé
espace vectoriel normé ![]() (
(![]() evn en abrégé) est, de façon naturelle, un espace métrique pour la distance induite par la norme :
evn en abrégé) est, de façon naturelle, un espace métrique pour la distance induite par la norme : ![]() On dit que
On dit que ![]() est un espace de Banach lorsqu’il est complet pour cette distance.
est un espace de Banach lorsqu’il est complet pour cette distance.

On peut montrer que tout ![]() espace vectoriel de dimension finie, muni d’une norme quelconque, est un espace de Banach. Quant aux espaces normés de dimension infinie, certains sont complets et d’autre pas. Nous n’approfondirons pas davantage ce vaste sujet, du moins pas dans cet article.
espace vectoriel de dimension finie, muni d’une norme quelconque, est un espace de Banach. Quant aux espaces normés de dimension infinie, certains sont complets et d’autre pas. Nous n’approfondirons pas davantage ce vaste sujet, du moins pas dans cet article.
6 – Le petit théorème de Baire
Dans cette section, on s’intéresse à un exemple de théorème qui repose principalement sur la complétude d’un espace métrique. Il s’agit d’une généralisation du célèbre théorème des segments emboîtés.
Théorème (des fermés emboîtés)
Soit ![]() un espace métrique complet et soit
un espace métrique complet et soit ![]() une suite décroissante de fermés non vides dont le diamètre tend vers 0.
une suite décroissante de fermés non vides dont le diamètre tend vers 0.
Alors ![]() est un singleton.
est un singleton.
Ce résultat est aussi connu sous le nom de « petit théorème de Baire » (pour le grand théorème de Baire, voir un autre article … à paraître).
Preuve (cliquer pour déplier / replier)
On construit une suite ![]() telle que
telle que ![]() C’est possible puisque chaque
C’est possible puisque chaque ![]() est non vide.
est non vide.
Comme la suite ![]() est décroissante (pour l’inclusion), alors pour tout
est décroissante (pour l’inclusion), alors pour tout ![]() la suite tronquée
la suite tronquée ![]() est à termes dans
est à termes dans ![]() Il en résulte :
Il en résulte :
- d’une part, que pour tout
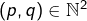 :
:
La suite![Rendered by QuickLaTeX.com \[q\geqslant p\Rightarrow d\left(x_{p},x_{q}\right)\leqslant\text{diam}\left(F_{p}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-60073c3f54118d61b23b2376aa253cc3_l3.png)
 est donc de Cauchy. Comme
est donc de Cauchy. Comme  est complet, elle converge. Notons
est complet, elle converge. Notons 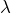 sa limite.
sa limite. - d’autre part que, pour tout
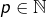 :
: 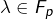 puisque
puisque 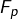 est fermé.
est fermé.
Ainsi :
![Rendered by QuickLaTeX.com \[\lambda\in\bigcap_{p=0}^{\infty}F_{p}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a947c50927bd3085c8e2a2a29e02f8c0_l3.png)
Pour finir, si ![]() appartient à cette intersection, alors pour tout
appartient à cette intersection, alors pour tout ![]() :
:
![]()
7 – Convergence absolue
Le résultat suivant concernant les séries numériques est fondamental :
Théorème
Soit ![]() une suite réelle. Si la série
une suite réelle. Si la série ![]() converge, alors la série
converge, alors la série ![]() converge aussi.
converge aussi.
Lorsque la série ![]() converge, la série
converge, la série ![]() est dite absolument convergente.
est dite absolument convergente.
Le théorème se reformule donc ainsi : toute série réelle absolument convergente est convergente.
Ce résultat est conséquence de la complétude de ![]()
Mais d’abord nous allons en donner une preuve qui, si l’on n’y prête pas garde, pourrait laisser croire le contraire.
Preuve 1 (cliquer pour déplier / replier)
Pour tout ![]() :
:
![]()
Cependant :
![]()
Comme la série ![]() converge, la principe de comparaison montre que la série
converge, la principe de comparaison montre que la série ![]() converge aussi.
converge aussi.
Finalement, la série ![]() converge, en tant que différence de deux séries convergentes.
converge, en tant que différence de deux séries convergentes.
Preuve 2 (cliquer pour déplier / replier)
Il s’agit de montrer que la suite de terme général 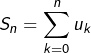 converge.
converge.
On sait, par hypothèse, que la suite de terme général 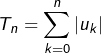 converge.
converge.
D’après l’inégalité triangulaire, pour tout ![]() tel que
tel que ![]() :
:
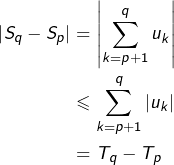
Or, étant donné ![]() il existe
il existe ![]() tel que pour tout
tel que pour tout ![]() et tout
et tout ![]() :
:
![]()
![]()
➡ La preuve 1 est indéniablement meilleure sur le plan de la concision. Elle présente, en outre, l’avantage d’être accessible, même si l’on ne dispose pas du critère de Cauchy.
Mais attention, cette preuve utilise le principe de comparaison pour les séries à termes positifs, qui repose sur le TLM, qui s’appuie à son tour sur le théorème de la borne supérieure, qui repose enfin sur le critère de Cauchy (ouf).
Donc, même si le critère de Cauchy n’apparaît pas explicitement dans la preuve 1, il est tout de même bien présent.
➡ Quant à la preuve 2, son intérêt est double :
- elle montre bien la connection entre suites de Cauchy et convergence absolue (sans rien camoufler),
- elle se généralise sans effort supplémentaire aux séries à termes dans un espace de Banach.
Revenons une dernière fois à l’exemple de la série 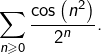
Il suffit, pour justifier sa convergence d’écrire que :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\;\left|\frac{\cos\left(n^{2}\right)}{2^{n}}\right|\leqslant\frac{1}{2^{n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fed7eab24a24d809fd95c1aa0baa8b19_l3.png)
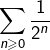 converge, le principe de comparaison assure que série
converge, le principe de comparaison assure que série 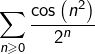 est absolument convergente, donc convergente.
est absolument convergente, donc convergente.
Pour conclure cette section, ajoutons qu’étant donné un ![]() -evn
-evn ![]() les assertions :
les assertions :
 est complet
est complet- dans
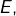 toute série ACV est convergente
toute série ACV est convergente
sont en fait équivalentes. Nous avons établi ci-dessus l’implication ![]() dans
dans ![]() . La preuve est en tout point identique dans un quelconque espace de Banach (on remplace simplement les valeurs absolues par des normes).
. La preuve est en tout point identique dans un quelconque espace de Banach (on remplace simplement les valeurs absolues par des normes).
Il suffit donc de prouver que ![]()
Proposition
Pour qu’un ![]() evn
evn ![]() soit complet, il suffit que toute série absolument convergente soit convergente.
soit complet, il suffit que toute série absolument convergente soit convergente.
Preuve (cliquer pour déplier / replier)
Notons ![]() la norme en vigueur dans
la norme en vigueur dans ![]() et soit
et soit ![]() une suite de Cauchy. On peut construire par récurrence une application
une suite de Cauchy. On peut construire par récurrence une application ![]() strictement croissante telle que :
strictement croissante telle que :
![]()
Comme la série ![]() converge, alors la série
converge, alors la série ![]() est absolument convergente, donc convergente. Mais cela signifie que la suite de terme général :
est absolument convergente, donc convergente. Mais cela signifie que la suite de terme général :
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n-1}\left(u_{\varphi\left(k+1\right)}-u_{\varphi\left(k\right)}\right)=u_{\varphi\left(n\right)}-u_{\varphi\left(0\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-edea31374a3053c15105cf5fca59f248_l3.png)
Etant donné ![]() , il existe
, il existe ![]() tel que
tel que
![]()
![]()
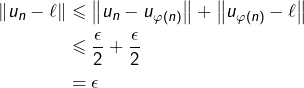
Remarque
On a montré au passage que toute suite de Cauchy possédant une valeur d’adhérence est convergente.
8 – Théorème de la projection orthogonale
L’objectif de cette section est d’établir le :
Théorème
Soit ![]() un espace de Hilbert réel (c’est-à-dire un espace vectoriel réel, muni d’un produit scalaire et complet pour la norme associée) et soit
un espace de Hilbert réel (c’est-à-dire un espace vectoriel réel, muni d’un produit scalaire et complet pour la norme associée) et soit ![]() une partie convexe, non vide et fermée de
une partie convexe, non vide et fermée de ![]()
Alors, pour tout ![]() il existe un unique
il existe un unique ![]() tel que :
tel que :
![]()
![]()
Comme ![]() alors
alors ![]() est une partie non vide et minorée de
est une partie non vide et minorée de ![]() qui admet donc une borne inférieure, notée
qui admet donc une borne inférieure, notée ![]()
Etant donné ![]() on peut associer à tout
on peut associer à tout ![]() un vecteur
un vecteur ![]() tel que :
tel que :
(![]() )
) ![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\left\Vert a_{p}-a_{q}\right\Vert \leqslant\sqrt{\frac{4d}{p}+\frac{4d}{q}+\frac{d}{p^{2}}+\frac{d}{q^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a6bc3aced6eddd499a58dd5a0012219a_l3.png)
![Rendered by QuickLaTeX.com \[\left\Vert a_{p}-a_{q}\right\Vert \leqslant\sqrt{\frac{10d}{p}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-99cd05b90f2652ae478ce6c6c2688d05_l3.png)
En passant à la limite dans l’encadrement ![]() on obtient (par continuité de la norme) :
on obtient (par continuité de la norme) : ![]()
Prouvons l’unicité. Soit ![]() tel que
tel que ![]() Toujours avec la formule du parallélogramme, il vient :
Toujours avec la formule du parallélogramme, il vient :
![]()
Passons pour finir à la caractérisation de ![]() Pour tout
Pour tout ![]() et pour tout
et pour tout ![]() le vecteur
le vecteur ![]() appartient à
appartient à ![]() et donc :
et donc :
![]()
![]()
![]()
(![]() )
) ![]()
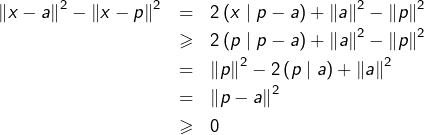
Annexe – Preuve du théorème de la borne supérieure
On commence par définir la notion de couple d’ensembles adjacents.
Définition
Soient ![]() des parties non vides de
des parties non vides de ![]()
On dit que ![]() est un couple d’ensembles adjacents lorsque :
est un couple d’ensembles adjacents lorsque :
(1) ![]()
(2) ![]()
Lemme
Si ![]() est un couple d’ensembles adjacents, alors il existe un unique
est un couple d’ensembles adjacents, alors il existe un unique ![]() tel que :
tel que :
![]()
Preuve (cliquer pour déplier / replier)
Commençons par l’unicité.
S’il existait deux réels ![]() ayant la propriété annoncée, on aurait pour tout
ayant la propriété annoncée, on aurait pour tout ![]() :
: ![]() ce qui est en contradiction avec (2).
ce qui est en contradiction avec (2).
Passons à l’existence de ![]()
D’après (2), il existe pour tout ![]() un couple
un couple ![]() tel que
tel que
(3) ![]()
![]()
![]()
![]()
La suite ![]() est donc de Cauchy. Notons
est donc de Cauchy. Notons ![]() sa limite.
sa limite.
D’après (3), la suite ![]() converge aussi vers
converge aussi vers ![]()
Soit ![]() comme
comme ![]() pour tout
pour tout ![]() il vient en passant à la limite :
il vient en passant à la limite : ![]()
On voit de même que pour tout ![]()
![]()
On est maintenant en mesure d’établir le :
Théorème (de la borne supérieure)
Toute partie non vide et majorée de ![]() possède une borne supérieure.
possède une borne supérieure.
Preuve (cliquer pour déplier / replier)
Soit ![]() une partie de
une partie de ![]() , non vide et majorée. Notons
, non vide et majorée. Notons ![]() l’ensemble de ses majorants :
l’ensemble de ses majorants :
![]()
Fixons ![]() et
et ![]() Soit
Soit ![]() Comme
Comme ![]() on voit déjà que
on voit déjà que ![]() D’autre part, si
D’autre part, si ![]() alors
alors ![]() et donc :
et donc :
![]()
![]()
![]()
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Ajout dans mon message précédent:
(…) certains en « déduisent » de façon erronée (…)
petite remarque pour un choix ( legerement 🙂 ) plus passionnant dans la section point fixe de Picard. Iterer sur une fonction (meme continue) ne garantit pas la convergence d’une suite recurrente. Exemple t -> 1-t sur [0 1/2[ U ]1/2 1] qui donne en effet deux valeurs selon parite’ de n… Et comme indique’, la convergence (ou pas) peut dependre de la condition initiale s. En reprenant la meme fonction avec s = 1/2 on a alors une suite constante (moins ennuyante que t -> t) donc convergente. Cela montre la convergence ou divergence de la meme fonction selon choix initial.
Serais-je à nouveau confus ?
Dans la section TLM : « Par exemple, la suite de terme général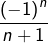 converge vers 0, mais n’est monotone à partir d’aucun rang ».
converge vers 0, mais n’est monotone à partir d’aucun rang ».
Monotone APCR ? Elle semble oscillante indéfiniment. D’accord sur sa limite égale à zéro.
Il est écrit que cette suite n’est monotone à partir d’aucun rang, ce qui signifie exactement qu’elle n’est PAS monotone APCR. Nous sommes donc bien d’accord 🙂
correction de mon nom.
OMG! je perds aussi mo focus en lisant en Franc,ais… Je commenc,ais a` perdre mon latin!
Merci bien de votre reponse… j’entends bien, dois me reconcentrer sur cette section. Y a t’il une demonstration sur Math-OS de la reciproque du critere de Cauchy? Je suis tres curieux de la comprendre. Intuitivement, cela parait evident, juste par un trace’ d’une suite qui converge, on peut comprendre pourquoi une suite de Cauchy converge sans en connaitre la limite.
Non, il n’y a pas de preuve de cette implication sur Math-OS. Ce n’est facile d’accès car il faut pour cela construire, d’une façon ou d’une autre, le corps des réels. Par exemple comme le quotient de l’anneau des suites de Cauchy de rationnels par l’idéal formé de celles qui convergent vers 0. Et seulement ensuite, on peut montrer la complétude de . Je vous renvoie par exemple au livre : Traité de mathématiques spéciales, de Ramis, Deschamps & Odoux, Tome 3, chapitre 1.
. Je vous renvoie par exemple au livre : Traité de mathématiques spéciales, de Ramis, Deschamps & Odoux, Tome 3, chapitre 1.
Bonjour – pour le critere de Cauchy, (reciproque de toute suite convergente est « de Cauchy »). Si on choisit L la limite de U comme etant le min_(|Up|, |Uq|) et le terme de rang k = (p ou q), Uk = Max_(|Up|, |Uq|). N’a t’on pas prouve’ la convergence de U vers L? Cela me parait trop simple et je me pose la question quant a` l’unicite de ce L. Quoique p et q etant fixe’s, L serait ainsi unique?
Il faut considerer la monotonie de U. e.g. si U est croissante, on choisit Max_(|Up|, |Uq|) = L (la limite de U) et Uk = min_(|Up|, |Uq|) et pour le cas precedent si U est decroissante.
Bonsoir,
Merci pour cet article.
Juste deux petites remarques (clairement 😊) non essentielles:
1) Au tout début de la partie 4, on peut ajouter « strictement positif » à la place de « positif »;
2) Parfois, une suite de Cauchy est définie de façon totalement équivalente à la définition de l’article, mais avec « n+p et n » en lieu et place de « p et q ». Il me semble qu’à partir de cette « variante », certains en déduisent le résultat faux que vous dénoncez dans votre aparté « confusion fréquente » de la partie 2. Je dis cela juste au cas où connaître la source probable de leur erreur, aiderait certains à ne plus la commettre !
Bien à vous.
Bien vu pour le _strictement_ positif ! En effet, on ne risque pas de converger vers 1 en itérant la fonction racine carrée à partir de 0 🙂
J’ai fait la rectification qui s’imposait.
Je crains que quelque chose ne vous ait échappé. Qu’entendez-vous par « le min de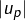 et
et 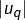 » ? La limite d’une suite, si elle existe, ne doit dépendre de RIEN d’autre que de cette suite … Et pour une suite à termes négatifs, ce nombre L serait donc positif ou nul ? Cela paraît difficile. En outre, vous semblez suggérer qu’une suite réelle doive nécessairement être soit croissante soit décroissante … C’est loin d’être vrai.
» ? La limite d’une suite, si elle existe, ne doit dépendre de RIEN d’autre que de cette suite … Et pour une suite à termes négatifs, ce nombre L serait donc positif ou nul ? Cela paraît difficile. En outre, vous semblez suggérer qu’une suite réelle doive nécessairement être soit croissante soit décroissante … C’est loin d’être vrai.