Dans cet article, on présente une jolie méthode (parmi tant d’autres …) pour établir :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\int_{0}^{+\infty}\dfrac{\sin\left(t\right)}{t}\thinspace dt=\dfrac{\pi}{2}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d66d8701009bfb392679fa0038fb62dc_l3.png)
Une fois n’est pas coutume, le texte est organisé à la manière d’une question d’oral (niveau X / ENS) ou disons, plutôt, d’un mini-problème en huit questions.
ÉNONCÉ
Dans ce qui suit, on pose pour tout réel 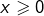 :
:
![Rendered by QuickLaTeX.com \[F\left(x\right)=\int_{0}^{+\infty}\dfrac{e^{-xt}}{1+t^{2}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d88b3708f65ec9595b7b3ebc4031cd16_l3.png)
1°) Montrer que  est bien définie sur
est bien définie sur 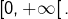
2°) Calculer 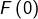 ainsi que
ainsi que 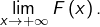
3°) Montrer que  est continue sur
est continue sur 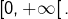
4°) Montrer que  est de classe
est de classe 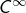 sur
sur ![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png) et qu’on peut dériver à tout ordre sous le signe somme.
et qu’on peut dériver à tout ordre sous le signe somme.
5°) Calculer, pour tout 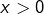 :
: 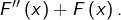
6°) Etant donnés un intervalle 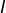 (non trivial), un réel
(non trivial), un réel 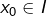 et une application
et une application 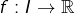 continue, vérifier que l’application :
continue, vérifier que l’application :
![Rendered by QuickLaTeX.com \[\Phi:I\rightarrow\mathbb{R},\thinspace x\mapsto\int_{x_{0}}^{x}f\left(t\right)\thinspace\sin\left(x-t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ee9ea21e83aaf98ec475c99965b18407_l3.png)
est une solution sur
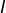
de l’équation différentielle
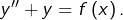
7°) En déduire que :
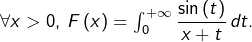
8°) Montrer, à l’aide de ce qui précède, que :
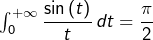
SOLUTION PROPOSÉE
Soit 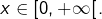 Pour tout
Pour tout 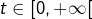 :
:
![Rendered by QuickLaTeX.com \[0\leqslant\dfrac{e^{-xt}}{1+t^{2}}\leqslant\dfrac{1}{1+t^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-12b995d8623a240350ff0ab128ca7bef_l3.png)
Or l’intégrale impropre
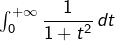
est convergente et donc, d’après le
principe de comparaison, il en va de même pour l’intégrale impropre
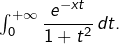
Ainsi, la fonction

est bien définie sur
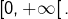
Le calcul de 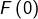 ne présente pas de difficulté :
ne présente pas de difficulté :
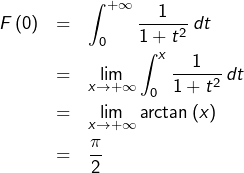
Par ailleurs, pour tout
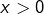
:
![Rendered by QuickLaTeX.com \[0\leqslant F\left(x\right)\leqslant\int_{0}^{+\infty}e^{-xt}\thinspace dt=\left[-\dfrac{1}{x}\thinspace e^{-xt}\right]_{t=0}^{+\infty}=\dfrac{1}{x} \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7751133597816baca3263d13ebe7e056_l3.png)
et d’après cet encadrement :
![Rendered by QuickLaTeX.com \[\lim_{x\rightarrow+\infty}F\left(x\right)=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2cc70abc95a085a578a69d54a2736f8c_l3.png)
Montrons que  est continue sur
est continue sur 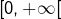 en nous appuyant sur le théorème de continuité des intégrales à paramètre, tel qu’il figure au programme officiel des filières MP / MPI. Notons :
en nous appuyant sur le théorème de continuité des intégrales à paramètre, tel qu’il figure au programme officiel des filières MP / MPI. Notons :
![Rendered by QuickLaTeX.com \[u:\left[0,+\infty\right[^{2}\rightarrow\mathbb{R},\thinspace\left(x,t\right)\mapsto\dfrac{e^{-xt}}{1+t^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8d348b1642d75ef3e1896b3d21d497c5_l3.png)
Pour tout
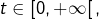
l’application partielle
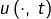
est continue. Pour tout
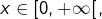
l’application partielle
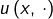
est continue (donc continue par morceaux) et de plus :
![Rendered by QuickLaTeX.com \[\forall\left(x,t\right)\in\left[0,+\infty\right[^{2},\thinspace\left|u\left(x,t\right)\right|=\dfrac{e^{-xt}}{1+t^{2}}\leqslant\dfrac{1}{1+t^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-586e4132f33f6856d563656f2f10020e_l3.png)
Comme l’application
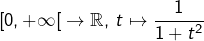
est intégrable, le théorème en question s’applique :

est continue sur
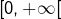
(et notamment en
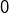
: ce point précis est crucial pour la suite).
Remarque
On peut montrer la continuité de  de façon élémentaire, comme dans cette vidéo :
de façon élémentaire, comme dans cette vidéo :
Montrons que, pour tout 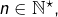
 est de classe
est de classe 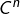 sur
sur ![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png) et que :
et que :
![Rendered by QuickLaTeX.com \[\forall x>0,\thinspace F^{\left(n\right)}\left(x\right)=\int_{0}^{+\infty}\dfrac{\left(-1\right)^{n}t^{n}e^{-xt}}{1+t^{2}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a556a469580cedb6ce5cbcd9695cb8f4_l3.png)
On raisonne par récurrence en commençant par
Soit  Notons
Notons  et considérons l’application
et considérons l’application
![Rendered by QuickLaTeX.com \[u:A\times\left[0,+\infty\right[\rightarrow\mathbb{R},\thinspace\left(x,t\right)\mapsto\dfrac{e^{-xt}}{1+t^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-385b33a0d265476c3151aa266c968829_l3.png)
Pour tout
l’application partielle
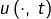
est de classe
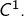
Pour tout
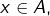
l’application partielle
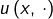
est intégrable. Pour tout
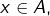
la dérivée partielle
![Rendered by QuickLaTeX.com \[\partial_{1}u\left(x,\thinspace\cdot\right):\left[0,+\infty\right[\rightarrow\mathbb{R},\thinspace t\mapsto-\dfrac{t\thinspace e^{-xt}}{1+t^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-17754bccd18f8d093b59e6393b7ff9df_l3.png)
est (largement …) continue par morceaux. Enfin :
![Rendered by QuickLaTeX.com \[\forall x\in A,\thinspace\forall t\in\left[0,+\infty\right[,\thinspace\left|\partial_{1}u\left(x,t\right)\right|\leqslant\dfrac{t\thinspace e^{-at}}{1+t^{2}}\leqslant t\thinspace e^{-at}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f06306644d52d70e307299993502ffa2_l3.png)
et l’application
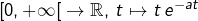
est intégrable. Le théorème de dérivation des intégrales à paramètre s’applique :

est de classe
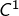
(sur
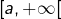
pour tout
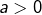
et donc sur)
![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png)
et :
![Rendered by QuickLaTeX.com \[\forall x>0,\thinspace F'\left(x\right)=\int_{0}^{+\infty}\dfrac{-t\thinspace e^{-xt}}{1+t^{2}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a552998b1bae77125be5c801d85a2d06_l3.png)
Supposons que, pour un certain 
 soit de classe
soit de classe 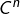 sur
sur ![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png) et que :
et que :
![Rendered by QuickLaTeX.com \[\forall x>0,\thinspace F^{\left(n\right)}\left(x\right)=\int_{0}^{+\infty}\dfrac{\left(-1\right)^{n}t^{n}\thinspace e^{-xt}}{1+t^{2}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-94e0499bf5c097313178ef11a93e7825_l3.png)
On refait essentiellement la même chose qu’au a), mais avec l’application
![Rendered by QuickLaTeX.com \[u_{n}:A\times\left[0,+\infty\right[\rightarrow\mathbb{R},\thinspace\left(x,t\right)\mapsto\dfrac{\left(-1\right)^{n}t^{n}\thinspace e^{-xt}}{1+t^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f319b70178b2606c202980853ea38feb_l3.png)
On montre ainsi que
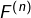
est de classe
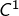
sur
![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png)
(autrement dit que

est de classe
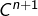
sur cet intervalle) et que :
![Rendered by QuickLaTeX.com \[\forall x>0,\thinspace F^{\left(n+1\right)}\left(x\right)=\int_{0}^{+\infty}\partial_{1}u_{n}\left(x,t\right)\thinspace dt=\int_{0}^{+\infty}\dfrac{\left(-1\right)^{n+1}t^{n+1}\thinspace e^{-xt}}{1+t^{2}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-92c35db1f4cfc70d0b1ab1d90ccb57ce_l3.png)
Question 5°)
Pour tout 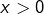 :
:
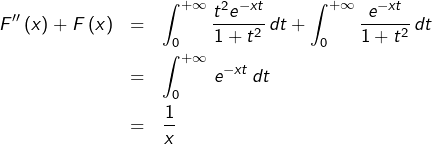
Autrement dit,

est solution sur
![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png)
de l’équation différentielle (linéaire du second ordre et à coefficients constants) :
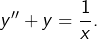
Grâce à la formule d’addition du sinus, on voit que pour tout 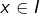 :
:
![Rendered by QuickLaTeX.com \[\Phi\left(x\right)=\sin\left(x\right)C\left(x\right)-\cos\left(x\right)S\left(x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0ea500f3e87cc4a99e4290ec92788fd6_l3.png)
où l’on a posé :
![Rendered by QuickLaTeX.com \[C\left(x\right)=\int_{x_{0}}^{x}\thinspace f\left(t\right)\cos\left(t\right)\thinspace dt\qquad\text{et}\qquad S\left(x\right)=\int_{x_{0}}^{x}\thinspace f\left(t\right)\sin\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7fec0fb21b9eece9d5336651c8bebcf3_l3.png)
On calcule alors successivement :
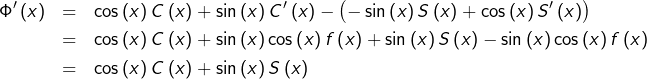
puis :
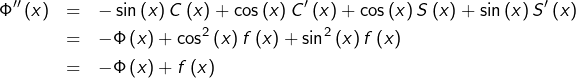
Ceci prouve que

est une solution sur
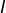
de
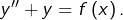
Il s’agit de l’unique solution sur
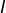
de cette équation différentielle, qui s’annule en
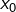
et dont la dérivée s’annule aussi en ce point.
Question 7°)
Notons 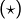 l’équation différentielle :
l’équation différentielle :
![Rendered by QuickLaTeX.com \[y''+y=\dfrac{1}{x}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2dd41f56a1f41a8d0260829432833417_l3.png)
D’après 6°, étant donné
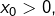
l’application :
![Rendered by QuickLaTeX.com \[\left]0,+\infty\right[\rightarrow\mathbb{R},\thinspace x\mapsto\int_{x_{0}}^{x}\dfrac{\sin\left(x-t\right)}{t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cae454b449d8fe9e87c9f7e5e9384bef_l3.png)
est une solution sur
![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png)
de
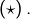
En lui ajoutant n’importe quelle combinaison linéaire de
et
on obtient encore une solution. Considérons l’application :
![Rendered by QuickLaTeX.com \[G:\left]0,+\infty\right[\rightarrow\mathbb{R},\thinspace x\mapsto\int_{x}^{+\infty}\dfrac{\sin\left(t-x\right)}{t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-eec2b30abf8c815548a27e1e8b7c2e2e_l3.png)
La relation de Chasles donne, pour tout
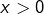
:
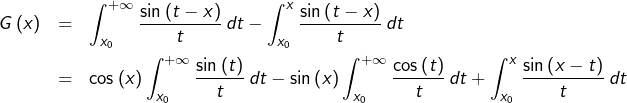
Par conséquent,
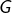
est solution sur
![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png)
de
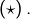
Or, on a vu au 5°) que c’est aussi le cas de
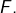
Il s’ensuit que
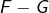
est solution sur
![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png)
de
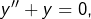
d’où l’existence de réels
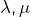
tels que :
![Rendered by QuickLaTeX.com \[\forall x>0,\thinspace F\left(x\right)-G\left(x\right)=\lambda\cos\left(x\right)+\mu\sin\left(x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b277876de2d7a278d03835398d042c7b_l3.png)
Maintenant on sait (cf. 2°) que
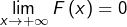
et il est facile de voir que
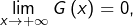
puisque pour tout
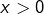
:
![Rendered by QuickLaTeX.com \[G\left(x\right)=\cos\left(x\right)\underbrace{\int_{x}^{+\infty}\dfrac{\sin\left(t\right)}{t}\thinspace dt}_{\underset{x\rightarrow+\infty}{\longrightarrow}0}-\sin\left(x\right)\underbrace{\int_{x}^{+\infty}\dfrac{\cos\left(t\right)}{t}\thinspace dt}_{\underset{x\rightarrow+\infty}{\longrightarrow}0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aabbb0c076a3c8deea442af7c11431b0_l3.png)
Ainsi
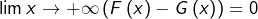
et ceci impose
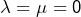
(pour le détail de cette dernière affirmation, voir
l’annexe 1). Moralité :
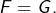
Et pour finir, en posant
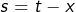
dans l’intégrale qui définit
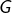
:
![Rendered by QuickLaTeX.com \[\boxed{\forall x>0,\thinspace F\left(x\right)=\int_{0}^{+\infty}\dfrac{\sin\left(s\right)}{x+s}\thinspace ds}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d0b80ab822ca83d495417247e72cb6ed_l3.png)
Question 8°)
On aimerait bien remplacer  par
par 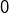 dans l’égalité ci-dessus, mais ce n’est pas possible !… En revanche, on peut s’en sortir en faisant tendre
dans l’égalité ci-dessus, mais ce n’est pas possible !… En revanche, on peut s’en sortir en faisant tendre  vers
vers 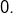 Ce qui précède montre que, pour tout
Ce qui précède montre que, pour tout 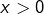 :
:
![Rendered by QuickLaTeX.com \[\int_{0}^{+\infty}\dfrac{e^{-xt}}{1+t^{2}}\thinspace dt=\cos\left(x\right)\int_{x}^{+\infty}\dfrac{\sin\left(t\right)}{t}\thinspace dt-\sin\left(x\right)\int_{x}^{+\infty}\dfrac{\cos\left(t\right)}{t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0a819fcaffeef9952c3486cc3fd0271d_l3.png)
Lorsque

tend vers
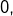
le membre de gauche tend vers
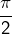
(par continuité de

en
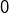
: cf. question 3°). Comme l’intégrale impropre
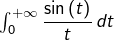
est convergente (non détaillé ici : c’est la fameuse intégrale de Dirichlet), on a par ailleurs :
![Rendered by QuickLaTeX.com \[\lim_{x\rightarrow0}\left[\cos\left(x\right)\int_{x}^{+\infty}\dfrac{\sin\left(t\right)}{t}\thinspace dt\right]=\int_{0}^{+\infty}\dfrac{\sin\left(t\right)}{t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3ce7f9ac3134c9ecfffbc53ec39fcdff_l3.png)
Il reste donc à prouver que :
![Rendered by QuickLaTeX.com \[\lim_{x\rightarrow0}\left[\sin\left(x\right)\int_{x}^{+\infty}\dfrac{\cos\left(t\right)}{t}\thinspace dt\right]=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-939ebf939e5206667ee97877cc26fd36_l3.png)
ce qui donnera la conclusion. Or :
![Rendered by QuickLaTeX.com \[\dfrac{\cos\left(t\right)}{t}\underset{{\scriptstyle 0}}{\sim}\dfrac{1}{t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-94b9e00ea324f45abe0e1a6559c0f047_l3.png)
donc, d’après le théorème de sommation des relations de comparaison (cas des intégrales impropres divergentes de fonction positives) :
![Rendered by QuickLaTeX.com \[\int_{x}^{1}\dfrac{\cos\left(t\right)}{t}\thinspace dt\underset{{\scriptstyle 0}}{\sim}\int_{x}^{1}\dfrac{1}{t}\thinspace dt=-\ln\left(x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6d9ea46805d83a5a899f4dbfdfdc2dc0_l3.png)
et donc :
![Rendered by QuickLaTeX.com \[\int_{x}^{+\infty}\dfrac{\cos\left(t\right)}{t}\thinspace dt\underset{{\scriptstyle 0}}{\sim}-\ln\left(x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-83345b5f097c813912c6d6eb1d931526_l3.png)
d’où finalement :
![Rendered by QuickLaTeX.com \[\sin\left(x\right)\int_{x}^{+\infty}\dfrac{\cos\left(t\right)}{t}\thinspace dt\underset{{\scriptstyle 0}}{\sim}-x\ln\left(x\right)\underset{x\rightarrow0}{\longrightarrow}0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e73056b840ec423bd1c3059f9d2771b8_l3.png)
ANNEXE 1
Etant donnés 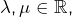 considérons l’application :
considérons l’application :
![Rendered by QuickLaTeX.com \[\theta:\left]0,+\infty\right[\rightarrow\mathbb{R},\thinspace x\mapsto\lambda\cos\left(x\right)+\mu\sin\left(x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-73e655171714a4959c65dc6b6b541b70_l3.png)
A la question 7°, on s’est servi du fait que si
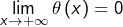
alors
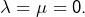
Prouvons cela par l’absurde.
Supposons 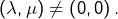 Alors pour tout
Alors pour tout 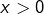 :
:
![Rendered by QuickLaTeX.com \[\theta\left(x\right)=\sqrt{\lambda^{2}+\mu^{2}}\thinspace\left[\dfrac{\lambda}{\sqrt{\lambda^{2}+\mu^{2}}}\cos\left(x\right)+\dfrac{\mu}{\sqrt{\lambda^{2}+\mu^{2}}}\sin\left(x\right)\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5e99583e8ae52bcdc706a322184ec1b4_l3.png)
Comme :
![Rendered by QuickLaTeX.com \[\left(\dfrac{\lambda}{\sqrt{\lambda^{2}+\mu^{2}}}\right)^{2}+\left(\dfrac{\mu}{\sqrt{\lambda^{2}+\mu^{2}}}\right)^{2}=1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-69746c572c04f02a5a4e97fe9953469b_l3.png)
il existe

tel que :
![Rendered by QuickLaTeX.com \[\dfrac{\lambda}{\sqrt{\lambda^{2}+\mu^{2}}}=\cos\left(x_{0}\right)\qquad\text{et}\qquad\dfrac{\mu}{\sqrt{\lambda^{2}+\mu^{2}}}=\sin\left(x_{0}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5fa0fe9bc3d0bf234950b6baa8f52d74_l3.png)
Ainsi, pour tout
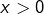
:
![Rendered by QuickLaTeX.com \[\theta\left(x\right)=\sqrt{\lambda^{2}+\mu^{2}}\thinspace\cos\left(x-x_{0}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1ad61940c742cd48f9c868af722f0491_l3.png)
et en particulier, pour tout
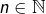
:
![Rendered by QuickLaTeX.com \[\theta\left(x_{0}+2n\pi\right)=\sqrt{\lambda^{2}+\mu^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-14f39d1200d42059f50685f8307680c6_l3.png)
ce qui contredit l’hypothèse
ANNEXE 2
Dans cette vidéo, on signale sans démonstration que l’application :
![Rendered by QuickLaTeX.com \[F:\left[0,+\infty\right[\rightarrow\mathbb{R},\thinspace x\mapsto\int_{0}^{+\infty}\dfrac{e^{-xt}}{1+t^{2}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-123b7417f84b8b31f12c54ecc636bc61_l3.png)
est dérivable sur
![Rendered by QuickLaTeX.com \left]0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-90d2d03eec9a031b0d2601b2f615f2df_l3.png)
et que :
![Rendered by QuickLaTeX.com \[\forall x>0,\thinspace F'\left(x\right)=-\int_{0}^{+\infty}\thinspace\dfrac{t\thinspace e^{-xt}}{1+t^{2}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8090ef791f20af65695680fd18dc5ce2_l3.png)
L’objet de cette annexe est d’en fournir une preuve « élémentaire », qui ne repose PAS sur le théorème de dérivabilité des intégrales à paramètres (lequel repose à son tour sur le théorème de convergence dominée de Lebesgue). On s’appuiera notamment sur le résultat suivant :
On note déjà que 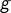 est continue (c’est la limite uniforme d’une suite d’applications continues). Comme les
est continue (c’est la limite uniforme d’une suite d’applications continues). Comme les 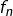 sont de classe
sont de classe 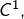 on a pour tout
on a pour tout 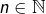 et pour tout
et pour tout 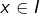 :
:
![Rendered by QuickLaTeX.com \[f_{n}\left(x\right)=f_{n}\left(x_{0}\right)+\int_{x_{0}}^{x}\thinspace f_{n}'\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-964b977400d074575bd3c11e61096a71_l3.png)
Donc, vue l’hypothèse de convergence uniforme :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}f_{n}\left(x\right)=\lambda+\int_{x_{0}}^{x}\thinspace g\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5c60fac40131ebb2112f75122977ebf9_l3.png)
Visiblement, la limite simple de la suite
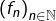
est de classe
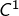
et sa dérivée est
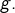
Remarque
En pratique, la convergence simple sur 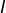 de la suite
de la suite 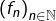 est généralement évidente. L’intérêt de cette proposition est alors de prouver que « la dérivée de la limite est égale à la lmite de la dérivée ».
est généralement évidente. L’intérêt de cette proposition est alors de prouver que « la dérivée de la limite est égale à la lmite de la dérivée ».
A présent, passons à la preuve du résultat annoncé.
Pour tout 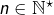 et pour tout
et pour tout 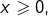 posons :
posons :
![Rendered by QuickLaTeX.com \[F_{n}\left(x\right)=\int_{0}^{n}\dfrac{e^{-xt}}{1+t^{2}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9af4bc65bfbde6bbefc01895b96ef600_l3.png)
On sait que la suite
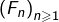
converge simplement sur
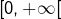
vers
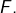
On va montrer successivement que :
pour tout 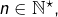
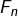 est de classe
est de classe 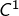 sur
sur 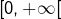 et sa dérivée est donnée par :
et sa dérivée est donnée par :
![Rendered by QuickLaTeX.com \[\forall x\geqslant0,\thinspace F_{n}'\left(x\right)=\int_{0}^{n}\dfrac{-t\thinspace e^{-xt}}{1+t^{2}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6c7f02fea6cd80118c93e240d8f05dc6_l3.png)
la suite 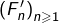 converge uniformément sur tout intervalle du type
converge uniformément sur tout intervalle du type 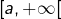 (avec
(avec 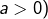 vers
vers
![Rendered by QuickLaTeX.com \[G:\left]0,+\infty\right[\rightarrow\mathbb{R},\thinspace x\mapsto\int_{0}^{+\infty}\dfrac{-t\thinspace e^{-xt}}{1+t^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c3b7cc146c35b20e9e62733d5f1e3b2c_l3.png)
ce qui permettra de conclure, d’après la proposition précédente.
➡ Pour le premier point, fixons 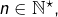
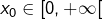 ainsi que
ainsi que 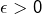 et prouvons qu’il existe
et prouvons qu’il existe 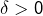 tel que pour tout
tel que pour tout 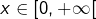 :
:
![Rendered by QuickLaTeX.com \[\left|x-x_{0}\right|\leqslant\delta\Rightarrow\left|F_{n}\left(x\right)-F_{n}\left(x_{0}\right)-\left(x-x_{0}\right)\int_{0}^{n}\dfrac{-t\thinspace e^{-x_{0}t}}{1+t^{2}}\thinspace dt\right|\leqslant\epsilon\left|x-x_{0}\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4240f30df68bfa561426813a368ebc45_l3.png)
Notons
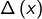
le membre de gauche de cette inégalité. On a :
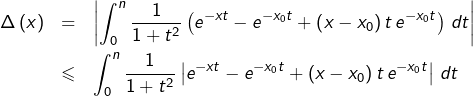
Notons
![Rendered by QuickLaTeX.com J=\left[x_{0}-1,x_{0}+1\right]\cap\left[0,+\infty\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-ce9031dcbd13f8ee52c5d51618b52a09_l3.png)
et
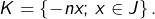
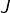 et
et 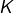 sont des segments. En posant
sont des segments. En posant 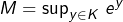 et d’après l’inégalité de Taylor à l’ordre 2 :
et d’après l’inégalité de Taylor à l’ordre 2 :
![Rendered by QuickLaTeX.com \[\forall\left(a,b\right)\in K^{2},\thinspace\left|e^{b}-e^{a}-\left(b-a\right)e^{a}\right|\leqslant M\thinspace\dfrac{\left(b-a\right)^{2}}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e6bffbf5eac2c418e09c4e91c5d7318f_l3.png)
donc :
![Rendered by QuickLaTeX.com \[\forall x\in J,\thinspace\forall t\in\left[0,n\right],\thinspace\left|e^{-xt}-e^{-x_{0}t}+\left(x-x_{0}\right)t\thinspace e^{-x_{0}t}\right|\leqslant M\thinspace\dfrac{\left(x-x_{0}\right)^{2}t^{2}}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-409e34c60766e400e7fbbc588a07d66c_l3.png)
Il s’ensuit que :
![Rendered by QuickLaTeX.com \[\forall x\in J,\thinspace\Delta\left(x\right)\leqslant\dfrac{M}{2}\left(x-x_{0}\right)^{2}\thinspace\int_{0}^{n}\thinspace\dfrac{t^{2}}{1+t^{2}}\thinspace dt\leqslant\dfrac{Mn}{2}\left(x-x_{0}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-628edfd6b3f27fa4cc657fde23239f7f_l3.png)
et donc, que si

est assez proche de
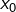
:
![Rendered by QuickLaTeX.com \[\Delta\left(x\right)\leqslant\epsilon\left|x-x_{0}\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-09c8481c83d150f10a7f9ee3923887bb_l3.png)
➡ Pour le second point, on observe que pour tout  tout
tout  et tout
et tout  :
:
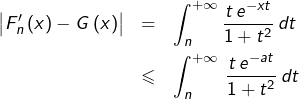
Or cette dernière quantité est indépendante de

et tend vers
lorsque

tend vers
La suite
converge donc bien uniformément vers
sur tout intervalle de la forme
avec

Pour toutes questions ou remarques, merci d’utiliser le formulaire de contact.
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\int_{0}^{+\infty}\dfrac{\sin\left(t\right)}{t}\thinspace dt=\dfrac{\pi}{2}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d66d8701009bfb392679fa0038fb62dc_l3.png)
![]()
![]()
![]()
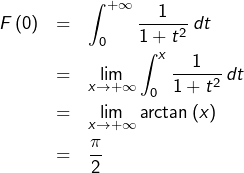
![Rendered by QuickLaTeX.com \[0\leqslant F\left(x\right)\leqslant\int_{0}^{+\infty}e^{-xt}\thinspace dt=\left[-\dfrac{1}{x}\thinspace e^{-xt}\right]_{t=0}^{+\infty}=\dfrac{1}{x} \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7751133597816baca3263d13ebe7e056_l3.png)
![]()
![]()
![]()
![]()
![]() Notons
Notons ![]() et considérons l’application
et considérons l’application![]()
![]()
![]()
![]()
![]()
![]() soit de classe
soit de classe ![]() sur
sur ![]() et que :
et que :![]()
![]()
![]()
![]() soit de classe
soit de classe ![]() sur
sur ![]() peut être établi SANS utiliser cette artillerie (qui repose sur le théorème de convergence dominée de Lebesgue … rien de trivial à l’horizon …). Voir l’annexe 2.
peut être établi SANS utiliser cette artillerie (qui repose sur le théorème de convergence dominée de Lebesgue … rien de trivial à l’horizon …). Voir l’annexe 2.![]() :
: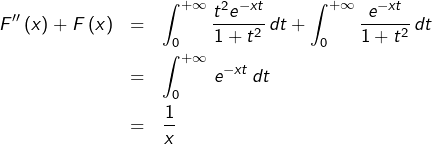
![]()
![]()
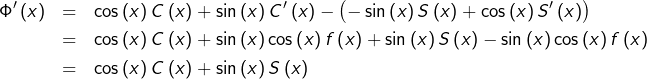
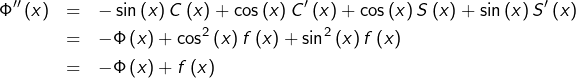
![]()
![]()
![]()
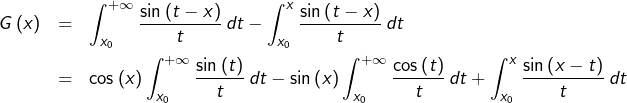
![]()
![Rendered by QuickLaTeX.com \[G\left(x\right)=\cos\left(x\right)\underbrace{\int_{x}^{+\infty}\dfrac{\sin\left(t\right)}{t}\thinspace dt}_{\underset{x\rightarrow+\infty}{\longrightarrow}0}-\sin\left(x\right)\underbrace{\int_{x}^{+\infty}\dfrac{\cos\left(t\right)}{t}\thinspace dt}_{\underset{x\rightarrow+\infty}{\longrightarrow}0}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aabbb0c076a3c8deea442af7c11431b0_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\forall x>0,\thinspace F\left(x\right)=\int_{0}^{+\infty}\dfrac{\sin\left(s\right)}{x+s}\thinspace ds}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d0b80ab822ca83d495417247e72cb6ed_l3.png)
![]() par
par ![]() dans l’égalité ci-dessus, mais ce n’est pas possible !… En revanche, on peut s’en sortir en faisant tendre
dans l’égalité ci-dessus, mais ce n’est pas possible !… En revanche, on peut s’en sortir en faisant tendre ![]() vers
vers ![]() Ce qui précède montre que, pour tout
Ce qui précède montre que, pour tout ![]() :
:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() considérons l’application :
considérons l’application :![]()
![]() Alors pour tout
Alors pour tout ![]() :
:![Rendered by QuickLaTeX.com \[\theta\left(x\right)=\sqrt{\lambda^{2}+\mu^{2}}\thinspace\left[\dfrac{\lambda}{\sqrt{\lambda^{2}+\mu^{2}}}\cos\left(x\right)+\dfrac{\mu}{\sqrt{\lambda^{2}+\mu^{2}}}\sin\left(x\right)\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5e99583e8ae52bcdc706a322184ec1b4_l3.png)
![Rendered by QuickLaTeX.com \[\left(\dfrac{\lambda}{\sqrt{\lambda^{2}+\mu^{2}}}\right)^{2}+\left(\dfrac{\mu}{\sqrt{\lambda^{2}+\mu^{2}}}\right)^{2}=1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-69746c572c04f02a5a4e97fe9953469b_l3.png)
![]()
![]()
![]()
![]()
![]()
![]() un intervalle (non trivial) et soit
un intervalle (non trivial) et soit ![]() une suite d’applications de classe
une suite d’applications de classe ![]() On suppose :
On suppose : tel que la suite
tel que la suite 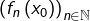 soit convergente (on note
soit convergente (on note 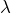 sa limite)
sa limite)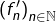 converge uniformément sur
converge uniformément sur 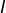 vers vers une application
vers vers une application 
![]() converge simplement sur
converge simplement sur ![]() vers une application
vers une application ![]() de classe
de classe ![]() et de plus
et de plus ![]()
![]()
![]()
![]()
![]()
![]()
![]()
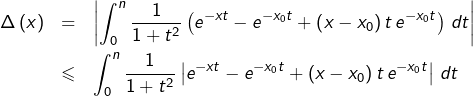
![]() et
et ![]() sont des segments. En posant
sont des segments. En posant ![]() et d’après l’inégalité de Taylor à l’ordre 2 :
et d’après l’inégalité de Taylor à l’ordre 2 :![]()
![]()
![]()
![]()
![]() tout
tout ![]() et tout
et tout ![]() :
: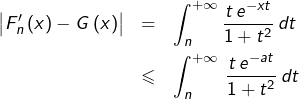



Pouvez-vous calculer l’intégrale ci-dessous, entre les bornes 2.5 et 4 en degrés de la fonction :
sin(x^((1+cos(x))^x))
soit, une fois décomposée :
1) 1+cos(x) = A
2) A^x = B [A élevé à la puissance x]
3) x^B = C
4) sin(C) la fonction finale
Cette question ne me semble pas en rapport avec l’article 🙂 En outre, je doute fort que l’on sache calculer exactement une telle intégrale. Toutefois, avec un logiciel approprié, on peut en déterminer une valeur approchée aussi précise qu’on le désire. En voici une, à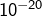 près : 1.26424035230572825036
près : 1.26424035230572825036