Neuf énoncés d’exercices sur les sommes de Riemann (fiche 02). La fiche 01 est ici.
Etant donné 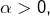 utiliser une somme de Riemann pour trouver un équivalent, lorsque
utiliser une somme de Riemann pour trouver un équivalent, lorsque 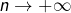 , de :
, de :
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=1}^{n}k^{\alpha}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b4de1b560d03ae20cadb40797bcf459a_l3.png)
Calculer 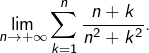
En utilisant une somme de Riemann, calculer 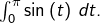
Dans l’exercice n° 6 de cette fiche, on établit la célèbre inégalité de Jensen « discrète » , dont l’énoncé est rappelé ci-dessous :
Théorème
Si 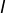 est un intervalle non trivial et si
est un intervalle non trivial et si 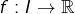 est convexe, alors :
est convexe, alors :
![Rendered by QuickLaTeX.com \[f\left(\sum_{i=1}^{n}t_{i}x_{i}\right)\leqslant\sum_{i=1}^{n}t_{i}\thinspace f\left(x_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-038569d4d96102ba9b789df2a6987325_l3.png)
pour tout

tout
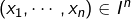
et tout
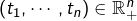
tel que
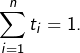
Montrer que si 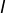 est un intervalle ouvert, si
est un intervalle ouvert, si ![Rendered by QuickLaTeX.com u:\left[a,b\right]\rightarrow I](https://math-os.com/wp-content/ql-cache/quicklatex.com-4693852b64c8c236b1af7c36453c2560_l3.png) est continue et si
est continue et si 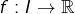 est convexe, alors (inégalité de Jensen « continue ») :
est convexe, alors (inégalité de Jensen « continue ») :
![Rendered by QuickLaTeX.com \[f\left(\dfrac{1}{b-a}\int_{a}^{b}\thinspace u\left(t\right)\thinspace dt\right)\leqslant\dfrac{1}{b-a}\int_{a}^{b}f\left(u\left(t\right)\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5dfad542cf2cf1d88b8bf9feb4b3a260_l3.png)
Soit ![Rendered by QuickLaTeX.com f:\left[0,1\right]\rightarrow\mathbb{R}](https://math-os.com/wp-content/ql-cache/quicklatex.com-24d21c2af9c99ccd14b07bf411b8970d_l3.png) de classe
de classe 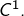 Montrer que :
Montrer que :
![Rendered by QuickLaTeX.com \[\frac{1}{n}\,\sum_{k=0}^{n-1}\,f\left(\frac{k}{n}\right)=\int_{0}^{1}\,f\left(t\right)\,dt-\frac{1}{2n}\,\left(f\left(1\right)-f\left(0\right)\right)+o\left(\frac{1}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ff9f4b14fc66e5c2a9b47e4bc1205278_l3.png)
Soient ![Rendered by QuickLaTeX.com f,g:\left[0,1\right]\rightarrow\mathbb{R}](https://math-os.com/wp-content/ql-cache/quicklatex.com-c1e59086c3878328334e2e25cceaa826_l3.png) des applications continues. Calculer :
des applications continues. Calculer :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\dfrac{1}{n}\sum_{k=1}^{n-1}f\left(\dfrac{k}{n}\right)\thinspace g\left(\dfrac{k+1}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-68f0d8dcaa8a50debbab05e0ee39ad65_l3.png)
Soit ![Rendered by QuickLaTeX.com f:\left[0,1\right]\rightarrow\mathbb{R}](https://math-os.com/wp-content/ql-cache/quicklatex.com-24d21c2af9c99ccd14b07bf411b8970d_l3.png) décroissante et convexe. On pose, pour tout
décroissante et convexe. On pose, pour tout 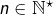 :
:
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{1}{n}\sum_{k=1}^{n}f\left(\dfrac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0ba3585cb6997761631e52d050054af9_l3.png)
Montrer que la suite
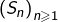
est croissante, puis donner un exemple montrant que, sans hypothèse de convexité, cette suite peut osciller.
Soit ![Rendered by QuickLaTeX.com f:\left[a,b\right]\rightarrow\mathbb{R}](https://math-os.com/wp-content/ql-cache/quicklatex.com-d4da71c7eb5c9e6aa61c58d77d717be2_l3.png) continue.
continue.
On subdivise le segment ![Rendered by QuickLaTeX.com \left[a,b\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c1c9b62f4ffe493505d6566104a9b311_l3.png) en posant, pour tout
en posant, pour tout 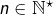 et pour tout
et pour tout 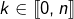 :
:
![Rendered by QuickLaTeX.com \[x_{k,n}=a+\frac{k}{n}\left(b-a\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9bc910574cc83d3e7036b13e83d38491_l3.png)
Calculer alors :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\sum_{k=0}^{n-1}\left|\int_{x_{k,n}}^{x_{k+1,n}}f\left(t\right)\thinspace dt\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d133ea7bcdb627210111c8d66883b313_l3.png)
On pose :
![Rendered by QuickLaTeX.com \[f:\left]0,1\right]\rightarrow\mathbb{R},\thinspace x\mapsto\dfrac{1}{x}\sin\left(\dfrac{1}{x}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b274d1b1941dececee0a91e65be75303_l3.png)
et pour tout
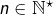
:
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{1}{n}\thinspace\sum_{k=1}^{n}f\left(\dfrac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9c2d5b8fbd0fbb04d5ea0e31e7fd0213_l3.png)
- Montrer que l’intégrale
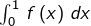 est convergente.
est convergente.
- Montrer que la suite
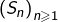 est divergente.
est divergente.
- Commenter, en faisant le lien avec l’exercice n° 8 de cette fiche
Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=1}^{n}k^{\alpha}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b4de1b560d03ae20cadb40797bcf459a_l3.png)
![Rendered by QuickLaTeX.com \[f\left(\sum_{i=1}^{n}t_{i}x_{i}\right)\leqslant\sum_{i=1}^{n}t_{i}\thinspace f\left(x_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-038569d4d96102ba9b789df2a6987325_l3.png)
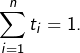
![]()
![Rendered by QuickLaTeX.com \[\frac{1}{n}\,\sum_{k=0}^{n-1}\,f\left(\frac{k}{n}\right)=\int_{0}^{1}\,f\left(t\right)\,dt-\frac{1}{2n}\,\left(f\left(1\right)-f\left(0\right)\right)+o\left(\frac{1}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ff9f4b14fc66e5c2a9b47e4bc1205278_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\dfrac{1}{n}\sum_{k=1}^{n-1}f\left(\dfrac{k}{n}\right)\thinspace g\left(\dfrac{k+1}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-68f0d8dcaa8a50debbab05e0ee39ad65_l3.png)
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{1}{n}\sum_{k=1}^{n}f\left(\dfrac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0ba3585cb6997761631e52d050054af9_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\sum_{k=0}^{n-1}\left|\int_{x_{k,n}}^{x_{k+1,n}}f\left(t\right)\thinspace dt\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d133ea7bcdb627210111c8d66883b313_l3.png)
![]()
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{1}{n}\thinspace\sum_{k=1}^{n}f\left(\dfrac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9c2d5b8fbd0fbb04d5ea0e31e7fd0213_l3.png)
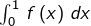 est convergente.
est convergente.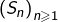 est divergente.
est divergente.![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=1}^{n}k^{\alpha}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b4de1b560d03ae20cadb40797bcf459a_l3.png)
![Rendered by QuickLaTeX.com \[f\left(\sum_{i=1}^{n}t_{i}x_{i}\right)\leqslant\sum_{i=1}^{n}t_{i}\thinspace f\left(x_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-038569d4d96102ba9b789df2a6987325_l3.png)
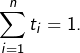
![]()
![Rendered by QuickLaTeX.com \[\frac{1}{n}\,\sum_{k=0}^{n-1}\,f\left(\frac{k}{n}\right)=\int_{0}^{1}\,f\left(t\right)\,dt-\frac{1}{2n}\,\left(f\left(1\right)-f\left(0\right)\right)+o\left(\frac{1}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ff9f4b14fc66e5c2a9b47e4bc1205278_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\dfrac{1}{n}\sum_{k=1}^{n-1}f\left(\dfrac{k}{n}\right)\thinspace g\left(\dfrac{k+1}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-68f0d8dcaa8a50debbab05e0ee39ad65_l3.png)
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{1}{n}\sum_{k=1}^{n}f\left(\dfrac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0ba3585cb6997761631e52d050054af9_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\sum_{k=0}^{n-1}\left|\int_{x_{k,n}}^{x_{k+1,n}}f\left(t\right)\thinspace dt\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d133ea7bcdb627210111c8d66883b313_l3.png)
![]()
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{1}{n}\thinspace\sum_{k=1}^{n}f\left(\dfrac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9c2d5b8fbd0fbb04d5ea0e31e7fd0213_l3.png)