Indications - Exercices sur le second degré - 02

Indications pour démarrer les exercices sur le second degré (fiche 02).
Cliquer ici pour accéder aux énoncés.

Il suffit d’appliquer la règle qui donne le signe d’un trinôme. Profitons-en pour rappeler (voir la fiche n° 1 sur le second degré) que dans le cas d’un trinôme de l’une des deux formes $ax^{2}+bx$ ou bien $ax^{2}+c,$ il n’est pas raisonnable de calculer un discriminant !

Réviser la règle qui autorise à multiplier chaque membre d’un inégalité par un même nombre…

Après avoir isolé tous les termes dans un même membre puis effectué une réduction au même dénominateur, on n’a plus qu’à résoudre des inéquations du second degré !

Il suffit d’évaluer $T\left(A\right)$ et de regarder son signe. Idem pour $B$ et $C$ .

Attention : il faut que $m\neq0$ pour qu’il s’agisse d’une véritable équation du second degré. Une fois cette condition remplie, penser au discriminant…

Le discriminant doit déjà être strictement positif. Exprimer ensuite la somme des racines à l’aide des coefficients du trinôme…

Il suffit d’exprimer $\alpha^{2}+\beta^{2}$ à l’aide de $\alpha+\beta$ et $\alpha\beta$ (expressions dont les valeurs sont connues). Idem pour les deux autres.

Calculer les coordonnées $x,y$ du sommet $S$ puis trouver une équation cartésienne de la courbe décrite par $S$ : pour cela il faudra éliminer $b$ entre $x$ et $y.$

En guise d’indication, voici une version détaillée de l’énoncé :
Soient $a,b,c$ des entiers impairs tels que l’équation $\left(E\right)\quad ax^{2}+bx+c=0$ possède deux solutions réelles. On se propose de montrer que celles-ci sont irrationnelles.

Montrer que si 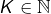$K\in\mathbb{N}$ n’est pas un carré parfait, alors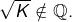 $\sqrt{K}\notin\mathbb{Q}.$
Que dit la contraposée de l’implication précédente ?
Soit 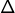$\Delta$ le discriminant de 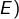$\left E\right)$ (c’est un entier naturel). Montrer que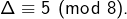 $\Delta\equiv5\pmod{8}.$
Montrer que si l’une des solutions de 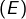$\left(E\right)$ est rationnelle, alors 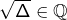$\sqrt{\Delta}\in\mathbb{Q}$ et conclure.

Partager cet article