Neuf énoncés d’exercices sur la notion de nombre premier (fiche 01).

Factoriser l’expression ![]()
Prouver alors que l’entier ![]() est composé.
est composé.

Montrer que pour tout nombre premier ![]() l’entier
l’entier ![]() est multiple de
est multiple de ![]()

Quels sont les palindromes premiers possédant un nombre pair de chiffres décimaux ?

Deux entiers naturels supérieurs ou égaux à 2 sont dits « amicaux » si chacun d’eux est égal à la somme des diviseurs stricts de l’autre. C’est par exemple le cas de 220 et 284; en effet, les diviseurs stricts de 220 sont :
![]()
![]()
![]()
![]()
Montrer que si
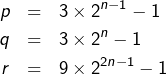
![]()

Soient ![]() tels que
tels que ![]()
Calculer ![]()

Montrer que si ![]() est premier, alors
est premier, alors ![]() est premier.
est premier.

Déterminer les couples ![]() pour lesquels
pour lesquels ![]() est un nombre premier.
est un nombre premier.

Démontrer que si ![]() est premier et si
est premier et si ![]() alors
alors ![]() est multiple de
est multiple de ![]()
En déduire le « petit théorème de Fermat » :
Si ![]() est premier, alors
est premier, alors ![]() est multiple de
est multiple de ![]() pour tout
pour tout ![]()

Pour tout ![]() , on note
, on note ![]() . L’entier
. L’entier ![]() est appelé le
est appelé le ![]() ème nombre de Fermat.
ème nombre de Fermat.
Simplifier, pour tout ![]() , l’expression
, l’expression 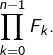 En déduire que les nombres de Fermat sont deux à deux premiers entre eux.
En déduire que les nombres de Fermat sont deux à deux premiers entre eux.
Cliquer ici pour accéder aux indications.
Cliquer ici pour accéder aux solutions.

