Solutions détaillées de neuf exercices sur la notion de nombre premier (fiche 01).
Cliquer ici pour accéder aux énoncés.


On observe que, pour tout couple ![]() d’entiers naturels :
d’entiers naturels :
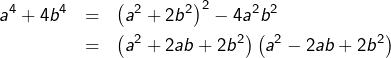
En particulier, pour
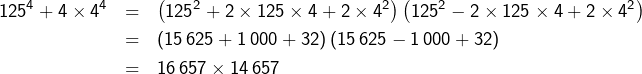
Bref :
![]()

Comme ![]() est impair, alors
est impair, alors ![]() et
et ![]() sont deux nombres pairs consécutifs, ce qui impose à l’un d’eux (seulement) d’être multiple de
sont deux nombres pairs consécutifs, ce qui impose à l’un d’eux (seulement) d’être multiple de ![]() Donc
Donc ![]() est multiple de
est multiple de ![]()
Comme ![]() et vu que 3 et 8 sont premiers entre eux, il reste à prouver que
et vu que 3 et 8 sont premiers entre eux, il reste à prouver que ![]() est multiple de 3.
est multiple de 3.
Mais comme ![]() alors en particulier
alors en particulier ![]() et donc de deux choses l’une :
et donc de deux choses l’une :
- soit
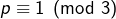
- soit
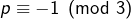
Dans les deux cas : ![]() ce qui permet de conclure.
ce qui permet de conclure.

Notons ![]() la somme des diviseurs positifs de
la somme des diviseurs positifs de ![]() pour tout entier
pour tout entier ![]() .
.
La condition « ![]() et
et ![]() sont amicaux » équivaut à
sont amicaux » équivaut à ![]() On constate que :
On constate que :
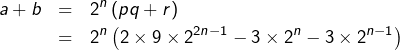
c’est-à-dire :
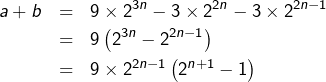
Comme ![]() et
et ![]() sont premiers et distincts, alors les diviseurs de
sont premiers et distincts, alors les diviseurs de ![]() sont :
sont :
- les
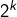 pour
pour 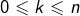
- les
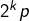 pour
pour 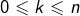
- les
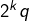 pour
pour 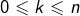
- les
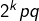 pour
pour 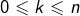
Leur somme est donc :
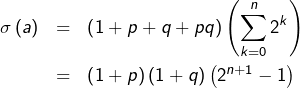
Quant aux diviseurs de ![]() et vu que
et vu que ![]() est premier, ce sont :
est premier, ce sont :
- les
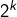 pour
pour 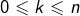
- les
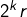 pour
pour 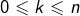
d’où leur somme :
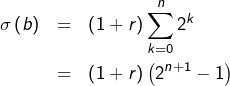
Mais il est clair que
Donc :
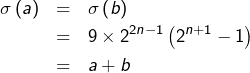
comme souhaité.

L’une des clefs de cet exercice est l’identité remarquable :
(1) ![]()
(2) ![]()
![]()
![]()
Or, les trois nombres ![]()
![]() et
et ![]() sont des entiers supérieurs ou égaux à
sont des entiers supérieurs ou égaux à ![]() donc décomposables en produits de facteurs premiers.
donc décomposables en produits de facteurs premiers.
Si l’un (au moins) d’entre-eux était composé, le produit des trois possèderait au moins quatre facteurs premiers, ce qui est en désaccord avec le membre de droite, produit de seulement trois facteurs.
On voit ainsi que ![]()
![]() et
et ![]() sont premiers. Par unicité de la décomposition en facteurs premiers, on a nécessairement :
sont premiers. Par unicité de la décomposition en facteurs premiers, on a nécessairement :
![]()
![]()
![]()

Soit ![]() un tel entier et
un tel entier et ![]() le nombre (supposé pair) de ses chiffres décimaux (avec
le nombre (supposé pair) de ses chiffres décimaux (avec ![]() Il existe alors des entiers
Il existe alors des entiers ![]() tels que :
tels que :
![]()
![Rendered by QuickLaTeX.com \[N=\sum_{i=0}^{r-1}a_{i}\left(10^{i}+10^{2r-1-i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-32fc43a4994a544e82c333977691d580_l3.png)
![Rendered by QuickLaTeX.com \[N=\sum_{i=0}^{r-1}a_{i}10^{i}\left(1+10^{2r-2i-1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3a7f30326b71d06c0c5c064a3e77876a_l3.png)
Il s’ensuit que ![]() est multiple de
est multiple de ![]() et donc que
et donc que ![]() ne peut être premier… sauf bien entendu si
ne peut être premier… sauf bien entendu si ![]() (c’est-à-dire si
(c’est-à-dire si ![]()

On sait que, pour tout couple ![]() d’entiers naturels et pour tout entier
d’entiers naturels et pour tout entier ![]() :
:
![]()
![]()
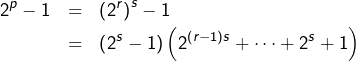
![]()
![]()
![]()

On va chercher d’éventuels nombres premiers dans la « moitié gauche » du triangle de Pascal c’est-à-dire parmi les ![]() avec
avec ![]()
Vue la formule ![]() ceci se fait sans perte de généralité.
ceci se fait sans perte de généralité.
Soient ![]() deux entiers naturels tels que
deux entiers naturels tels que ![]()
D’après la formule du pion (on pourra consulter cette vidéo) :
![]()
![]()
![]()
![]()
![]()
![]()
En conclusion, les seuls couples ![]() pour lesquels
pour lesquels ![]() est premier sont les
est premier sont les ![]() et les
et les ![]() avec
avec ![]() premier.
premier.

Soit ![]() un nombre premier et soit
un nombre premier et soit ![]() un entier tel que
un entier tel que ![]() D’après la formule du pion :
D’après la formule du pion :
![]()
![]()
![]()
Ensuite, on prouve par récurrence que, pour tout ![]() :
:
![]()
➢ C’est vrai pour ![]() de manière évidente.
de manière évidente.
➢ Supposons cette congruence vraie pour un certain ![]() Alors, d’après la formule du binôme :
Alors, d’après la formule du binôme :
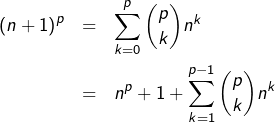
![]()
![]()

On observe que, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\prod_{k=0}^{n-1}\left(2^{2^{k}}+1\right)=\prod_{k=0}^{n-1}\frac{\left(2^{2^{k}}+1\right)\left(2^{2^{k}}-1\right)}{2^{2^{k}}-1}=\prod_{k=0}^{n 1}\frac{2^{2^{k+1}}-1}{2^{2^{k}}-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-035b2502791270fddcca2148d617dea3_l3.png)
![Rendered by QuickLaTeX.com \[\prod_{k=0}^{n-1}F_{k}=2^{2^{n}}-1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f29a044553779ab66d587b4eea6c374d_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\prod_{k=0}^{n-1}F_{k}=F_{n}-2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ab4cf12f08d097a8cde779ab871d75fe_l3.png)
Maintenant, supposons que deux nombres de Fermat, disons ![]() et
et ![]() pour
pour ![]() ne soient pas premiers entre eux et soit
ne soient pas premiers entre eux et soit ![]() un diviseur commun. D’après la relation ci-dessus, on voit que
un diviseur commun. D’après la relation ci-dessus, on voit que ![]() et donc
et donc ![]() Mais ceci est absurde car les nombres de Fermat sont des entiers impairs.
Mais ceci est absurde car les nombres de Fermat sont des entiers impairs.
On a prouvé par l’absurde que les entiers ![]() sont deux à deux premiers entre eux.
sont deux à deux premiers entre eux.
Remarque
Si l’on note ![]() le plus petit facteur premier de
le plus petit facteur premier de ![]() alors l’application
alors l’application ![]() est injective, d’après cette dernière propriété. On retrouve ainsi le fait que l’ensemble des nombres premiers est infini.
est injective, d’après cette dernière propriété. On retrouve ainsi le fait que l’ensemble des nombres premiers est infini.
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
