Il est évident que si 
vérifient les conditions 
et 
alors 
et 
En effet, 
et 
doivent être (non nuls et) de même signe puisque leur produit est strictement positif; et ce signe commun est déterminé par le fait que 
Soient maintenant 
tels que :
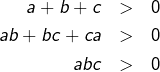
Sauriez-vous montrer que
?
Et sauriez-vous généraliser ceci à un nombre quelconque de termes ?
Une solution est disponible ici
On reconnaît les fonctions symétriques élémentaires des racines d’un polynôme. En utilisant lien entre coefficients et racines, le résultat s’obtient en remarquant que pour un polynôme unitaire P de la forme correspondant à vos contraintes, si x est négatif on n’a jamais P(x) = 0 (c’est strictement positif si le degré de P est pair et strictement négatif dans le cas contraire), donc les racines de P sont toutes strictement positives.