
1 – De quoi s’agit-il ?
En mathématiques, on doit souvent établir des implications.
Il s’agit d’énoncés du type :
Si P est vraie, alors Q est vraie
P et Q désignent deux propositions :
P est l‘hypothèse (ou la prémisse) et Q est la conclusion.
➡ Ce qu’il ne faut absolument pas faire : ré-écrire l’hypothèse et la transformer, au petit bonheur la chance, en espérant parvenir ainsi jusqu’à la conclusion.
➡ Ce qu’il faut faire : viser la cible (c’est-à-dire la conclusion).

Examinons quelques exemples …
2 – Un premier exemple
Etant donnés deux ensembles ![]() et
et ![]() on demande d’établir :
on demande d’établir :
![]()
Cet exemple est rudimentaire, mais suffisant pour qu’on puisse déjà percevoir un principe général.
Ici, la cible est l’inclusion ![]() Il faut donc se donner un élément quelconque de
Il faut donc se donner un élément quelconque de ![]() et prouver qu’il appartient nécessairement à
et prouver qu’il appartient nécessairement à ![]()
En cours de route, on utilisera bien sûr l’hypothèse… mais seulement au moment opportun !
Allons-y :
Preuve (cliquer pour déplier / replier)
Soit ![]() .
.
Comme ![]() alors
alors ![]() c’est-à-dire
c’est-à-dire ![]() et
et ![]()
En particulier : ![]()
Remarquer l’utilisation du mot “ soit ”.
En écrivant “ Soit ![]() ”, on introduit un objet dans le contexte de la démonstration : il s’agit, en l’occurrence, d’un élément quelconque de
”, on introduit un objet dans le contexte de la démonstration : il s’agit, en l’occurrence, d’un élément quelconque de ![]()
Il faut veiller à ce que les divers objets présents dans le contexte aient tous été introduits antérieurement (par nos soins ou bien par l’énoncé lui-même).
Il serait farfelu d’écrire “ Soient ![]() deux ensembles ” dans cette preuve, puisque l’énoncé a déjà introduit ces deux objets !
deux ensembles ” dans cette preuve, puisque l’énoncé a déjà introduit ces deux objets !
Montrons maintenant que :
![]()
C’est l’implication réciproque de la précédente : l’hypothèse et la conclusion ont été purement et simplement échangées.
Comme ci-dessus, on vise la cible, c’est-à-dire l’égalité ![]()
On sait que l’égalité entre deux ensembles consiste, par définition, en deux inclusions réciproques.
On doit donc se donner un quelconque élément de ![]() et prouver qu’il appartient nécessairement à
et prouver qu’il appartient nécessairement à ![]() puis se donner un quelconque élément de
puis se donner un quelconque élément de ![]() et prouver qu’il appartient nécessairement à
et prouver qu’il appartient nécessairement à ![]()
La première de ces deux inclusions est “ banale ” en ce sens qu’elle reste vraie, même sans l’hypothèse ![]() Elle est “vraie en toute généralité ”, ce qui – en revanche – n’est pas le cas de la seconde implication. Voici ce qu’il faut faire :
Elle est “vraie en toute généralité ”, ce qui – en revanche – n’est pas le cas de la seconde implication. Voici ce qu’il faut faire :
Preuve (cliquer pour déplier / replier)
Soit ![]() Par hypothèse :
Par hypothèse : ![]() donc
donc ![]() Ainsi
Ainsi ![]() et
et ![]() Autrement dit :
Autrement dit : ![]()
On a montré que (sous l’hypothèse ![]() ) :
) : ![]()
Quant à l’inclusion ![]() elle est vraie en toute généralité.
elle est vraie en toute généralité.
Au final, on a prouvé que chacune des assertions ![]() et
et ![]() implique l’autre. On exprime cela en disant que ces deux assertions sont équivalentes, ce qu’on note :
implique l’autre. On exprime cela en disant que ces deux assertions sont équivalentes, ce qu’on note :
![]()
3 – Une autre implication
Considérons ![]() et
et ![]() deux applications de
deux applications de ![]() dans lui-même et prouvons que :
dans lui-même et prouvons que :
![]()
Avant tout, on identifie la cible ! Il s’agit de montrer, en notant ![]() , que :
, que :
![]()
On commence donc mécaniquement la preuve comme ceci :
Soient ![]() et
et ![]() …
…
et l’on s’efforce, après quelques étapes, d’aboutir à :
… et donc ![]()
Allons-y …
Preuve (cliquer pour déplier / replier)
Soient ![]() et
et ![]() Comme
Comme ![]() est convexe, alors :
est convexe, alors :
![]()
![]()
![]()
Ainsi :
![]()
et la convexité de ![]() est établie.
est établie.
4 – Une implication en cache parfois une autre !
Il peut arriver qu’en démontrant une implication ![]() , on se rende compte que cette preuve « contient », en quelque sorte, la preuve de l’implication réciproque. Donnons deux exemples :
, on se rende compte que cette preuve « contient », en quelque sorte, la preuve de l’implication réciproque. Donnons deux exemples :
Exemple 1
Considérons une bijection ![]() et montrons que :
et montrons que :
![]()
Bien entendu, ![]() désigne la bijection réciproque de
désigne la bijection réciproque de ![]() .
.
Quelle est la cible ? Il faut prouver que :
![]()
Soit ![]() On a d’une part (par définition de
On a d’une part (par définition de ![]() ) :
) :
![]()
![]()
![]()
Comme ![]() est injective, il s’ensuit que :
est injective, il s’ensuit que :
![]()
Il faut noter qu’en montrant cette implication, on a aussi montré sa réciproque !
Il suffit en effet d’appliquer le résultat à ![]()
Exemple 2
Soit ![]() on pose pour tout
on pose pour tout ![]() :
:
![]()
En fait, là encore, il suffira de montrer que :
![]()
En effet, si ![]() est convexe alors l’application
est convexe alors l’application ![]() sera convexe, mais pour tout
sera convexe, mais pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[x\thinspace g\left(\frac{1}{x}\right)=x\thinspace\frac{1}{x}\thinspace f\left(\frac{1}{\left(\frac{1}{x}\right)}\right)=f\left(x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-00c112d0985e81ec6fcfb3e1039abc84_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\mu=\frac{1}{\frac{1}{x}-\frac{1}{y}}\left(\frac{1}{\left(1-t\right)x+ty}-\frac{1}{y}\right)=\frac{\left(1-t\right)x}{\left(1-t\right)x+ty}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-33c2ba2f39f94253db3183faee7e0bec_l3.png)
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}g\left(\left(1-t\right)x+ty\right) & = & \left(\left(1-t\right)x+ty\right)\,f\left(\frac{\mu}{x}+\frac{1-\mu}{y}\right)\\& \leqslant & \left(\left(1-t\right)x+ty\right)\,\left[\mu\,f\left(\frac{1}{x}\right)+\left(1-\mu\right)\,f\left(\frac{1}{y}\right)\right]\\& = & \left(1-t\right)x\,f\left(\frac{1}{x}\right)+ty\,f\left(\frac{1}{y}\right)\\& = & \left(1-t\right)\,g\left(x\right)+t\,g\left(y\right)\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-a615d7bfb661ef05e816f1ce78904440_l3.png)
5 – Un dernier exemple, plus élaboré
Soit ![]() un ensemble et soit
un ensemble et soit ![]() une application.
une application.
On dit que ![]() est “ simplifiable à gauche ” lorsque :
est “ simplifiable à gauche ” lorsque :
![]()
On se propose de montrer que :
![]()
Occupons-nous, pour commencer, de l’implication ![]() :
:
La cible est “ ![]() est injective ”. Il faut donc mécaniquement commencer par “ soient
est injective ”. Il faut donc mécaniquement commencer par “ soient ![]() tels que
tels que ![]() » et aboutir un peu plus bas à “ … et donc
» et aboutir un peu plus bas à “ … et donc ![]() « .
« .
Mais une fois qu’on a écrit les premiers mots, la suite de la preuve n’est pas évidente à trouver … D’ailleurs, si c’était toujours aussi évident qu’à la première section, ça voudrait dire que les maths, c’est facile (et vous savez qu’il n’en est rien).
Comment faire ? Il faut naturellement faire intervenir l’hypothèse et donc fabriquer deux applications ![]() et
et ![]() sur mesure. Voici comment :
sur mesure. Voici comment :
Preuve (cliquer pour déplier / replier)
Soient ![]() tels que
tels que ![]()
Raisonnons par l’absurde et supposons ![]()
On peut alors construire une application ![]() en posant :
en posant :
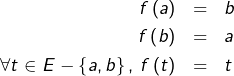
On constate que ![]() bien que
bien que ![]()
Ceci est en contradiction avec l’hypothèse et donc ![]()
Passons à l’implication réciproque ![]()
Cette fois, la cible est :
![]()
La situation s’est compliquée car la cible est elle-même une implication !
Mais on sait maintenant par quoi il faut commencer …
Preuve (cliquer pour déplier / replier)
Soient ![]() telles que
telles que ![]()
Pour tout ![]() :
:
![]()
Ainsi ![]()
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
