Question
Quelles sont les conditions pour que deux applications commutent ?
Réponse
Considérons quatre ensembles ![]() et deux applications
et deux applications
![]()
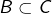 pour pouvoir envisager
pour pouvoir envisager 
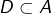 pour pouvoir envisager
pour pouvoir envisager 
Ces deux inclusions étant supposées vraies, on dispose des applications composées :
![]()
La condition ![]() se traduit alors par les trois conditions supplémentaires suivantes :
se traduit alors par les trois conditions supplémentaires suivantes :
- l’égalité des ensembles de départ :
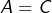
- l’égalité des ensembles d’arrivée :
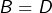
- pour tout
 :
: 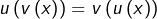
Bref, les conditions requises sont :
![]()
![]()
Exemple
![]()
définies par :
![Rendered by QuickLaTeX.com \[\left.\begin{array}{ccc}u\left(1\right) & = & 1\\u\left(2\right) & = & 2\\u\left(3\right) & = & 1\end{array}\right\}\qquad\text{et}\qquad\left\{\begin{array}{ccc}v\left(1\right) & = & 2\\v\left(2\right) & = & 1\\v\left(3\right) & = & 2\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d6eccf3445405e8cfdfe751f059358b7_l3.png)
On vérifie aisément que ![]()

