(n+1)(n+2)...(n+k) est multiple de k!

1 – Introduction

Le problème suivant a été soumis aux élèves d’une classe de troisième :

Prouver que la somme de cinq entiers consécutifs est multiple de 5.

Ce n’est pas bien difficile : en notant ces cinq entiers $n-2,$ $n-1,$ $n,$ $n+1$ et $n+2,$ leur somme est égale à $5n,$ ce qui règle la question.

On peut d’ailleurs généraliser en remplaçant 5 par n’importe quel entier naturel impair :

Proposition 1

Pour tout $p\in\mathbb{N},$ la somme de $2p+1$ entiers consécutifs est multiple de $2p+1.$

En effet, si l’on note $k+i$ ces entiers, avec $-p\leqslant i\leqslant p$ et $k\in\mathbb{Z},$ on constate que :

$\sum_{i=-p}^{p}\left(k+i\right)=\left(2p+1\right)k$

Notons que ça ne marche pas avec un nombre pair de termes !

Par exemple : 1 + 2 + 3 + 4 = 10 n’est pas multiple de 4.

Maintenant, si l’on remplace somme par produit, les choses vont devenir plus intéressantes.

Quel pourrait être l’énoncé analogue pour un produit d’entiers consécutifs ? Observons un peu avant de nous lancer…

Le produit de deux entiers consécutifs est pair, car l’un des deux facteurs l’est !
Le produit de trois entiers consécutifs est multiple de 3, puisque l’un des trois facteurs l’est.

Il est clair que ceci se généralise, pour donner :

Proposition 2

Pour tout entier k, supérieur ou égal à 1, le produit de k entiers consécutifs est multiple de k.

On trouve en effet, parmi $k$ entiers consécutifs, un multiple de $k$ (et un seul, d’ailleurs).

Mais on peut obtenir bien mieux ! Nous allons démontrer de plusieurs façons le :

Théorème (T)

Pour tout entier k supérieur ou égal à 1,le produit de k entiers consécutifs est multiple de k!

➣ Pour k = 1, l’affirmation est triviale.

➣ Pour k = 2, on affirme que le produit de deux entiers consécutifs est pair, ce qui est connu.

➣ Pour k = 3, il y a du nouveau : le théorème stipule que le produit de trois entiers consécutifs est multiple de 3! = 6, ce qui s’explique aisément. Un tel produit est en effet multiple de 2 et de 3, donc de 6 puisque 2 et 3 sont premiers entre eux.

Etant donnés des entiers $a,b$ et $c$ tels que $c$ soit multiple de $a$ et de $b,$ il ne faut pas conclure hâtivement que $c$ est multiple du produit $ab,$ car c’est en général faux ! Par exemple :

12 est multiple de 4 et de 6, mais 12 n’est pas multiple de 24.

Cependant :

Proposition 3

Si a et b sont premiers entre eux et si c est multiple de a et de b, alors c est multiple de ab.

Preuve (cliquer pour déplier / replier)

Comme $a$ et $b$ sont premiers entre eux, il existe des entiers $p$ et $q$ tels que $pa+qb=1$ (identité de Bézout). Il s’ensuit que $c=pac+qbc.$

Or, il existe par hypothèse des entiers $k,\ell$ tels que $c=ka=b\ell.$

Ainsi : $c=pab\ell+qbka=ab\left(p\ell+qk\right).$ On a bien montré que $c$ est multiple de $ab.$

➣ Voici un autre point de vue …

Comme $c$ est multiple de $a$ et de $b,$ alors $c$ est multiple de $m=PPCM\left(a,b\right).$ Or, (propriété générale) en notant $d=PGCD\left(a,b\right),$ on a : $md=ab.$ Vu que $d=1,$ cette dernière égalité devient $m=ab,$ ce qui donne la conclusion.

Examinons encore un cas particulier du théorème (T), celui où k = 4.

Il s’agit de comprendre pourquoi le produit de quatre entiers consécutifs est multiple de 24.

Comme 24 = 3 $\times$ 8 et vu que 3 et 8 sont premiers entre eux, il suffit (d’après la proposition 3 ci-dessus) de vérifier que ce produit est multiple de 3 et de 8.

➣ Le fait qu’il soit multiple de 3 a déjà été expliqué.

➣ Par ailleurs, ce produit comporte deux facteurs pairs qui sont respectivement de la forme $4q$ et et $4q\pm2,$ il est donc clairement multiple de 8.

L’examen du cas k = 5 est laissé en exercice, pour le lecteur intéressé 😉

Il est temps d’aborder la preuve du théorème (T) dans le cas général.

Nous pouvons nous limiter à des entiers naturels consécutifs. Il ne s’agit pas là d’une restriction, puisque si l’un de ces $k$ entiers consécutifs est nul, alors leur produit aussi (et 0 est bien multiple de $k!)$ et s’ils sont tous négatifs, alors leur produit vaut $\left(-1\right)^{k}A,$ où $A$ est le produit de $k$ entiers consécutifs positifs.

Trois preuves du théorème (T) sont proposées dans les sections suivantes.

2 – Une preuve combinatoire

Si l’on connaît les coefficients binomiaux, on ne peut pas s’empêcher d’observer qu’en notant $N=\left(n+1\right)\left(n+2\right)\cdots\left(n+k\right)$ et $D=1\times 2\times \cdots\times k = k!$ , on obtient :

$\frac{N}{D}=\frac{\left(n+k\right)!}{k!\thinspace n!}=\binom{n+k}{k}$

qui est un entier naturel. Fin de l’histoire.

Pour que l’explication soit complète, il faut bien sûr rappeler que si deux entiers naturels p et k vérifient $k\leqslant p,$ alors $\binom{p}{k}$ désigne par définition le nombre de parties de cardinal k d’un ensemble de cardinal p (et c’est donc évidemment un entier naturel). Mais ce n’est pas tout, car il faut aussi établir la formule (dite de Fermat) selon laquelle :

$\binom{p}{k}=\frac{p!}{k!\thinspace\left(p-k\right)!}$

Tout ceci est expliqué en détail dans cet article sur les coefficients binomiaux, auquel vous pourrez vous reporter si nécessaire.

3 – Une preuve arithmétique

Dans ce qui suit, nous utiliserons le théorème fondamental de l’arithmétique, selon lequel tout entier $n$ supérieur ou égal à $2$ se décompose en produit de nombres premiers, sous la forme :

$n=p_{1}^{\alpha_{1}}\cdots p_{r}^{\alpha_{r}}$

avec $p_{1},\cdots,p_{r}$ premiers distincts et $\alpha_{1},\cdots,\alpha_{r}$ entiers naturels non nuls.

En outre, cette décomposition en facteurs premiers (ou DFP) est unique (à l’ordre près des facteurs).

Si $p$ est un diviseur premier de $n,$ l’exposant de $p$ dans la DFP de $n$ est appelé « valuation $p-$ adique de $n$ » et noté $v_{p}\left(n\right).$

Et si le nombre premier $p$ n’est pas un diviseur de $n,$ on convient que $v_{p}\left(n\right)=0.$

Avec cette définition, il est facile de prouver que :

$\fcolorbox{black}{myBlue}{$v_{p}\left(mn\right)=v_{p}\left(m\right)+v_{p}\left(n\right)$}$

pour tout couple $\left(m,n\right)$ d’entiers naturels non nuls et pour tout nombre premier $p$ .

Voici maintenant le principe sur lequel repose notre preuve arithmétique du théorème (T) :

Principe :

Etant donnés des entiers naturels non nuls $N$ et $D,$ il suffit pour montrer qu’une fraction $\frac{N}{D}$ représente un nombre entier, de prouver que pour tout $p$ premier :

$v_{p}\left(D\right)\leqslant v_{p}\left(N\right)$

Dans le cas qui nous intéresse :

$\frac{N}{D}=\frac{\left(n+1\right)\cdots\left(n+k\right)}{k!}=\frac{\left(n+k\right)!}{k!\thinspace n!}$

Il suffit donc de prouver que, pour tout $p$ premier :

$v_{p}\left(k!\right)+v_{p}\left(n!\right)\leqslant v_{p}\left(\left(n+k\right)!\right)\qquad\left(\star\right)$

C’est là qu’intervient la formule de Legendre, qui donne la valuation $p-$ adique d’une factorielle :

Théorème (Formule de Legendre)

Si $n\in\mathbb{N}^{\star}$ et $p\in\mathbb{P},$ alors :

$v_{p}\left(n!\right)=\sum_{j=1}^{\infty}\left\lfloor \frac{n}{p^{j}}\right\rfloor$

La partie entière de $\frac{n}{p^{j}}$ étant nulle dès que $p$ est assez grand, la somme ci-dessus est finie (contrairement aux apparences).

Pour ceux que ça intéresse, une preuve de cette célèbre formule est donnée en annexe.

Avec cette relation en poche, on voit que :

$v_{p}\left(\left(n+k\right)!\right)-v_{p}\left(k!\right)-v_{p}\left(n!\right)=\sum_{p=1}^{\infty}\left(\left\lfloor \frac{n+k}{p^{j}}\right\rfloor -\left\lfloor \frac{n}{p^{j}}\right\rfloor -\left\lfloor \frac{k}{p^{j}}\right\rfloor \right)$

Or, pour tout couple $\left(x,y\right)$ de nombres réels, on a :

$\left\lfloor x\right\rfloor \leqslant x\qquad\text{et}\qquad\left\lfloor y\right\rfloor \leqslant y$

d’où :

$\left\lfloor x\right\rfloor +\left\lfloor y\right\rfloor \leqslant x+y$

et donc, par définition de la partie entière de $x+y$ :

$\left\lfloor x\right\rfloor +\left\lfloor y\right\rfloor \leqslant\left\lfloor x+y\right\rfloor$

L’inégalité $\left(\star\right)$ en résulte.

4 – Une preuve par double récurrence

Le lecteur peu familier avec la méthode de démonstration par récurrence pourra consulter l’article Qu’est-ce qu’une preuve par récurrence ?

Prouvons que l’assertion :

$\mathcal{A}_{k}$ : « le produit de $k$ entiers naturels consécutifs est multiple de $k!$ «

est vraie pour tout $k\geqslant1.$

➣ D’évidence, $\mathcal{A}_{1}$ est vraie.

➣ Supposons $\mathcal{A}_{k}$ vraie pour un certain $k\geqslant1$ et montrons que $\mathcal{A}_{k+1}$ est vraie. Pour cela, montrons par récurrence sur $n$ que l’assertion $\mathcal{B}_{k,n}$ suivante :

$\left(n+1\right)\cdots\left(n+k+1\right)$ est multiple de $\left(k+1\right)!$

est vraie pour tout $n\in\mathbb{N}.$

➢ D’évidence, $\mathcal{B}_{k,0}$ est vraie.

➢ Supposons $\mathcal{B}_{k,n}$ vraie pour un certain $n\in\mathbb{N}.$ Autrement dit :

$\left(n+1\right)\cdots\left(n+k+1\right)=\lambda\left(k+1\right)!\qquad\text{avec }\lambda\in\mathbb{N}$

On constate, en posant $A=\left(n+2\right)\cdots\left(n+k+1\right),$ que :

$\begin{equation*}\begin{split}\left(n+2\right)\cdots\left(n+k+2\right) & = \left(n+2\right)\cdots\left(n+k+1\right)\left[\left(n+1\right)+\left(k+1\right)\right]\\& = \left(n+1\right)\cdots\left(n+k+1\right)+\left(k+1\right)A\\& = \lambda\left(k+1\right)!+\left(k+1\right)A\end{split}\end{equation*}$

Comme $A$ est le produit de $k$ entiers consécutifs, c’est un multiple de $k!$ d’après $\mathcal{A}_{k}.$ Ainsi $\left(n+2\right)\cdots\left(n+k+2\right)$ est multiple de $\left(k+1\right)!$ autrement dit $\mathcal{B}_{k,n+1}$ est vraie.

On a montré que $\mathcal{A}_{k+1}$ est vraie et le tour est donc joué. Au passage, c’est un joli exemple de deux récurrences emboîtées.

5 – Que dire de plus ?

Nous avons établi de trois façons que, pour tout entier $k\geqslant1,$ le produit de $k$ entiers consécutifs est nécessairement multiple de la factorielle de $k.$ Ce résultat constitue une amélioration substantielle de la proposition 2 énoncée dans l’introduction. Peut-il être encore amélioré ?

Voici deux pistes de réflexion :

Piste 1

Trouver, si possible, un diviseur non trivial de $\left(n+1\right)\cdots\left(n+k\right)$ qui soit plus « gros » que la factorielle de $k.$ Cette question ne semble pas facile.

Piste 2

Trouver en fonction de $k$ et $q$ une estimation de $n_{k,q}$ = le plus petit $n$ pour lequel $\left(n+1\right)\cdots\left(n+k\right)$ est divisible par $q!$ (avec $q>k$ donné).

Je m’explique : pour $1\leqslant q\leqslant k,$ la question n’a aucun intérêt puisque tout entier $n\geqslant1$ convient (c’est ce que dit notre théorème (T)).

Pour $q=k+1,$ il est clair que $n=1$ convient.

Dès que $q>k+1,$ les choses cessent d’être simples, mais un tel $n$ existe (puisque $n=q!-1$ convient), ce qui rend licite la définition de $n_{k,q}$ .

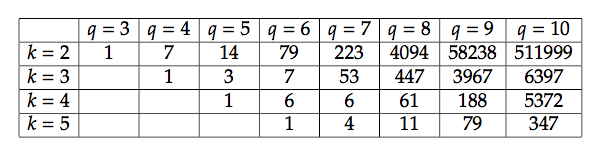
Le tableau ci-dessus donne les valeurs de $n_{k,q}$ pour quelques couples $\left(k,q\right)$ : Par exemple, le fait que $n_{5,10}=347$ signifie que :

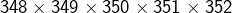$348\times349\times350\times351\times352$ est divisible par $10!=3628800$ ,
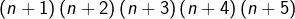$\left(n+1\right)\left(n+2\right)\left(n+3\right)\left(n+4\right)\left(n+5\right)$ n’est divisible par 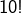$10!$ pour aucun $n\in\llbracket0,346\rrbracket.$

Citons pour finir un résultat difficile, publié en 1974 par Paul Erdös et John Selfridge (consultable ici) :

Le produit d’au moins deux entiers naturels non nuls consécutifs n’est jamais une puissance parfaite (c’est-à-dire : n’est jamais de la forme $N^{r}$ avec $r\geqslant2$ et $N\in\mathbb{N}).$

Annexe

Théorème (Formule de Legendre)

Si $n\in\mathbb{N}^{\star}$ et $p\in\mathbb{P},$ alors :

$v_{p}\left(n!\right)=\sum_{j=1}^{\infty}\left\lfloor \frac{n}{p^{j}}\right\rfloor$

Commençons par un mini-exercice de dénombrement.

Exercice

Etant donnés deux entiers naturels non nuls n et q, combien existe-t-il d’entiers compris (au sens large) entre 1 et n qui sont multiples de q ?

Solution (cliquer pour déplier / replier)

Ces entiers sont les $\lambda q,$ avec $1\leqslant\lambda\leqslant\frac{n}{q};$ la réponse est donc immédiate : il en existe $\left\lfloor \frac{n}{q}\right\rfloor .$

Par exemple, les multiples de 23 compris entre 1 et 7654 sont au nombre de $\left\lfloor \frac{7654}{23}\right\rfloor =332.$

A présent, abordons la preuve de la formule de Legendre.

Les entiers compris entre 1 et $n$ peuvent être classés selon leur valuation $p-$ adique.

Ceux dont la valuation $p-$ adique est $j$ (pour $j\in\mathbb{N}$ donné) sont les multiples de $p^{j}$ qui ne sont pas multiples de $p^{j+1}.$ Ils sont donc au nombre de $\left\lfloor \frac{n}{p^{j}}\right\rfloor -\left\lfloor \frac{n}{p^{j+1}}\right\rfloor .$

En notant $E_{j}$ leur ensemble, on observe que :

$\llbracket1,n\rrbracket =\bigsqcup_{j\geqslant0}E_{j}$

Bien entendu $E_{j}=\emptyset$ pour j assez grand et cette union disjointe est donc finie !

Plus précisément, $E_{j}$ est vide dès que $j>n.$ En effet, si $1\leqslant a\leqslant n$ et $v_{p}\left(a\right)>n,$ alors :

$a\geqslant p^{v_{p}\left(a\right)}>p^{n}\geqslant2^{n}>n$

ce qui est absurde !

On utilise ensuite le fait que la valuation $p-$ adique d’un produit est la somme des valuations $p-$ adiques des différents facteurs :

$v_{p}\left(n!\right)=\sum_{k=1}^{n}v_{p}\left(k\right)=\sum_{j\geqslant0}\sum_{k\in E_{j}}v_{p}\left(k\right)=\sum_{j\geqslant0}j\left(\left\lfloor \frac{n}{p^{j}}\right\rfloor -\left\lfloor \frac{n}{p^{j+1}}\right\rfloor \right)$

Le premier terme de la somme est nul. Quant aux suivants, ils se télescopent :

$\begin{equation*}\begin{split}v_{p}\left(n!\right) & = \sum_{j\geqslant1}j\left(\left\lfloor \frac{n}{p^{j}}\right\rfloor -\left\lfloor \frac{n}{p^{j+1}}\right\rfloor \right)\\& = \sum_{j\geqslant1}\left\lfloor \frac{n}{p^{j}}\right\rfloor +\sum_{j\geqslant1}\left(\left(j-1\right)\left\lfloor \frac{n}{p^{j}}\right\rfloor -j\left\lfloor \frac{n}{p^{j+1}}\right\rfloor \right)\\& = \sum_{j\geqslant1}\left\lfloor \frac{n}{p^{j}}\right\rfloor\end{split}\end{equation*}$

ce qui achève la preuve.

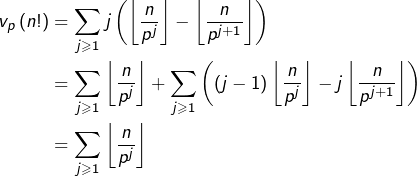
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Partager cet article

Cet article a 5 commentaires

CLAVIER 11 Fév 2023 Répondre

Est-il possible que le produit N=(n+1)…(n+k) soit un carré parfait, un cube parfait ou une puissance d’exposant plus élevée d’un entier ?
1. René Adad 12 Fév 2023 Répondre
  
  Cette question est délicate. Je l’ai signalée quelques lignes avant l’annexe. Vous y trouverez un lien vers un article de Erdös et Selfridge (1974) qui y répond par la négative.
  1. CLAVIER 17 Fév 2023 Répondre
    
    Merci. Désolé, j’avais sauté cette partie de votre article !
    Je n’avais pas vu votre réponse. Les autres fois, je crois que j’avais reçu un mail pour m’en avertir, mais là il me semble bien ne rien avoir reçu.
Joseph Cesana 20 Juil 2018 Répondre

C’est un reel plaisir de lire et d’etudier vos articles… retour aux maths apres tant d’anne’es avec beaucoup d’enthousiasme.

– Joseph Cesana
1. René Adad 21 Juil 2018 Répondre
  
  Merci beaucoup Joseph !