
1 – Qu’est-ce qu’une implication ?
La pratique des mathématiques nous conduit en permanence à rencontrer des énoncés du type :
« SI … ALORS … »
Par exemple, étant donnés deux nombres réels ![]() et
et ![]() positifs ou nuls :
positifs ou nuls :
Si ![]() alors
alors ![]()
A priori, l’hypothèse ![]() peut être vraie ou fausse : cela dépend bien sûr des valeurs attribuées à
peut être vraie ou fausse : cela dépend bien sûr des valeurs attribuées à ![]() et
et ![]() Même chose pour la conclusion
Même chose pour la conclusion ![]()
Ce qui nous intéresse ici, c’est le fait que chaque fois que l’hypothèse est vraie, il en va de même pour la conclusion.
On exprime cela en disant que, quelles que soient les valeurs (positives ou nulles) de ![]() et de
et de ![]() l’hypothèse
l’hypothèse ![]() implique la conclusion
implique la conclusion ![]()
Tout ceci se note, en symboles :
![]()
Pour tout couple ![]() de réels positifs ou nuls, si le carré de
de réels positifs ou nuls, si le carré de ![]() est inférieur ou égal à celui de
est inférieur ou égal à celui de ![]() alors
alors ![]() est inférieur ou égal à
est inférieur ou égal à ![]() .
.
Le symbole ![]() (appelé quantificateur universel) se lit « pour tout … » ou bien « quel que soit … ».
(appelé quantificateur universel) se lit « pour tout … » ou bien « quel que soit … ».
![]()
Ce qui précède suggère l’existence d’un lien de causalité : ![]() serait conséquence de
serait conséquence de ![]()
En fait, il ne s’agit pas de cela. Pour essayer d’y comprendre quelque chose, nous allons employer une petite astuce : passer par la double-négation.
Si quelqu’un prétend qu’une certaine hypothèse ![]() entraîne une certaine conclusion
entraîne une certaine conclusion ![]() et si nous pensons le contraire, nous pourrons exprimer notre désaccord en disant que l’hypothèse
et si nous pensons le contraire, nous pourrons exprimer notre désaccord en disant que l’hypothèse ![]() est vraie mais que la conclusion
est vraie mais que la conclusion ![]() est fausse.
est fausse.
Par exemple, je ne suis pas d’accord pour reconnaître que « si le vent souflle à plus de 80 km/h, alors tous les arbres de la forêt seront penchés ». J’exprime ceci en disant : « le vent souffle à plus de 80 km/h, et pourtant l’un au moins des arbres de la forêt n’est pas penché ».
On conçoit ainsi que la négation de ![]() doit être
doit être ![]()
Par ailleurs, tout le monde s’accordera pour dire que la négation de la négation d’une phrase ![]() possède la même valeur de vérité que
possède la même valeur de vérité que ![]() On découvre ainsi que
On découvre ainsi que ![]() doit être logiquement équivalente à
doit être logiquement équivalente à ![]() autrement dit à
autrement dit à ![]()
Résumons : les écritures
![]()
![]()
Ainsi, la notion de causalité a complètement disparu !
2 – Un truc faux implique n’importe quoi !
Une retombée un peu surprenante de ce qui précède apparaît lorsqu’on construit la table de vérité de l’implication. Il s’agit simplement d’un tableau indiquant la valeur de vérité de ![]() (c’est-à-dire de
(c’est-à-dire de ![]() ) en fonction de celles de
) en fonction de celles de ![]() et de
et de ![]() :
:
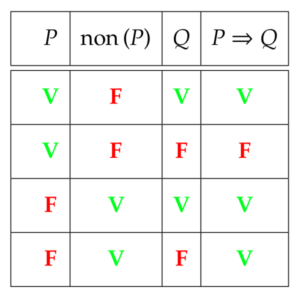
On s’aperçoit notamment que, dans le cas où ![]() est fausse, l’implication
est fausse, l’implication ![]() est vraie… quelle que soit la valeur de vérité de
est vraie… quelle que soit la valeur de vérité de ![]()
![]()
3 – Equivalence logique
![]()
![]()
Afin de résoudre une équation ![]() , on construit une succession d’équations de telle sorte que :
, on construit une succession d’équations de telle sorte que :
- la première d’entre-elles soit l’équation
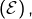
- toutes ces équations possèdent le même ensemble de solutions,
- la dernière équation admette un ensemble de solutions facile à déterminer.
Notons ![]()
![]() …,
…, ![]() ces équations, avec
ces équations, avec ![]() qui n’est donc pas autre chose que
qui n’est donc pas autre chose que ![]()
Notons aussi ![]() l’ensemble des solutions de
l’ensemble des solutions de ![]()
L’exigence que, pour chaque ![]() on ait
on ait ![]() signifie exactement que
signifie exactement que ![]() pour chaque tel entier
pour chaque tel entier ![]() .
.
Si l’on sait seulement que ![]() pour tout
pour tout ![]() alors
alors ![]() pour tout
pour tout ![]() et par conséquent
et par conséquent ![]()
Mais cette dernière inclusion n’a aucune raison d’être une égalité. Un chaîne d’inclusion ne suffit donc pas pour déterminer ![]()
Par exemple, étant donné ![]() :
:
![]()
- celui de
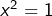 est
est 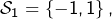
- celui de
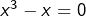 est
est 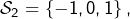
- celui de
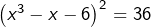 est
est 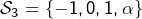 avec
avec 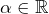 dont une valeur approchée par défaut à
dont une valeur approchée par défaut à 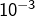 près est
près est 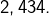
Pire : si ![]() pour certains indices
pour certains indices ![]() tandis que
tandis que ![]() pour d’autres, on ne sera pas en mesure de comparer les ensembles
pour d’autres, on ne sera pas en mesure de comparer les ensembles ![]() et
et ![]()
En revanche, si ![]() pour tout
pour tout ![]() alors
alors ![]() pour tout
pour tout ![]() et ceci garantit que
et ceci garantit que ![]()
Des remarques analogues s’appliquent à la résolution d’une inéquation.
4 – Chaînes d’équivalences
Le « squelette » de l’énoncé de certains théorèmes se présente ainsi :
Théorème XYZ
Les assertions suivantes sont équivalentes :
- Assertion
- Assertion
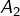
- …
- Assertion
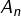
Pour établir ce genre de résultat, il serait franchement maladroit de chercher à démontrer les implications du type ![]() pour tous les couples
pour tous les couples ![]() vérifiant
vérifiant ![]() (il existe
(il existe ![]() tels couples).
tels couples).
Il est beaucoup moins « coûteux » de prouver les ![]() implications :
implications :
![]()
Donnons deux exemples. Le premier est emprunté à l’algèbre linéaire :
Caractérisation d’une somme directe
On considère un ![]() espace vectoriel
espace vectoriel ![]() et deux sous-espaces
et deux sous-espaces ![]() de
de ![]() On note
On note ![]() qui désigne par définition l’ensemble des vecteurs de la forme
qui désigne par définition l’ensemble des vecteurs de la forme ![]() avec
avec ![]() et
et ![]()
Les trois assertions suivantes sont équivalentes :
- Tout vecteur de
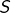 peut s’écrire d’une seule manière sous la forme
peut s’écrire d’une seule manière sous la forme 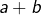 avec
avec 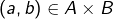
- Pour tout couple
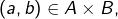 si
si 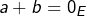 alors
alors 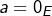 et
et 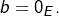
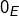 est le seul vecteur appartenant simultanément à
est le seul vecteur appartenant simultanément à 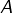 et à
et à 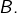
Caractérisation des applications linéaires continues
On considère deux espaces vectoriels normés réels ![]() et
et ![]() La norme d’un vecteur
La norme d’un vecteur ![]() est notée
est notée ![]() et celle d’un vecteur
et celle d’un vecteur ![]() est notée
est notée ![]() Etant donnée une application linéaire
Etant donnée une application linéaire ![]() les assertions suivantes sont équivalentes :
les assertions suivantes sont équivalentes :
 est continue
est continue est continue en
est continue en 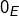
 est bornée sur la boule unité fermée de
est bornée sur la boule unité fermée de 
 est bornée sur la sphère unité de
est bornée sur la sphère unité de 
- il existe
 tel que :
tel que : 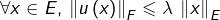
Pour le lecteur intéressé, des preuves détaillées de l’équivalence des assertions 1 à 3 de l’exemple 1 et des assertions 1 à 5 de l’exemple 2 sont données en annexe.
5 – Négation de 
Comme on l’a expliqué, la négation d’une implication ![]() équivaut logiquement à P et non(Q).
équivaut logiquement à P et non(Q).
Ceci nous indique la marche à suivre pour démontrer par l’absurde qu’une implication est vraie.
Par exemple, tâchons d’établir le résultat énoncé à la première section :
(![]() )
) ![]()
![]()
L’assertion ![]() est établie !
est établie !
Passons à un exemple plus consistant : le théorème de caractérisation séquentielle des fermés de ![]()
Avant de l’énoncer, rappelons deux définitions :
Définition 1
Une partie ![]() de
de ![]() est un ouvert lorsque pour tout
est un ouvert lorsque pour tout ![]() il existe
il existe ![]() tel que :
tel que :
![]()
Définition 2
Une partie ![]() de
de ![]() est un fermé lorsque son complémentaire
est un fermé lorsque son complémentaire ![]() est un ouvert.
est un ouvert.
Théorème
Etant donnée une partie ![]() de
de ![]() les assertions suivantes sont équivalentes :
les assertions suivantes sont équivalentes :
(1) ![]() est un fermé.
est un fermé.
(2) Pour tout suite convergente à termes dans ![]() la limite de cette suite appartient à
la limite de cette suite appartient à ![]()
Ce théorème pourrait être énoncé dans un cadre plus général (en se plaçant non pas dans ![]() , mais dans un quelconque espace métrique) et la preuve n’en serait essentiellement pas modifiée.
, mais dans un quelconque espace métrique) et la preuve n’en serait essentiellement pas modifiée.
On démontre chacune des deux implications ![]() et
et ![]() en raisonnant par l’absurde.
en raisonnant par l’absurde.
![]() Supposons (1) et non (2), c’est-à-dire que
Supposons (1) et non (2), c’est-à-dire que ![]() est un fermé et qu’il existe une suite
est un fermé et qu’il existe une suite ![]() à termes dans
à termes dans ![]() qui converge vers un réel
qui converge vers un réel ![]()
Comme ![]() est ouvert, il existe
est ouvert, il existe ![]() tel que
tel que ![]() autrement dit : l’intervalle
autrement dit : l’intervalle ![]() ne contient aucun élément de
ne contient aucun élément de ![]()
Par ailleurs, il existe un entier ![]() tel que
tel que ![]() pour tout entier
pour tout entier ![]() On voit donc
On voit donc ![]() dès que
dès que ![]() ce qui est absurde puisque
ce qui est absurde puisque ![]()
![]() Supposons (2) et non (1), c’est-à-dire, d’une part, que la limite de toute suite convergente à termes dans
Supposons (2) et non (1), c’est-à-dire, d’une part, que la limite de toute suite convergente à termes dans ![]() appartient à
appartient à ![]() et, d’autre part, que
et, d’autre part, que ![]() n’est pas un fermé (ce qui signifie que
n’est pas un fermé (ce qui signifie que ![]() n’est pas un ouvert). Il existe alors
n’est pas un ouvert). Il existe alors ![]() tel que pour tout
tel que pour tout ![]() on a
on a ![]()
D’après ce dernier point on peut, pour tout ![]() choisir un élément
choisir un élément ![]() tel que
tel que ![]()
Il est alors clair que la suite ![]() est à termes dans
est à termes dans ![]() et converge vers
et converge vers ![]() Et comme
Et comme ![]() n’appartient pas à
n’appartient pas à ![]() on aboutit à une contradiction !
on aboutit à une contradiction !
6 – Contraposée de 
Imaginons qu’une personne travaillant dans une agence de voyage nous dise, à propos d’un passager :
Si ce passager a pu prendre son vol normalement,
alors son passeport est en règle
Chacun comprendra que cette phrase possède la même signification que :
Si le passeport de ce passager n’est pas en règle,
alors il n’a pas pu prendre son vol normalement
D’une manière générale, une implication ![]() peut être remplacée par sa contraposée, à savoir l’implication
peut être remplacée par sa contraposée, à savoir l’implication ![]()
Les deux implications sont formellement distinctes mais sont logiquement équivalentes (elles ont la même valeur de vérité).
Attention de ne pas confondre « contraposée » et « négation » : la contraposée d’une implication dit la même chose que l’implication initiale, tandis que la négation exprime le contraire !
Voici quatre exemples qui vous permettront, j’espère, d’y voir plus clair …
Exemple 1 : une simple question de parité
Etant donné un entier naturel ![]() si
si ![]() est pair alors
est pair alors ![]() est pair.
est pair.
Il est facile de prouver l’implication contraposée, à savoir : si ![]() est impair, alors
est impair, alors ![]() est impair.
est impair.
En effet, un entier impair ![]() peut s’écrire sous la forme
peut s’écrire sous la forme ![]() avec
avec ![]() On voit alors que
On voit alors que
![]()
Exemple 2 : le théorème de Pythagore
Etant donnés trois points ![]() non alignés, le théorème de Pythagore stipule que si le triangle
non alignés, le théorème de Pythagore stipule que si le triangle ![]() est rectangle en
est rectangle en ![]() alors
alors ![]() On peut énoncer le même résultat sous forme contraposée, en affirmant que si
On peut énoncer le même résultat sous forme contraposée, en affirmant que si ![]() alors le triangle
alors le triangle ![]() n’est certainement pas rectangle en
n’est certainement pas rectangle en ![]()
Exemple 3 : à propos de l’injectivité
Une application ![]() est dite injective lorsque
est dite injective lorsque
![]()
Etablir l’injectivité d’une application avec cette formulation peut être malaisé dans certains cas, car la relation ![]() ne possède pas de bonnes propriétés, contrairement à la relation d’égalité (voir à ce sujet l’article Injections & Surjections : méthodes).
ne possède pas de bonnes propriétés, contrairement à la relation d’égalité (voir à ce sujet l’article Injections & Surjections : méthodes).
En effet, l’égalité est transitive : si ![]() et
et ![]() alors
alors ![]() Tandis que
Tandis que ![]() et
et ![]() mais on ne va tout de même pas en déduire que
mais on ne va tout de même pas en déduire que ![]()
En outre, deux égalités entre nombres réels peuvent être ajoutées membre-à-membre : si ![]() et
et ![]() alors
alors ![]() Mais
Mais ![]() et
et ![]() et il n’est pas question d’en déduire que
et il n’est pas question d’en déduire que ![]()
Bref, il est généralement (quoique pas toujours…) plus commode de passer par la forme contraposée et donc, d’exprimer l’injectivité de ![]() en écrivant :
en écrivant :
![]()
Exemple 4 : une question d’algèbre linéaire
Soit ![]() un espace vectoriel de dimension finie et soient
un espace vectoriel de dimension finie et soient ![]() deux sous-espaces vectoriels de
deux sous-espaces vectoriels de ![]()
Si ![]() alors
alors ![]()
On établit la contraposée, c’est-à-dire : si ![]() alors
alors ![]()
En effet, si ![]() alors la somme
alors la somme ![]() est directe et donc :
est directe et donc :
![]()
![]()
![]()
7 – Réciproque de 
Lorsqu’un(e) mathématicien(ne) démontre une implication ![]() il (ou elle)ne peut pas s’empêcher de se demander si l’implication
il (ou elle)ne peut pas s’empêcher de se demander si l’implication ![]() est aussi vraie .
est aussi vraie .
On dit que ![]() est la réciproque de
est la réciproque de ![]()
Certains affirment, à ce sujet (et en ne plaisantant qu’à moitié) que plus une implication est banale et évidente, plus sa réciproque (si toutefois elle est vraie…) est intéressante et peut même, dans certains cas, constituer un résultat profond.
Commençons par un exemple totalement élémentaire.
Exemple 1 : factorisation d’un polynôme dont une racine est connue
Soit ![]() une fonction polynôme et soit
une fonction polynôme et soit ![]()
S’il existe une fonction polynôme ![]() telle que
telle que ![]() alors
alors ![]()
C’est évident !! La réciproque est-elle vraie ? Affirmatif :
Si ![]() , alors il existe une fonction polynôme
, alors il existe une fonction polynôme ![]() telle que
telle que ![]()
Autrement dit, il est possible de factoriser ![]() par
par ![]() Ceci se prouve facilement à l’aide de l’identité
Ceci se prouve facilement à l’aide de l’identité 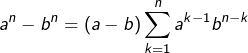 (voir par exemple cet article) ou bien, si l’on préfère, en effectuant la division euclidienne du polynôme
(voir par exemple cet article) ou bien, si l’on préfère, en effectuant la division euclidienne du polynôme ![]() par le polynôme
par le polynôme ![]() (le reste est un polynôme constant qui donne
(le reste est un polynôme constant qui donne ![]() lorsqu’on l’évalue en
lorsqu’on l’évalue en ![]()
Exemple 2 : le théorème des trois carrés
Il n’est pas très difficile de prouver que si un entier naturel ![]() est la somme de trois carrés parfaits, alors
est la somme de trois carrés parfaits, alors ![]() n’est pas de la forme
n’est pas de la forme ![]()
En effet, on sait qu’un carré parfait est congru, modulo 8, à l’un des trois entiers 0, 1 ou 4.
Par conséquent, si l’on ajoute trois carrés parfaits, on obtient un entier congru à :
![Rendered by QuickLaTeX.com \[\begin{matrix}0+0+0 & \equiv & 0\pmod{8}\\0+0+1 & \equiv & 1\pmod{8}\\0+0+4 & \equiv & 4\pmod{8}\\0+1+1 & \equiv & 2\pmod{8}\\0+1+4 & \equiv & 5\pmod{8}\\0+4+4 & \equiv & 0\pmod{8}\\1+1+1 & \equiv & 3\pmod{8}\\1+1+4 & \equiv & 6\pmod{8}\\1+4+4 & \equiv & 1\pmod{8}\\& \text{ou}\\4+4+4 & \equiv & 4\pmod{8}\end{matrix}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-23a93cd866dbd90403208640cb93d5aa_l3.png)
On observe donc qu’une somme de trois carrés n’est, en aucun cas, congrue à ![]() modulo
modulo ![]()
On en déduit que si ![]() pouvait s’écrire sous la forme
pouvait s’écrire sous la forme ![]() alors il faudrait que
alors il faudrait que ![]() Mais on aurait alors
Mais on aurait alors ![]() ce qui imposerait
ce qui imposerait ![]() et
et ![]() tous pairs, d’où la possibilité en divisant par
tous pairs, d’où la possibilité en divisant par ![]() , d’écrire :
, d’écrire :
![]()
Il se trouve que la réciproque est vraie : tout entier naturel qui n’est pas de la forme ![]() peut s’écrire comme la somme de trois carrés parfaits ! Ce résultat, dû à Gauss, constitue le théorème des trois carrés et sa démonstration n’est pas commode.
peut s’écrire comme la somme de trois carrés parfaits ! Ce résultat, dû à Gauss, constitue le théorème des trois carrés et sa démonstration n’est pas commode.
Exemple 3 : la conjecture de Goldbach forte
Il est évident que si un entier naturel ![]() est la somme de deux nombres premiers impairs, alors
est la somme de deux nombres premiers impairs, alors ![]() est pair et
est pair et ![]() La réciproque de cette implication consiste à dire que tout entier pair, supérieur ou égal à
La réciproque de cette implication consiste à dire que tout entier pair, supérieur ou égal à ![]() est la somme de deux nombres premiers impairs. Mais cette affirmation constitue à ce jour une redoutable question ouverte (c’est la conjecture de Goldbach « forte » ou « binaire » par contraste avec la conjecture de Goldbach « faible » ou « ternaire », selon laquelle tout nombre impair
est la somme de deux nombres premiers impairs. Mais cette affirmation constitue à ce jour une redoutable question ouverte (c’est la conjecture de Goldbach « forte » ou « binaire » par contraste avec la conjecture de Goldbach « faible » ou « ternaire », selon laquelle tout nombre impair ![]() est la somme de trois nombres premiers, résultat extrêmement difficile, établi en 2013 par le mathématicien péruvien Harald Helfgott).
est la somme de trois nombres premiers, résultat extrêmement difficile, établi en 2013 par le mathématicien péruvien Harald Helfgott).

Signalons une curiosité : il arrive parfois qu’on ait à démontrer une équivalence entre deux assertions, mais que la preuve de l’une des deux implications « contienne », en un sens, celle de sa réciproque. Deux exemples de cette situation sont détaillés dans cet article.
8 – Réciproques partielles
Bien entendu, il arrive parfois qu’une implication ![]() soit vraie mais que sa réciproque soit fausse.
soit vraie mais que sa réciproque soit fausse.
On peut alors chercher ce qu’on appelle une « réciproque partielle » :
On remplace ![]() par
par ![]() où
où ![]() désigne une hypothèse supplémentaire convenable, qui vient en quelque sorte renforcer l’hypothèse
désigne une hypothèse supplémentaire convenable, qui vient en quelque sorte renforcer l’hypothèse ![]() , insuffisante.
, insuffisante.
Voici deux exemples. Le premier est très simple :
Exemple 1 : annulation d’une fonction numérique
Etant donnée une application ![]() intéressons-nous aux deux assertions :
intéressons-nous aux deux assertions :
L’implication ![]() est évidemment vraie. Mais sa réciproque est fausse, comme on le voit en considérant l’application
est évidemment vraie. Mais sa réciproque est fausse, comme on le voit en considérant l’application
![]()
On obtient une réciproque partielle en ajoutant une hypothèse de continuité. En effet, si ![]() est continue et vérifie
est continue et vérifie ![]() alors de deux choses l’une : ou bien l’une des deux inégalités est une égalité et c’est réglé, ou bien les deux inégalités sont strictes et on peut alors conclure avec le théorème des valeurs intermédiaires.
alors de deux choses l’une : ou bien l’une des deux inégalités est une égalité et c’est réglé, ou bien les deux inégalités sont strictes et on peut alors conclure avec le théorème des valeurs intermédiaires.
Exemple 2 : moyenne de Cesàro
Il est classique que si une suite réelle ![]() converge vers une limite L, alors la suite de terme général
converge vers une limite L, alors la suite de terme général
![Rendered by QuickLaTeX.com \[M_{n}=\frac{1}{n}\sum_{k=1}^{n}u_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e785c10d2cfb8aaf00ff0eeb20476295_l3.png)
La réciproque est fausse, comme le montre l’exemple de la suite définie par :
![]()
![Rendered by QuickLaTeX.com \[M_{n}=\frac{1}{n}\sum_{k=1}^{n}\left(-1\right)^{k}=\frac{\left(-1\right)^{n}-1}{2n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3938da460abf41b463a5fb583ad5ebf4_l3.png)
Une réciproque partielle est obtenue en ajoutant à l’hypothèse de convergence de la suite ![]() celle de monotonie de la suite
celle de monotonie de la suite ![]() Montrons cela.
Montrons cela.
Quitte à remplacer la suite ![]() par la suite opposée (de terme général
par la suite opposée (de terme général ![]() on peut supposer
on peut supposer ![]() croissante. On observe alors que, pour tout
croissante. On observe alors que, pour tout ![]() :
:
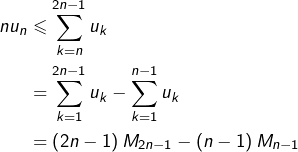
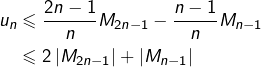
On peut d’ailleurs ajouter que sa limite est nécessairement égale à celle de la suite ![]() (en raison du théorème de Cesàro dans le sens direct !… et de la propriété d’unicité de la limite d’une suite convergente).
(en raison du théorème de Cesàro dans le sens direct !… et de la propriété d’unicité de la limite d’une suite convergente).
Annexe
On détaille ici la preuve de chacune des deux chaînes d’équivalences énoncées à la section 4.
Caractérisation d’une somme directe
![]()
Soient ![]() et
et ![]() tels que
tels que ![]() Vue l’hypothèse d’unicité, l’égalité :
Vue l’hypothèse d’unicité, l’égalité :
![]()
![]()
Soit ![]() On constate que :
On constate que :
![]()
![]()
Soient ![]() et
et ![]() tels que :
tels que :
![]()
![]()
![]()
Caractérisation des applications linéaires continues
![]()
Cette implication est triviale : la continuité de ![]() entraîne évidemment sa continuité en
entraîne évidemment sa continuité en ![]()
![]()
Il existe par hypothèse ![]() tel que, pour tout
tel que, pour tout ![]() :
:
![]()
![]()
![]()
![]()
C’est évident car la sphère unité de ![]() est incluse dans la boule unité fermé de
est incluse dans la boule unité fermé de ![]()
![]()
Par hypothèse, il existe ![]() tel que :
tel que :
![]()
![]()
![]()
![]()
Pour tout ![]() :
:
![]()
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

C’est extrêmement profitable !
Bonsoir Monsieur,
Merci pour cet article.
J’avais vu en devoir maison de MPSI le théorème des deux carrés, mais je ne connaissais pas le théorème des trois carrés !
Sauf erreurs de ma part, j’ai relevé quelques petites coquilles:
-Fin de la partie 3, après le « pire » en rouge: la deuxième implication voulue est peut-être la réciproque de la première (la première est répétée deux fois);
-Partie 4 définition 1: le code latex de l’intervalle avec les epsilon ne s’affiche pas correctement;
-Partie 4 dans la preuve du théorème, pour la deuxième implication: ce serait « différent » plutôt que « égal » à l’ensemble vide;
-Partie 6 dans les dernières inégalités de l’exemple 4: ce serait dim(F+G) à la place de dim(F inter G), et dim(F inter G) à la place de dim(F) + dim (G);
-Tout à la fin de la partie 7, un article est mentionné -Viser la cible- suivi de « Nous y avons vu… », or le résultat de convexité cité n’est pas dans cet article, ainsi vous souhaitiez peut-être faire un renvoi vers un autre article;
-Dans l’annexe, pour le (2) implique (3) de la première chaîne d’équivalences, entre parenthèses ce serait -x « égal » au lieu de « appartient ».
Bien à vous.
Vous avez raison sur toute la ligne ! Je vous remercie vivement pour cette nouvelle lecture millimétrique, qui contribue à améliorer ces articles en y détectant toutes ces petites coquilles. Il est amusant de constater à quel point le cerveau « corrige » certaines fautes de frappe : il me faut parfois relire trois ou quatre fois un même passage avant de constater que tel symbole n’est pas le bon (et que malgré moi, je lisais autre chose que ce qui était écrit !).
Quant à l’exemple soi-disant développé dans l’article « Viser la cible ! », je ne comprends pas … j’aurais juré l’avoir rédigé. Je ferai le nécessaire sous peu.
Je viens de modifier le texte de l’article « Viser la cible ! », qui comporte désormais deux exemples au lieu d’un seul, à la section 4 (section dont j’ai aussi modifié le nom …). J’espère que c’est à présent en place.
Je viens de relire « viser la cible » et tout est en place 😊
Je me demandais, avez-vous déjà eu un élève ayant une certaine maturité (ou de façon plus générale une personne ayant un bon niveau de Sup voire un niveau correct de Spé), qui vous a demandé un conseil de livre proposant de belles aventures mathématiques ? Le cas échéant, quel(s) livre(s) conseillez-vous ?
(Je pense notamment à « Raisonnements divins » traduction de « Proofs from the book », ou encore « Introduction à la théorie des nombres » de G.H.Hardy traduit par F.Sauvageot)
Bien à vous
Bonsoir, pouvez-vous revoir le passage avec la contraposée et la négation …? Il y a une répétition du mot « contraposée » et absence de « négation ». Du coup, le paragraphe ne semble pas avoir de sens… merci
Bien vu ! C’est corrigé … Et merci pour votre lecture attentive.