Lettre C
CANONIQUE (base)
Commençons par un point important, souvent mal compris : étant donné un ![]() espace vectoriel E abstrait, de dimension finie, l’expression base canonique de E n’a AUCUN sens !
espace vectoriel E abstrait, de dimension finie, l’expression base canonique de E n’a AUCUN sens !
En revanche, cette expression est bien définie lorsque ![]() est
est ![]() où bien
où bien ![]() (espace des polynômes de degré inférieur où égal
(espace des polynômes de degré inférieur où égal ![]() ou encore
ou encore ![]() (espace des matrices rectangulaires à
(espace des matrices rectangulaires à ![]() lignes et
lignes et ![]() colonnes) :
colonnes) :
La base canonique de ![]() est :
est :
![]()
![]()
![]()
Par exemple, la base canonique de
![]()
CARDINAL
Le cardinal d’un ensemble fini ![]() est simplement le nombre d’éléments de
est simplement le nombre d’éléments de ![]() .
.
On le note : ![]() .
.
Par exemple, si ![]() , alors
, alors ![]() .
.
Pour être plus précis, on peut définir cette notion comme suit :
- l’ensemble vide est de cardinal 0
- si
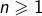 , un ensemble est dit de cardinal
, un ensemble est dit de cardinal  lorsqu’il est en bijection avec
lorsqu’il est en bijection avec 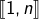
La validité de cette définition résulte du fait que si ![]() sont deux entiers naturels non nuls tels que
sont deux entiers naturels non nuls tels que ![]() et
et ![]() sont en bijection, alors
sont en bijection, alors ![]() .
.
Si ![]() sont deux ensembles finis et disjoints, alors :
sont deux ensembles finis et disjoints, alors :
![]()
![]()
On peut encore généraliser … pour obtenir la formule du crible, qui donne le cardinal d’une union finie d’ensembles finis.
La notion de cardinal s’étend aux cas des ensembles infinis, mais cette notion est plus délicate. Disons, sans rentrer dans les détails, que le cardinal d’un ensemble ![]() peut être défini comme la classe (propre) des ensembles équipotents à
peut être défini comme la classe (propre) des ensembles équipotents à ![]() (c’est-à-dire : des ensembles qui sont en bijection avec
(c’est-à-dire : des ensembles qui sont en bijection avec ![]() ).
).
CAUCHY-SCHWARZ (inégalité de)
Définition
Etant donné un ![]() espace vectoriel
espace vectoriel ![]() on appelle forme bilinéaire symétrique positive (FBSP) sur
on appelle forme bilinéaire symétrique positive (FBSP) sur ![]() toute application
toute application ![]() telle que, pour tout
telle que, pour tout ![]() :
:
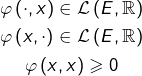
![]()
On note classiquement ![]() l’application partielle
l’application partielle ![]()
Notation analogue pour ![]()
![]() désigne l’espace des formes linéaires sur
désigne l’espace des formes linéaires sur ![]()
Théorème (inégalité de Cauchy-Schwarz)
Etant donnés un ![]() espace vectoriel
espace vectoriel ![]() et une FBSP sur
et une FBSP sur ![]() :
:
(CS) ![]()
Bien entendu, ce résultat est aussi valable :
- si
 est une forme bilinéaire symétrique négative.
est une forme bilinéaire symétrique négative. - si
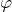 est un produit scalaire (FBS définie positive).
est un produit scalaire (FBS définie positive).
On peut montrer que les FBS qui satisfont (CS) sont exactement les FBSP et leurs opposées.
Voici trois versions particulières usuelles de (CS) :
Exemple 1
Pour tout ![]() et pour tous
et pour tous ![]() et
et ![]() :
:
![Rendered by QuickLaTeX.com \[\left(\sum_{i=1}^{n}x_{i}y_{i}\right)^{2}\leqslant\left(\sum_{i=1}^{n}x_{i}^{2}\right)\left(\sum_{i=1}^{n}y_{i}^{2}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7ec3b0380dea4c9c71dd755ec30373be_l3.png)
Exemple 2
Pour tout couple ![]() d’applications continues par morceaux de
d’applications continues par morceaux de ![]() dans
dans ![]() :
:
![Rendered by QuickLaTeX.com \[\left(\int_{a}^{b}f\left(t\right)\thinspace g\left(t\right)\thinspace dt\right)^{2}\leqslant\left(\int_{a}^{b}f\left(t\right)^{2}\thinspace dt\right)\left(\int_{a}^{b}g\left(t\right)^{2}\thinspace dt\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5129eb8a7b47d2b6b593d9340b2b8812_l3.png)
Exemple 3
Si ![]() est un espace probabilisé et si
est un espace probabilisé et si ![]() est un couple de variables aléatoires réelles possédant une variance, alors :
est un couple de variables aléatoires réelles possédant une variance, alors :
![]()
A toute FBSP est associée une semi-norme, définie par :
![]()
Bien sûr, cette semi-norme devient une norme à part entière si ![]() est un produit scalaire.
est un produit scalaire.
Définition
Etant donné un ![]() espace vectoriel
espace vectoriel ![]() on appelle forme bilinéaire symétrique positive (FBSP) sur
on appelle forme bilinéaire symétrique positive (FBSP) sur ![]() toute application
toute application ![]() telle que, pour tout
telle que, pour tout ![]() :
:
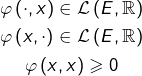
![]()
On note classiquement ![]() l’application partielle
l’application partielle ![]()
Notation analogue pour ![]()
![]() désigne l’espace des formes linéaires sur
désigne l’espace des formes linéaires sur ![]()
Théorème (inégalité de Cauchy-Schwarz)
Etant donnés un ![]() espace vectoriel
espace vectoriel ![]() et une FBSP sur
et une FBSP sur ![]() :
:
(CS) ![]()
Bien entendu, ce résultat est aussi valable :
- si
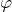 est une forme bilinéaire symétrique négative.
est une forme bilinéaire symétrique négative. - si
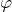 est un produit scalaire (FBS définie positive).
est un produit scalaire (FBS définie positive).
On peut montrer que les FBS qui satisfont (CS) sont exactement les FBSP et leurs opposées.
Voici trois versions particulières usuelles de (CS) :
Exemple 1
Pour tout ![]() et pour tous
et pour tous ![]() et
et ![]() :
:
![Rendered by QuickLaTeX.com \[\left(\sum_{i=1}^{n}x_{i}y_{i}\right)^{2}\leqslant\left(\sum_{i=1}^{n}x_{i}^{2}\right)\left(\sum_{i=1}^{n}y_{i}^{2}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7ec3b0380dea4c9c71dd755ec30373be_l3.png)
Exemple 2
Pour tout couple ![]() d’applications continues par morceaux de
d’applications continues par morceaux de ![]() dans
dans ![]() :
:
![Rendered by QuickLaTeX.com \[\left(\int_{a}^{b}f\left(t\right)\thinspace g\left(t\right)\thinspace dt\right)^{2}\leqslant\left(\int_{a}^{b}f\left(t\right)^{2}\thinspace dt\right)\left(\int_{a}^{b}g\left(t\right)^{2}\thinspace dt\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5129eb8a7b47d2b6b593d9340b2b8812_l3.png)
Exemple 3
Si ![]() est un espace probabilisé et si
est un espace probabilisé et si ![]() est un couple de variables aléatoires réelles possédant une variance, alors :
est un couple de variables aléatoires réelles possédant une variance, alors :
![]()
A toute FBSP est associée une semi-norme, définie par :
![]()
Bien sûr, cette semi-norme devient une norme à part entière si ![]() est un produit scalaire.
est un produit scalaire.
Remarque
Dans le cas particulier d’un espace préhilbertien réel (espace vectoriel réel muni d’un produit scalaire), on peut ajouter :
- que le cas d’égalité dans l’inégalité (CS) est celui ou la famille
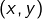 est liée,
est liée, - que (CS) entraîne la continuité du produit scalaire. En conséquence, si
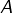 est une partie quelconque de
est une partie quelconque de 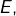 son orthogonal est fermé (comme intersection d’une famille d’hyperplans fermés).
son orthogonal est fermé (comme intersection d’une famille d’hyperplans fermés).
CESÀRO (lemme de)
Lemme de Cesàro discret
Si une suite réelle ![]() possède une limite (finie ou infinie), alors la suite de terme général
possède une limite (finie ou infinie), alors la suite de terme général
![Rendered by QuickLaTeX.com \[M_{n}=\frac{1}{n+1}\sum_{k=0}^{n}x_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f4cacb4170154a3750b999c34989e858_l3.png)
On montre ce résultat en revenant à la définition de la convergence (ou de la divergence vers l’infini) d’une suite réelle. Une preuve détaillée est disponible dans cet article.
Sa réciproque est fausse, comme on peut le voir avec la suite de terme général ![]() En effet, la suite
En effet, la suite ![]() converge vers 0, mais la suite
converge vers 0, mais la suite ![]() diverge.
diverge.
On dispose toutefois d’une réciproque partielle :
Si la suite ![]() converge et si la suite
converge et si la suite ![]() est monotone, alors la suite
est monotone, alors la suite ![]() converge aussi (et les limites sont fatalement égales). Davantage de détails à lire ici.
converge aussi (et les limites sont fatalement égales). Davantage de détails à lire ici.
Le théorème de sommation des équivalents apporte une généralisation au lemme de Cesàro :
Si les suites à termes positifs ![]() et
et ![]() sont équivalentes, alors les séries
sont équivalentes, alors les séries ![]() et
et ![]() sont de même nature; en outre :
sont de même nature; en outre :
- En cas de convergence :
![Rendered by QuickLaTeX.com \[\sum_{k=n}^{\infty}x_{k}\sim\sum_{k=n}^{\infty}y_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ddd72dd31c3e72def78f84605a7ea528_l3.png)
- En cas de divergence :
![Rendered by QuickLaTeX.com \[\sum_{k=0}^{n}x_{k}\sim\sum_{k=0}^{n}y_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7a881b3318d827deaab7ac9610319133_l3.png)
En supposant la convergence de la suite ![]() vers une limite
vers une limite ![]() et en choisissant
et en choisissant ![]() on retrouve le lemme de Cesàro énoncé au début.
on retrouve le lemme de Cesàro énoncé au début.
Signalons aussi le :
Lemme de Cesàro, version continue
Etant donnée une application continue ![]() si
si ![]() admet en
admet en ![]() une limite
une limite ![]() (finie ou non) alors :
(finie ou non) alors :![]()
Là encore, la réciproque est fausse. Par exemple :
![]()
mais la fonction cosinus ne possède pas de limite en ![]()
Un article dédié à l’histoire du lemme de Cesàro est consultable ici.
COMMUTATIVITÉ
Une opération ![]() définie sur un ensemble
définie sur un ensemble ![]() est dite commutative lorsque
est dite commutative lorsque
![]()
Par exemple, sont commutatives les opérations suivantes :
- addition et multiplication dans
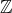
- union et intersection dans
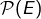 (ensemble des parties de
(ensemble des parties de  )
) - pgcd et ppcm dans
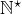
En revanche, les opérations ci-dessous ne sont pas commutatives :
- soustraction dans
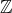
- division dans
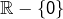
En effet : ![]() et
et ![]()
Un groupe dont l’opération est commutative est dit abélien.
COMPACT
Un espace topologique ![]() est dit compact s’il est séparé (pour tout couple
est dit compact s’il est séparé (pour tout couple ![]() de points distincts de
de points distincts de ![]() on peut trouver deux ouverts
on peut trouver deux ouverts ![]() disjoints, tels que
disjoints, tels que ![]() et
et ![]() ) et si l’on peut extraire de tout recouvrement ouvert de
) et si l’on peut extraire de tout recouvrement ouvert de ![]() un sous-recouvrement fini.
un sous-recouvrement fini.
Cette dernière condition signifie que pour toute famille ![]() d’ouverts vérifiant
d’ouverts vérifiant ![]() il existe
il existe ![]() tel que
tel que ![]() est fini et
est fini et ![]()
On peut montrer que, pour un espace métrique ![]() (et, en particulier pour un espace vectoriel normé), cette définition équivaut à la suivante (appelée compacité séquentielle) : de toute suite à termes dans
(et, en particulier pour un espace vectoriel normé), cette définition équivaut à la suivante (appelée compacité séquentielle) : de toute suite à termes dans ![]() on peut extraire une sous-suite convergente.
on peut extraire une sous-suite convergente.
Etant donné d’un espace métrique ![]() :
:
- toute partie compacte de
 est fermée.
est fermée. - si
 est compact, alors toute partie fermée de
est compact, alors toute partie fermée de  est compacte.
est compacte. - si
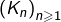 est une suite décroissante de parties compactes non vides, alors
est une suite décroissante de parties compactes non vides, alors 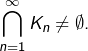
Etant donnés deux espaces métriques ![]() :
:
- si
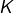 est une partie compacte de
est une partie compacte de  et si
et si 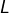 est une partie compacte de
est une partie compacte de 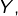 alors
alors 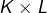 est une partie compacte de
est une partie compacte de 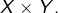
- si
 est compact et si
est compact et si 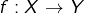 est continue, alors
est continue, alors 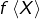 est une partie compacte de
est une partie compacte de 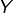 (énoncé
(énoncé  ).
).
Dans un espace vectoriel normé de dimension finie, les parties compactes sont celles qui sont fermées et bornées.
Cas particulier de l’énoncé ![]() : toute application continue d’un métrique compact dans
: toute application continue d’un métrique compact dans ![]() est bornée et atteint ses bornes. Ceci généralise le théorème selon lequel toute application continue
est bornée et atteint ses bornes. Ceci généralise le théorème selon lequel toute application continue ![]() est bornée et atteint ses bornes (en effet : un segment est une partie fermée et bornée de
est bornée et atteint ses bornes (en effet : un segment est une partie fermée et bornée de ![]() , donc un espace compact).
, donc un espace compact).
Exemple 1
Etant donné un ![]() evn
evn ![]() notons
notons ![]() sa boule unité fermée et
sa boule unité fermée et ![]() sa sphère unité. Alors la compacité de
sa sphère unité. Alors la compacité de ![]() et celle de
et celle de ![]() sont équivalentes. En effet, si la sphère
sont équivalentes. En effet, si la sphère ![]() est compacte, alors comme l’application :
est compacte, alors comme l’application :
![]()
Exemple 2
Dans ![]() étant donné un triangle
étant donné un triangle ![]() (enveloppe convexe de trois points
(enveloppe convexe de trois points ![]() non alignés), il existe un point
non alignés), il existe un point ![]() en lequel le produit
en lequel le produit ![]() est maximum. Il suffit de voir que
est maximum. Il suffit de voir que ![]() est compact (fermé et borné) et que l’application :
est compact (fermé et borné) et que l’application :
![]()
Un espace topologique ![]() est dit compact s’il est séparé (pour tout couple
est dit compact s’il est séparé (pour tout couple ![]() de points distincts de
de points distincts de ![]() on peut trouver deux ouverts
on peut trouver deux ouverts ![]() disjoints, tels que
disjoints, tels que ![]() et
et ![]() ) et si l’on peut extraire de tout recouvrement ouvert de
) et si l’on peut extraire de tout recouvrement ouvert de ![]() un sous-recouvrement fini.
un sous-recouvrement fini.
Cette dernière condition signifie que pour toute famille ![]() d’ouverts vérifiant
d’ouverts vérifiant ![]() il existe
il existe ![]() tel que
tel que ![]() est fini et
est fini et ![]()
On peut montrer que, pour un espace métrique ![]() (et, en particulier pour un espace vectoriel normé), cette définition équivaut à la suivante (appelée compacité séquentielle) : de toute suite à termes dans
(et, en particulier pour un espace vectoriel normé), cette définition équivaut à la suivante (appelée compacité séquentielle) : de toute suite à termes dans ![]() on peut extraire une sous-suite convergente.
on peut extraire une sous-suite convergente.
Etant donné d’un espace métrique ![]() :
:
- toute partie compacte de
 est fermée.
est fermée. - si
 est compact, alors toute partie fermée de
est compact, alors toute partie fermée de  est compacte.
est compacte. - si
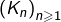 est une suite décroissante de parties compactes non vides, alors
est une suite décroissante de parties compactes non vides, alors 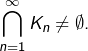
Etant donnés deux espaces métriques ![]() :
:
- si
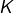 est une partie compacte de
est une partie compacte de  et si
et si 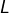 est une partie compacte de
est une partie compacte de 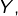 alors
alors 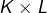 est une partie compacte de
est une partie compacte de 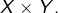
- si
 est compact et si
est compact et si 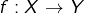 est continue, alors
est continue, alors 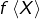 est une partie compacte de
est une partie compacte de 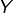 (énoncé
(énoncé  ).
).
Dans un espace vectoriel normé de dimension finie, les parties compactes sont celles qui sont fermées et bornées.
Cas particulier de l’énoncé ![]() : toute application continue d’un métrique compact dans
: toute application continue d’un métrique compact dans ![]() est bornée et atteint ses bornes. Ceci généralise le théorème selon lequel toute application continue
est bornée et atteint ses bornes. Ceci généralise le théorème selon lequel toute application continue ![]() est bornée et atteint ses bornes (en effet : un segment est une partie fermée et bornée de
est bornée et atteint ses bornes (en effet : un segment est une partie fermée et bornée de ![]() , donc un espace compact).
, donc un espace compact).
Exemple 1
Etant donné un ![]() evn
evn ![]() notons
notons ![]() sa boule unité fermée et
sa boule unité fermée et ![]() sa sphère unité. Alors la compacité de
sa sphère unité. Alors la compacité de ![]() et celle de
et celle de ![]() sont équivalentes. En effet, si la sphère
sont équivalentes. En effet, si la sphère ![]() est compacte, alors comme l’application :
est compacte, alors comme l’application :
![]()
Exemple 2
Dans ![]() étant donné un triangle
étant donné un triangle ![]() (enveloppe convexe de trois points
(enveloppe convexe de trois points ![]() non alignés), il existe un point
non alignés), il existe un point ![]() en lequel le produit
en lequel le produit ![]() est maximum. Il suffit de voir que
est maximum. Il suffit de voir que ![]() est compact (fermé et borné) et que l’application :
est compact (fermé et borné) et que l’application :
![]()
Exemple 3
Soit ![]() est un
est un ![]() evn et soient
evn et soient ![]() deux parties de
deux parties de ![]() .
.
Si ![]() est fermé et si
est fermé et si ![]() est compact, alors
est compact, alors ![]() est fermé. En effet, étant donnée une suite convergente
est fermé. En effet, étant donnée une suite convergente ![]() à termes dans
à termes dans ![]() on peut poser, pour tout
on peut poser, pour tout ![]() :
: ![]() avec
avec ![]() et
et ![]() Comme
Comme ![]() est compact, la suite
est compact, la suite ![]() possède une suite extraite
possède une suite extraite ![]() qui converge vers un vecteur
qui converge vers un vecteur ![]()
La suite ![]() est alors convergente (différence de deux suites convergentes) et, en notant
est alors convergente (différence de deux suites convergentes) et, en notant ![]() sa limite :
sa limite : ![]() car
car ![]() est fermé. En notant
est fermé. En notant ![]() la limite de
la limite de ![]() qui est aussi celle de
qui est aussi celle de ![]() on voit que :
on voit que : ![]()
COMPOSITION (loi o)
Etant donnés trois ensembles ![]() et deux applications
et deux applications ![]() et
et ![]() , on note
, on note ![]() l’application
l’application
![]()
On dit que ![]() est la composée de
est la composée de ![]() par
par ![]() .
.
On peut étendre la définition au cas où ![]() avec
avec ![]() . Cette condition garantit en effet que l’on peut appliquer
. Cette condition garantit en effet que l’on peut appliquer ![]() à
à ![]() , pour tout
, pour tout ![]() .
.
Exemple
Si ![]() et
et ![]() sont les applications suivantes :
sont les applications suivantes :
![]()
![]()
![]()
Une propriété à la fois simple et fondamentale de la composition des applications est son associativité. Cela signifie que s’il est possible de composer ![]() par
par ![]() et
et ![]() par
par ![]() , alors
, alors
![]()
Signalons pour finir que si ![]() sont deux applications d’un ensemble
sont deux applications d’un ensemble ![]() dans lui-même, alors il se peut que
dans lui-même, alors il se peut que ![]() (mais ce n’est pas vrai en général).
(mais ce n’est pas vrai en général).
On dit alors que ![]() et
et ![]() commutent.
commutent.
Etant donnés trois ensembles ![]() et deux applications
et deux applications ![]() et
et ![]() , on note
, on note ![]() l’application
l’application
![]()
On dit que ![]() est la composée de
est la composée de ![]() par
par ![]() .
.
On peut étendre la définition au cas où ![]() avec
avec ![]() . Cette condition garantit en effet que l’on peut appliquer
. Cette condition garantit en effet que l’on peut appliquer ![]() à
à ![]() , pour tout
, pour tout ![]() .
.
Exemple
Si ![]() et
et ![]() sont les applications suivantes :
sont les applications suivantes :
![]()
![]()
![]()
Une propriété à la fois simple et fondamentale de la composition des applications est son associativité. Cela signifie que s’il est possible de composer ![]() par
par ![]() et
et ![]() par
par ![]() , alors
, alors
![]()
Signalons pour finir que si ![]() sont deux applications d’un ensemble
sont deux applications d’un ensemble ![]() dans lui-même, alors il se peut que
dans lui-même, alors il se peut que ![]() (mais ce n’est pas vrai en général).
(mais ce n’est pas vrai en général).
On dit alors que ![]() et
et ![]() commutent.
commutent.
Exemple
Si ![]() , alors les polynômes de Tchebytchev de première espèce
, alors les polynômes de Tchebytchev de première espèce ![]() et
et ![]() commutent. En effet, pour tout
commutent. En effet, pour tout ![]() :
:
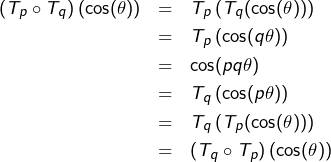
Ceci prouve que les polynômes ![]() et
et ![]() sont égaux puisqu’ils coïncident sur l’ensemble
sont égaux puisqu’ils coïncident sur l’ensemble ![]() qui est infini.
qui est infini.
CONVERGENCE (d’une suite)
Une suite réelle ![]() est dite convergente lorsqu’il existe un réel
est dite convergente lorsqu’il existe un réel ![]() tel que :
tel que :
![]()
Le réel ![]() est alors unique. C’est la limite de
est alors unique. C’est la limite de ![]() notée
notée ![]() ou bien
ou bien ![]()
Une suite non convergente est dite divergente.
Tout ce qui précède se généralise sans aucune difficulté à un espace vectoriel normé, en remplaçant valeur absolue par norme …
Exemple 1
La suite de terme général :
![Rendered by QuickLaTeX.com \[\boxed{u_{n}=\frac{2n+\left(-1\right)^{n}}{n+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-99de6548a46273c57787a3e0eb08f5cf_l3.png)
![]()
![]()
Etant donné ![]() posons :
posons :
![]()
Alors ![]() et la condition
et la condition ![]() entraîne
entraîne ![]()
Exemple 2
La suite de terme général :
![]()
En effet, supposons le contraire, notons ![]() sa limite et fixons un réel
sa limite et fixons un réel ![]()
Il existerait ![]() tel que :
tel que :
![]()
![]()
![]()
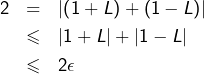
➡ On peut montrer que toute suite réelle convergente est bornée. Cet exemple montre que la réciproque est fausse.
Exemple 3
La suite de terme général :
![Rendered by QuickLaTeX.com \[\boxed{u_{n}=\left\{ \begin{array}{cc}2^{-n} & \text{si }n\text{ est pair}\\0 & \text{sinon}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8c3876a3bfce895b0b9d087d1083c12a_l3.png)
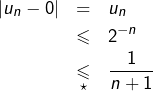
L’inégalité ![]() équivaut à
équivaut à ![]() qui se prouve aisément par récurrence.
qui se prouve aisément par récurrence.
➡ Cet exemple montre qu’une suite peut converger, sans être monotone (et même : en n’étant monotone à partir d’aucun rang). Cependant :
Théorème (limite monotone)
Toute suite réelle, croissante et majorée (ou décroissante et minorée) converge.
Toutes les opérations raisonnables entre suites réelles convergentes produisent de nouvelles suites convergentes. Notamment :
- la somme de deux suites convergentes converge vers la somme de leurs limites.
- le produit de deux suites convergentes converge vers le produit de leurs limites.
- si
 converge vers
converge vers 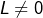 alors il existe
alors il existe 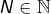 tel que
tel que 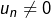 pour tout
pour tout  et, de plus, la suite
et, de plus, la suite 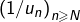 converge vers
converge vers 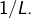
- si
 converge vers
converge vers  alors la suite de terme général :
alors la suite de terme général :
converge aussi vers![Rendered by QuickLaTeX.com \[ x_{n}=\frac{1}{n}\left(u_{0}+\cdots+u_{n-1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fcde1ca5f0492b8c5b50b223c6880280_l3.png)
 (c’est le lemme de Cesàro).
(c’est le lemme de Cesàro).
On dit que la suite réelle ![]() est de Cauchy lorsque :
est de Cauchy lorsque :
![]()
CONVEXE (fonction)
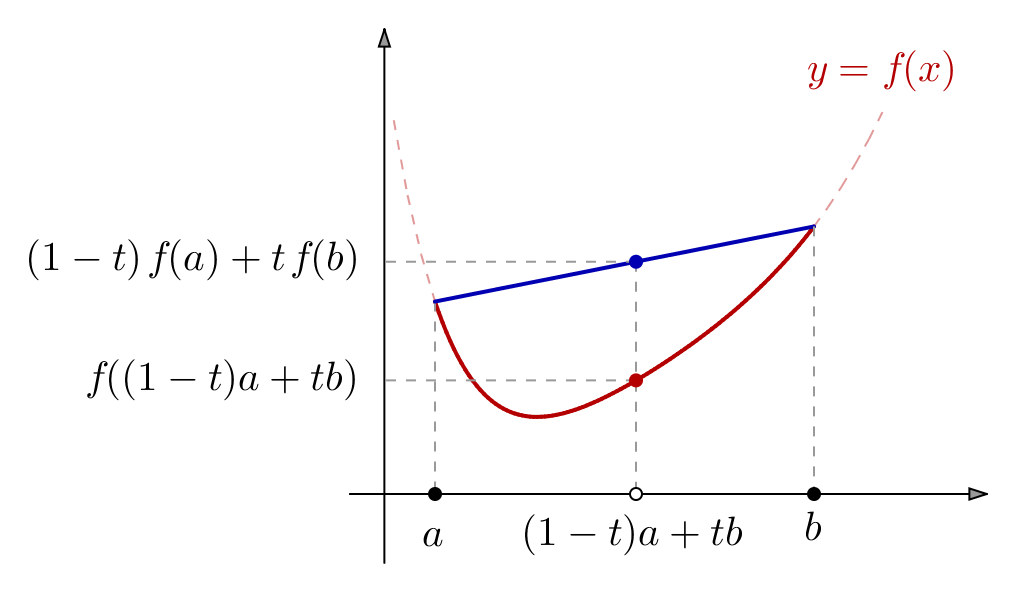
Soit ![]() un intervalle non trivial. Une application
un intervalle non trivial. Une application ![]() est dite convexe lorsque :
est dite convexe lorsque :
![]()
On dit que ![]() est concave lorsque
est concave lorsque ![]() est convexe, ce qui revient à renverser l’inégalité de définition.
est convexe, ce qui revient à renverser l’inégalité de définition.
Les applications affines sont, si l’on peut dire, à l’interface entre l’ensemble des applications convexes et celui des applications concaves (elles en forment l’intersection).
On peut montrer que si ![]() est convexe, alors
est convexe, alors ![]() est continue en tout point intérieur à
est continue en tout point intérieur à ![]() Mieux,
Mieux, ![]() est en fait dérivable à gauche et à droite en un tel point.
est en fait dérivable à gauche et à droite en un tel point.
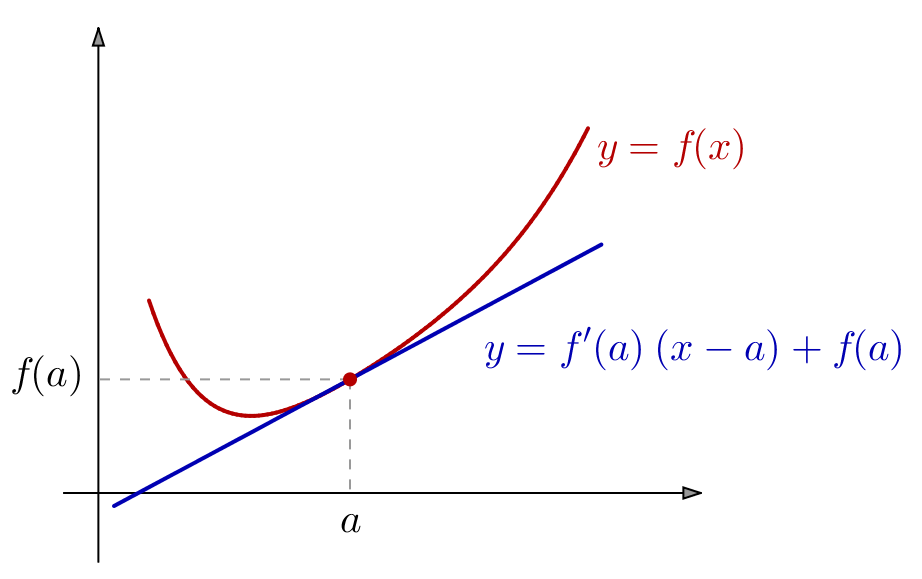
Si ![]() est dérivable, alors :
est dérivable, alors :
![]()
![]()
Exemples
Les applications ![]() pour
pour ![]() ainsi que
ainsi que ![]() pour
pour ![]() sont convexes.
sont convexes.
Le logarithme népérien est concave sur ![]()
Pour tout ![]() , l’application
, l’application ![]() est convexe sur chaque
est convexe sur chaque ![]() et concave sur chaque
et concave sur chaque ![]()
Si ![]() est dérivable est convexe, alors :
est dérivable est convexe, alors :
![]()
Comme l’exponentielle est convexe, alors :
![]()
![]()
Soit ![]() un intervalle non trivial. Une application
un intervalle non trivial. Une application ![]() est dite convexe lorsque :
est dite convexe lorsque :
![]()

On dit que ![]() est concave lorsque
est concave lorsque ![]() est convexe, ce qui revient à renverser l’inégalité de définition.
est convexe, ce qui revient à renverser l’inégalité de définition.
Les applications affines sont, si l’on peut dire, à l’interface entre l’ensemble des applications convexes et celui des applications concaves (elles en forment l’intersection).
On peut montrer que si ![]() est convexe, alors
est convexe, alors ![]() est continue en tout point intérieur à
est continue en tout point intérieur à ![]() Mieux,
Mieux, ![]() est en fait dérivable à gauche et à droite en un tel point.
est en fait dérivable à gauche et à droite en un tel point.
Si ![]() est dérivable, alors :
est dérivable, alors :
![]()
![]()

Exemples
Les applications ![]() pour
pour ![]() ainsi que
ainsi que ![]() pour
pour ![]() sont convexes.
sont convexes.
Le logarithme népérien est concave sur ![]()
Pour tout ![]() , l’application
, l’application ![]() est convexe sur chaque
est convexe sur chaque ![]() et concave sur chaque
et concave sur chaque ![]()
Si ![]() est dérivable est convexe, alors :
est dérivable est convexe, alors :
![]()

Comme l’exponentielle est convexe, alors :
![]()
![]()
Pour aller plus loin …
La notion d’application convexe se généralise.
Soit ![]() un
un ![]() espace vectoriel et
espace vectoriel et ![]() une partie convexe de
une partie convexe de ![]() Une application
Une application ![]() est dite convexe lorsque :
est dite convexe lorsque :
![]()
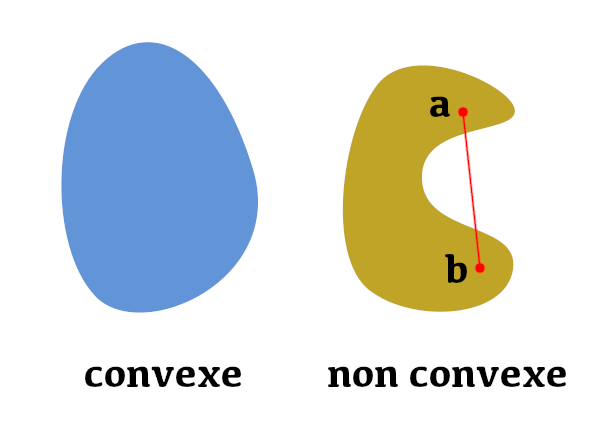
CONVEXE (partie)
Etant donné un ![]() espace vectoriel
espace vectoriel ![]() une partie
une partie ![]() de
de ![]() est dite convexe lorsque :
est dite convexe lorsque :
![Rendered by QuickLaTeX.com \[\boxed{\begin{array}{c}\forall\left(a,b\right)\in A^{2},\thinspace\forall t\in\left[0,1\right]\\\left(1-t\right)a+tb\in A\end{array}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c5852b6ec8b8789e2b61e6e7a1f9f540_l3.png)
Par définition, le segment joignant deux vecteurs ![]() est l’ensemble
est l’ensemble
![]()
Les parties convexes de ![]() sont les intervalles.
sont les intervalles.
Tout sous espace affine (et, en particulier, tout sous-espace vectoriel) de ![]() est convexe, de même que l’image directe ou réciproque d’une partie convexe par une application affine.
est convexe, de même que l’image directe ou réciproque d’une partie convexe par une application affine.
L’intersection d’une famille quelconque de parties convexes de ![]() est encore convexe. Ceci permet d’ailleurs de définir l’enveloppe convexe d’une partie quelconque
est encore convexe. Ceci permet d’ailleurs de définir l’enveloppe convexe d’une partie quelconque ![]() de
de ![]() comme l’intersection de la famille des parties convexes qui contiennent
comme l’intersection de la famille des parties convexes qui contiennent ![]()
➡ On suppose maintenant que ![]() est muni d’une norme.
est muni d’une norme.
- Toute boule (ouverte ou fermée), pour une quelconque norme sur
 est une partie convexe (ceci généralise ce qui a été dit plus haut au sujet des intervalles de
est une partie convexe (ceci généralise ce qui a été dit plus haut au sujet des intervalles de 
- L’adhérence et l’intérieur d’une partie convexe sont encore convexes.
- La distance à une partie non vide
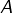 est définie par :
est définie par :
Si![Rendered by QuickLaTeX.com \[E\rightarrow\mathbb{R}^{+},\thinspace x\mapsto d_{A}\left(x\right)=\inf\left\{ \left\Vert x-a\right\Vert ;\thinspace a\in A\right\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bfc5f076a9b7caee3f263d232a162dde_l3.png)
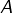 est convexe, alors l’application
est convexe, alors l’application 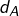 est convexe.
est convexe.
CORPS
Un corps est un anneau commutatif non nul, dont les éléments non nuls sont tous inversibles.
Autrement dit, un corps est un triplet ![]() où
où ![]() est un ensemble comportant au moins deux éléments, muni de deux opérations
est un ensemble comportant au moins deux éléments, muni de deux opérations ![]() et
et ![]() vérifiant les conditions suivantes :
vérifiant les conditions suivantes :
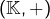 est un groupe (donc l’élément neutre est noté 0)
est un groupe (donc l’élément neutre est noté 0) est associative, commutative et distributive sur
est associative, commutative et distributive sur 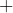
- il existe un élément neutre pour
 , noté 1
, noté 1 - tout élément de
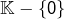 est inversible pour
est inversible pour 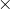
Les exemples les plus courants de corps sont :
- le corps
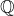 des nombres rationnels
des nombres rationnels - le corps
 des nombres réels
des nombres réels - le corps
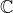 des nombres complexes
des nombres complexes
Tout corps est un anneau intègre, mais la réciproque est fausse. Par exemple ![]() est un anneau intègre, mais ses seuls éléments inversibles sont -1 et 1. Cependant, tout anneau intègre fini est un corps.
est un anneau intègre, mais ses seuls éléments inversibles sont -1 et 1. Cependant, tout anneau intègre fini est un corps.
Etant donné un entier ![]() l’anneau quotient
l’anneau quotient ![]() est un corps lorsque
est un corps lorsque ![]() est un nombre premier.
est un nombre premier.
Le cardinal d’un corps fini est de la forme ![]() où
où ![]() est premier et
est premier et ![]() Réciproquement, pour tout nombre premier
Réciproquement, pour tout nombre premier ![]() et pour tout entier
et pour tout entier ![]() il existe un corps de cardinal
il existe un corps de cardinal ![]() et deux tels corps sont isomorphes.
et deux tels corps sont isomorphes.
La caractéristique d’un corps ![]() est l’unique entier
est l’unique entier ![]() tel que
tel que ![]() soit le noyau de l’unique morphisme d’anneaux
soit le noyau de l’unique morphisme d’anneaux ![]() Cet entier est 0 ou bien un nombre premier.
Cet entier est 0 ou bien un nombre premier.
Les seuls idéaux d’un corps ![]() sont l’idéal nul et
sont l’idéal nul et ![]() Réciproquement, si les seuls idéaux d’un anneau commutatif (non nul)
Réciproquement, si les seuls idéaux d’un anneau commutatif (non nul) ![]() sont
sont ![]() et
et ![]() alors
alors ![]() est un corps.
est un corps.
Tout anneau intègre peut être plongé dans un corps, appelé son corps de fractions. Le corps des fractions de ![]() est
est ![]() Le corps des fractions de l’anneau
Le corps des fractions de l’anneau ![]() des polynômes à coefficients dans
des polynômes à coefficients dans ![]() est le corps
est le corps ![]() des fractions rationnelles.
des fractions rationnelles.
Etant donnés un corps ![]() un sous-corps
un sous-corps ![]() de
de ![]() et une partie
et une partie ![]() de
de ![]() on note
on note ![]() le sous-corps de
le sous-corps de ![]() engendré par
engendré par ![]() Par exemple :
Par exemple : ![]()
Le sous-anneau de ![]() engendré par
engendré par ![]() et
et ![]() est noté
est noté ![]() Par exemple :
Par exemple : ![]() est l’anneau des entiers de Gauss.
est l’anneau des entiers de Gauss.
CROISSANCES COMPAREES
En gros, la propriété dite des « croissances comparées » exprime la domination, à l’infini, de la fonction exponentielle sur toute fonction puissance (d’exposant fixe !).
De manière précise, il s’agit du résultat suivant :
Proposition
Pour tout ![]() :
:
![]()
Si l’on suppose connu le fait que :
(![]() )
) ![]()
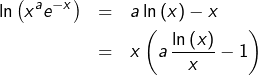
![]()
Avec un ordinateur, il convient d’être prudent lorsqu’on trace le graphe de ![]() pour un exposant
pour un exposant ![]() « assez grand » .
« assez grand » .
Par exemple, voici ce qu’on obtient pour ![]() et un tracé sur l’intervalle
et un tracé sur l’intervalle ![]() :
:
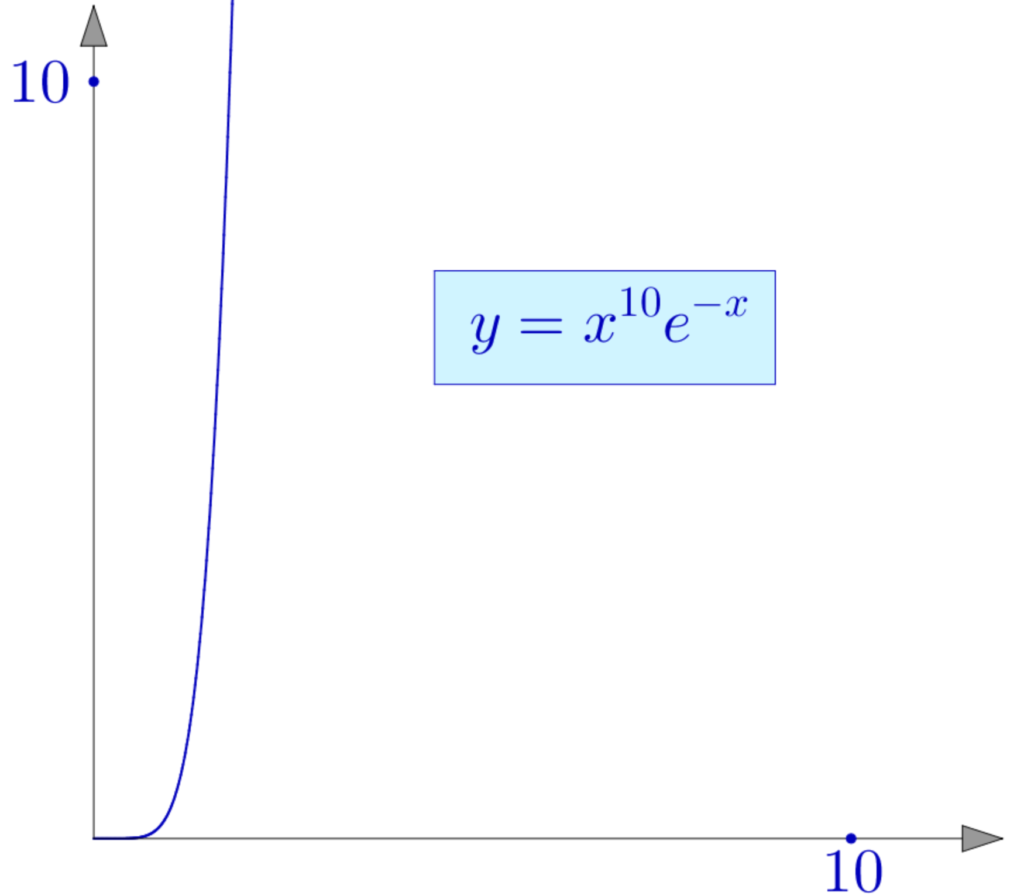
On n’a pas l’impression de voir le graphe d’une fonction qui tend vers 0 en l’infini … ce qui est pourtant le cas ! Mais voici ce que donne le tracé de la même fonction sur ![]() :
:
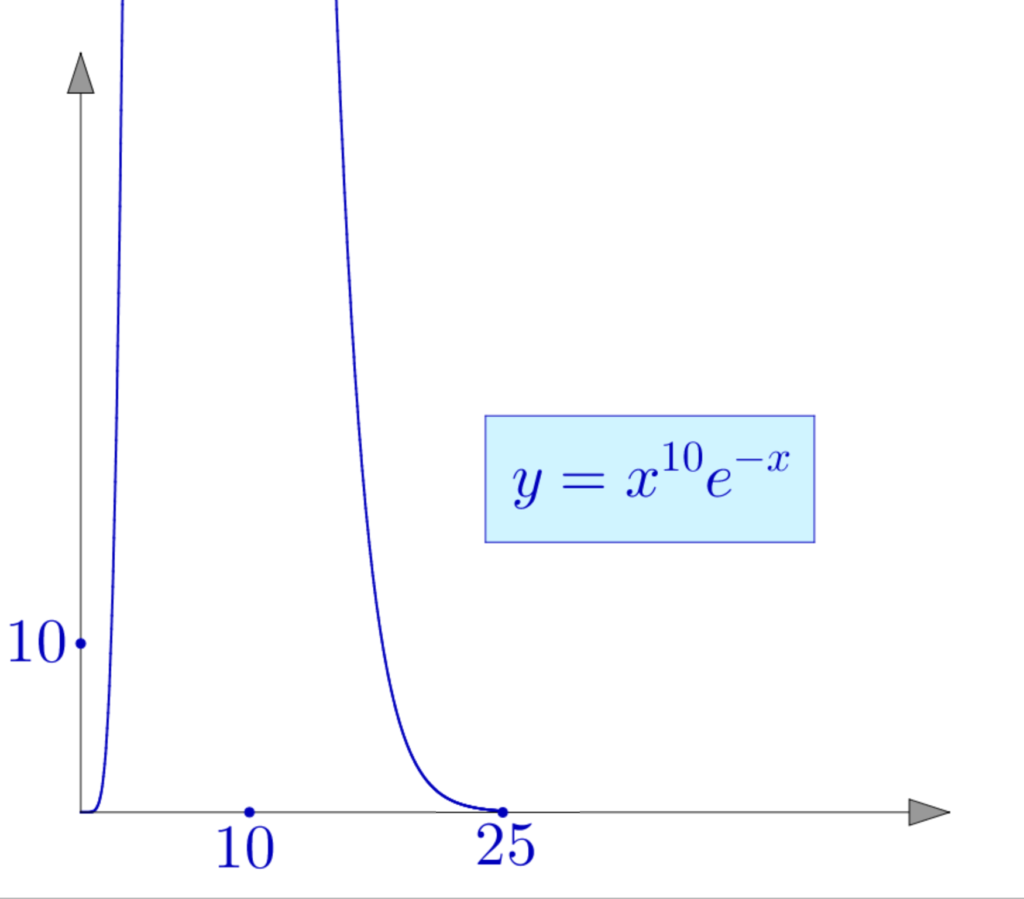
Cette fois, le dessin correspond mieux à ce qu’on attend. Et il ne faut pas s’étonner, sur ce second dessin, de ne pas voir le maximum : il ne peut pas être visible à cette échelle ! En effet la dérivée de ![]() est
est ![]() et le maximum est donc atteint pour
et le maximum est donc atteint pour ![]() Il vaut
Il vaut ![]()

