Lettre K
KRONECKER (symbole de)
Si ![]() est un ensemble quelconque et
est un ensemble quelconque et ![]() un couple d’éléments de
un couple d’éléments de ![]() , on note :
, on note :
![]()
Cette notation est d’usage fréquent, notamment en algèbre linéaire.
Exemples
Dans ce qui suit, ![]() désigne un corps (
désigne un corps (![]() ou
ou ![]() généralement).
généralement).
- Soit
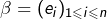 une base d’un
une base d’un 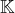 -espace vectoriel
-espace vectoriel 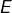 . Pour
. Pour 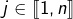 , on note
, on note 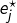 l’unique forme linéaire vérifiant :
l’unique forme linéaire vérifiant :
C’est la j-ème forme coordonnée relativement à cette base. On peut montrer que la famille![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\forall i\in\llbracket1,n\rrbracket,\,e_j^\star(e_i)=\delta_{i,j}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0f57268dd0abf2769a5567fe2f190f95_l3.png)
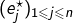 est une base de
est une base de 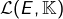 ; on l’appelle la base duale de
; on l’appelle la base duale de 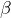 .
. - Etant donnés un entier
 et un couple
et un couple 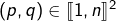 , on note
, on note 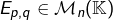 la matrice dont les termes sont tous nuls, à l’exception de celui situé à l’intersection de la ligne
la matrice dont les termes sont tous nuls, à l’exception de celui situé à l’intersection de la ligne 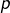 et de la colonne
et de la colonne 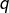 , qui vaut 1. On peut donc écrire :
, qui vaut 1. On peut donc écrire :
Les matrices![Rendered by QuickLaTeX.com \[\boxed{E_{p,q}=\left[\delta_{p,i}\delta_{q,j}\right]_{1\leqslant i,j\leqslant n}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-41efcff105f8e719920bc459fd281004_l3.png)
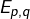 forment la base canonique de
forment la base canonique de 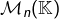 . La formule suivante est utile :
. La formule suivante est utile :![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\forall(p,q,r,s)\in\llbracket1,n\rrbracket^4,\,E_{p,q}E_{r,s}=\delta_{q,r}E_{p,s}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e022d4e045c6bfa3991a922619317918_l3.png)
- Etant donnés un entier
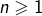 , des scalaires
, des scalaires 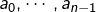 tous distincts et des scalaires
tous distincts et des scalaires 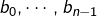 quelconques, il existe un unique polynôme
quelconques, il existe un unique polynôme ![Rendered by QuickLaTeX.com P\in\mathbb{K}_{n-1}[X]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c6ad3a6872066ac5c597f1fb5fa7761b_l3.png) tel que
tel que 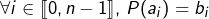 .
.
Si l’on pose, pour tout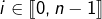 :
:
alors![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{L_i=\prod_{0\leqslant k\leqslant n-1\atop k\neq i}\frac{X-a_k}{a_i-a_k}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-54bc799c7c278e3674686d618ce22c81_l3.png)
et le polynôme![Rendered by QuickLaTeX.com \[\forall(i,j)\in\llbracket0,n-1\rrbracket^2,\,L_i(a_j)=\delta_{i,j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7c4f4087c6c77a358d9b02583f6dde4d_l3.png)
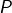 ci-dessus se décompose sous la forme :
ci-dessus se décompose sous la forme :
Pour plus d’information sur ces polynômes, on pourra se reporter à cette vidéo.![Rendered by QuickLaTeX.com \[P=\sum_{i=0}^{n-1}b_iL_i\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-961f4558df627072e00d8e97e2d63a19_l3.png)

