Exercices sur la partie entière – 01

icone-math-OS-Exos

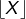On note \lfloor X\rfloor la partie entière par défaut 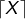du réel X et \lceil X\rceil sa partie entière par excès.

Rappelons que, par définition :

    \[\lfloor X\rfloor=\max\{k\in\mathbb{Z};\,k\leqslant x\}\]

    \[\lceil X\rceil=\min\{k\in\mathbb{Z};\,k\geqslant x\}\]

exercice 1 facile

Simplifier, pour tout n\in\mathbb{Z}, l’expression :

    \[\left\lfloor \frac{n}{2}\right\rfloor +\left\lceil \frac{n}{2}\right\rceil \]

Comparer les entiers :

    \[\left\lceil\frac{n-1}2\right\rceil\quad\text{et}\quad\left\lfloor\frac n2\right\rfloor\]

exercice 2 facile

Soient a,b,q des entiers naturels non nuls. On suppose que a\leqslant b.

Combien existe-t-il de multiples de q compris, au sens large, entre a et b ?

exercice 3 facile

On définit la “partie fractionnaire” d’un quelconque x\in\mathbb{R} par \left\langle x\right\rangle =x-\left\lfloor x\right\rfloor .

Prouver que la fonction x\mapsto\left(-1\right)^{\left\lfloor x\right\rfloor }\left\langle x\right\rangle est périodique.

Calculer, pour tout x\in\mathbb{R} :

    \[ \lim_{n\rightarrow\infty}\,\frac{1}{n^{2}}\,\sum_{k=1}^{n}\,\left\lfloor kx\right\rfloor \]

Montrer que, pour tout n\in\mathbb{N}^{\star}, l’entier \left\lfloor 2\sqrt{n^{2}+n+1}\right\rfloor est impair.

On note D l’ensemble de définition de la fonction tangente. Montrer que pour tout x\in D, il existe un entier n\in\mathbb{Z} (qu’on exprimera en fonction de x) tel que \arctan\left(\tan\left(x\right)\right)=x-n\pi.

Comparer, pour tout réel positif x, les entiers \left\lfloor \sqrt{x}\right\rfloor et \left\lfloor \sqrt{\left\lfloor x\right\rfloor }\right\rfloor .

Déterminer les applications f:\mathbb{R}\rightarrow\mathbb{R} telles que :

    \[\forall\left(x,y\right)\in\mathbb{R}^{2},\thinspace f\left(\left\lfloor x\right\rfloor y\right)=f\left(x\right)\left\lfloor f\left(y\right)\right\rfloor \]

exercice 9 difficile

Etablir la convergence de l’intégrale impropre :

    \[ E=\int_{0}^{1}\,\left(\frac{1}{t}-\left\lfloor \frac{1}{t}\right\rfloor \right)\,dt\]


et la calculer (le résultat fait intervenir une célèbre constante mathématique).

En déduire la valeur de :

    \[ \lim_{n\rightarrow\infty}\,\frac{1}{n}\,\sum_{k=1}^{n}\,\frac{n\textrm{ mod }k}{k}\]

Cliquer ici pour accéder aux indications
Cliquer ici pour accéder aux solutions

Partager cet article
  •  
  •  
  •  
  •  
Tags: , , , , , , , ,

Laisser un commentaire