

Soit ![]() Si
Si ![]() est pair alors, en posant
est pair alors, en posant ![]() :
:
![]()
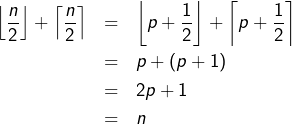
On conclut que :
![]()

Les multiples de ![]() sont les nombres de la forme
sont les nombres de la forme ![]() , avec
, avec ![]() entier.
entier.
La condition [ ![]() compris entre
compris entre ![]() et
et ![]() ] équivaut à :
] équivaut à :
![]()
ou encore à :
![]()
Il en résulte que le nombre ![]() de valeurs possibles pour
de valeurs possibles pour ![]() (et donc pour
(et donc pour ![]() est :
est :
![Rendered by QuickLaTeX.com \[\boxed{N_{a,b}=\left\lfloor \frac{b}{q}\right\rfloor -\left\lceil \frac{a}{q}\right\rceil +1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aba6c9d8b87b04c86ee7293178ba2805_l3.png)
Exemple
Le nombre de multiples de 7 compris (au sens large) entre ![]() et
et ![]() est :
est :
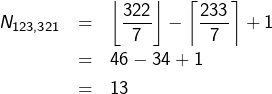
Ces entiers sont ceux de la forme ![]() pour
pour ![]() à savoir :
à savoir :
238, 245, 252, 259, 266, 273, 280, 287, 294, 301, 308, 315, 322.

On commence par observer que, pour tout ![]() :
:
![]()
Pour une preuve de ceci, voir ce passage de la vidéo fiche technique : la fonction partie entière.
Il en résulte que la fonction partie fractionnaire est 1-périodique. En effet, pour tout ![]() :
:
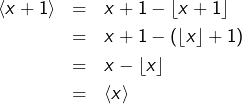
Par conséquent, si l’on pose ![]() alors :
alors :
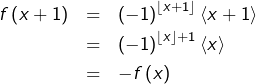
On a prouvé que ![]() est 2-périodique.
est 2-périodique.
Etant donné ![]() posons pour tout
posons pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ u_{n}=\frac{1}{n^{2}}\,\sum_{k=1}^{n}\,\left\lfloor kx\right\rfloor \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-00049ccd9a22c739f100d0edce0650dd_l3.png)
Il suffit d’encadrer :
![]()
![Rendered by QuickLaTeX.com \[ \frac{1}{n^{2}}\sum_{k=1}^{n}\,\left(kx-1\right)\leqslant u_{n}<\frac{1}{n^{2}}\sum_{k=1}^{n}\,kx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-54a1dd6f34c8056a0c0628fa49df4c0d_l3.png)
![]()
Avec le théorème d’encadrement (alias théorème des gendarmes) , on conclut que :
![]()

On observe que, pour tout ![]() :
:
![]()
![]()
Par stricte croissance de la racine carrée, il en résulte que :
![]()
![]()
Finalement, l’entier ![]() est impair.
est impair.

Rappelons tout d’abord que l’ensemble de définition de la fonction tangente est :
![]()
![]()
Soit ![]() et soit
et soit ![]() l’unique entier vérifiant :
l’unique entier vérifiant :
![]()
Cet encadrement équivaut à :
![]()
![]()
Par ailleurs, les applications :
![]()
![]()
![]()
Il reste à mettre tout ceci bout à bout. Pour ![]() on notant
on notant ![]() l’entier défini par
l’entier défini par ![]() :
:
![]()
Finalement :
![Rendered by QuickLaTeX.com \[\boxed{\forall x\in D,\thinspace\arctan\left(\tan\left(x\right)\right)=x-\left\lfloor \frac{x}{\pi}+\frac{1}{2}\right\rfloor \pi}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2bedcd2483775da6151df8e39537c995_l3.png)

Soit ![]() un réel positif ou nul.
un réel positif ou nul.
- Vu que
 la croissance de
la croissance de 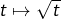 donne
donne  Puis, comme
Puis, comme 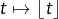 est aussi croissante :
est aussi croissante : 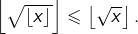
- Comme
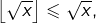 alors
alors 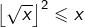 puis comme
puis comme 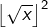 est un entier, on voit que
est un entier, on voit que 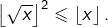 Ainsi
Ainsi 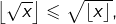 et comme
et comme 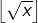 est un entier, alors
est un entier, alors 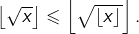
De tout cela, on conclut que :
![]()

Soit ![]() telle que :
telle que :
![]()
▷ Supposons que ![]() soit à valeurs dans
soit à valeurs dans ![]() Alors
Alors ![]() En particulier pour
En particulier pour ![]() et donc
et donc ![]() est l’application nulle.
est l’application nulle.
▷ Supposons maintenant ![]() et fixons un tel
et fixons un tel ![]() . Comme
. Comme ![]() :
:
![]()
![]()
En particulier ![]() :
:
![]()
Donc ![]()
- Si
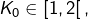 alors
alors 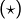 donne
donne 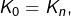 donc
donc  est constante et cette constante appartient à
est constante et cette constante appartient à 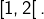
- Et si
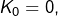 alors en prenant
alors en prenant 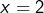 et
et 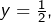 il vient
il vient 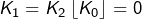 puis en prenant
puis en prenant  et
et 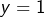 il vient
il vient 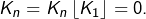 Dans ce cas,
Dans ce cas, 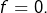
Réciproquement, les fonctions constantes
![]()

Considérons l’application
![]()
Ses restrictions aux segements de la forme ![]() avec
avec ![]() sont continues par morceaux.
sont continues par morceaux.
Il s’agit de montrer que l’intégrale partielle ![]() admet une limite finie lorsque
admet une limite finie lorsque ![]() tend vers
tend vers ![]() par valeurs supérieures, et de calculer cette limite.
par valeurs supérieures, et de calculer cette limite.
Posons, dans un premier temps :
![]()
Alors :
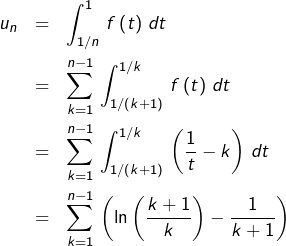
donc, après sommation télescopique et ré-indexation :
![Rendered by QuickLaTeX.com \[ u_{n}=\ln\left(n\right)-\sum_{k=2}^{n}\,\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ed51963edd24eefd197cf07c69ca93df_l3.png)
![]()
Revenons à présent à l’intégrale partielle. Pour tout ![]() posons
posons ![]()
Comme ![]() est majorée par 1 :
est majorée par 1 :
![]()
![]()
En définitive, l’intégrale proposée converge et
![Rendered by QuickLaTeX.com \[ \boxed{\int_{0}^{1}\,\left(\frac{1}{t}-\left\lfloor \frac{1}{t}\right\rfloor \right)\,dt=1-\gamma}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-70895a310b51ba3c31dd4f0dd910252b_l3.png)
Comme ![]() il vient :
il vient :
![Rendered by QuickLaTeX.com \[ \frac{1}{n}\,\sum_{k=1}^{n}\,\frac{n\textrm{ mod }k}{k}=\frac{1}{n}\,\sum_{k=1}^{n}\,\left(\frac{n}{k}-\left\lfloor \frac{n}{k}\right\rfloor \right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3ea7c355e699ff906908e56afa97b9c5_l3.png)
On reconnaît une somme de Riemann attachée à l’intégrale précédente.
D’après le théorème de convergence des sommes de Riemann pour les intégrales impropres (voir l’exercice n° 8 de cette fiche) :
![Rendered by QuickLaTeX.com \[ \boxed{\lim_{n\rightarrow\infty}\,\frac{1}{n}\,\sum_{k=1}^{n}\,\frac{n\textrm{ mod }k}{k}=1-\gamma}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-70ce35a31591be2fa48ede5a33f0f3fc_l3.png)
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
