
1 – « Factoriser » … De quoi s’agit-il ?
Une fonction polynôme (ou, pour faire court, un polynôme) est une fonction P que l’on peut définir, pour tout ![]() par une formule du type :
par une formule du type :
(![]() )
) ![]()
Si ![]() , on dit que
, on dit que ![]() est de degré
est de degré ![]()
Par exemple, en choisissant ![]() ainsi que
ainsi que ![]()
![]()
![]()
![]() et
et ![]() , on obtient, pour tout
, on obtient, pour tout ![]() :
:
![]()
L’égalité ![]() fournit l’expression développée d’un polynôme
fournit l’expression développée d’un polynôme ![]() Mais un polynôme peut parfois se présenter sous un autre jour …
Mais un polynôme peut parfois se présenter sous un autre jour …
Considérons la fonction ![]() définie pour tout
définie pour tout ![]() par :
par :
(![]() )
) ![]()
![]() est un polynôme puisque, pour tout
est un polynôme puisque, pour tout ![]() :
:
(![]() )
) ![]()
Le passage de ![]() à
à ![]() se fait mécaniquement et ne soulève aucune difficulté (on transforme le produit en somme en utilisant la distributivité de la multiplication sur l’addition).
se fait mécaniquement et ne soulève aucune difficulté (on transforme le produit en somme en utilisant la distributivité de la multiplication sur l’addition).
Mais aurions-nous été capables, en partant de ![]() de retrouver
de retrouver ![]() ?
?
C’est le problème de la factorisation.
L’intérêt de factoriser un polynôme résulte principalement de deux propriétés de la multiplication des nombres réels :
- Propriété 1 (« intégrité ») : si
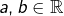 sont tels que
sont tels que 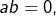 alors
alors 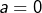 ou
ou 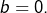
- Propriété 2 (« règle des signes ») : si
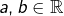 sont de même signe (tous deux positifs ou nuls, ou bien tous deux négatifs ou nuls), alors
sont de même signe (tous deux positifs ou nuls, ou bien tous deux négatifs ou nuls), alors 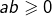 et, s’ils sont de signes contraires, alors
et, s’ils sont de signes contraires, alors 
→ La propriété 1 est utile pour déterminer les racines éventuelles d’un polynôme : on résout l’équation ![]() en cherchant à factoriser
en cherchant à factoriser ![]() .
.
Précisons que ![]() est une racine de
est une racine de ![]() lorsque
lorsque ![]() .
.
→ La propriété 2 permet l’étude du signe d’un polynôme, dès lors qu’on a obtenu une factorisation de celui-ci. Ceci s’avère notamment utile lorsqu’on étudie les variations d’une fonction polynôme : on doit déterminer le signe de sa dérivée (laquelle dérivée est, elle aussi polynomiale !). Ajoutons que cette remarque s’étend plus généralement à l’étude des variations d’une fraction de polynômes et, au-delà, au cas de fonctions dont le signe de la dérivée est contrôlé par un polynôme. Par exemple, une fonction de la forme ![]() où
où ![]() sont des polynômes.
sont des polynômes.
2 – Les outils de base
Factoriser un polynôme consiste donc à l’écrire (si possible) comme un produit …
… mais de façon « non triviale » !
Clairement, le fait d’écrire ![]() n’intéresse pas grand monde…
n’intéresse pas grand monde…
Trois outils simples sont disponibles pour factoriser des polynômes. Les voici :
Règle 1
La propriété de distributivité, déjà invoquée plus haut avec le polynôme Q, dit que si ![]() sont trois nombres réels quelconques, alors
sont trois nombres réels quelconques, alors ![]() En lisant cette égalité de droite à gauche, on dit qu’ « on met
En lisant cette égalité de droite à gauche, on dit qu’ « on met ![]() en facteur dans l’expression
en facteur dans l’expression ![]() ».
».
Règle 2
Ensuite, viennent les identités remarquables « standard » :
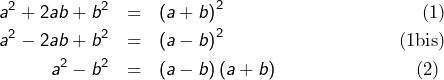
Règle 3
Enfin, si ![]() est un polynôme et si
est un polynôme et si ![]() est une racine de
est une racine de ![]() alors il existe un polynôme
alors il existe un polynôme ![]() tel que, pour tout
tel que, pour tout ![]() :
:
![]()
Voyons quelques exemples d’utilisation de ces règles …
Exemple 1
Pour factoriser ![]() on applique d’abord la distributivité, ce qui donne :
on applique d’abord la distributivité, ce qui donne :
![]()
![]()
Exemple 2
Pour factoriser ![]() on effectue une mise sous forme canonique (technique à la base de la résolution des équations du second degré), ce qui consiste à modifier l’écriture de
on effectue une mise sous forme canonique (technique à la base de la résolution des équations du second degré), ce qui consiste à modifier l’écriture de ![]() pour faire apparaître une différence de deux carrés :
pour faire apparaître une différence de deux carrés :
![]()
![]()
Exemple 3
Pour factoriser ![]() on observe que
on observe que ![]() Il est donc possible de mettre
Il est donc possible de mettre ![]() en facteur :
en facteur :
![]()
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{cccc}a & = & 1 & (\text{coefft de }x^{3})\\\\b-a & = & 0 & (\text{coefft de }x^{2})\\\\c-b & = & -2 & (\text{coefft de }x)\\\\-c & = & 1 & (\text{coefft constant)}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5930fa4b63ee678e5264319227923178_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[x^{2}+x-1=\left(x+\frac{1}{2}\right)^{2}-\frac{5}{4}=\left(x+\frac{1}{2}-\frac{\sqrt{5}}{2}\right)\left(x+\frac{1}{2}+\frac{\sqrt{5}}{2}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-455039a6a33ccbb36f15476eadb57b23_l3.png)
En conclusion :
![]()
Exemple 4
Pour factoriser ![]() on peut commencer avec l’identité remarquable (2) :
on peut commencer avec l’identité remarquable (2) :
![]()
On peut observer que ![]() et
et ![]() ce qui permet de factoriser
ce qui permet de factoriser ![]() par
par ![]() et
et ![]() par
par ![]() Les détails sont laissés au lecteur 🙂
Les détails sont laissés au lecteur 🙂
On trouve au final :
![]()
Cette dernière affirmation se justifie par le fait que, pour tout ![]() :
:
![]()
3 – D’autres identités remarquables
Dans l’exemple 4 ci-dessus, nous avons factorisé ![]() sous la forme :
sous la forme :
![]()
Nous aurions pu invoquer l’identité remarquable suivante, valable pour tous réels ![]() :
:
(![]() )
) ![]()
![]()
On peut pousser le curseur un cran plus loin, avec la généralisation suivante de l’identité ![]() qui donne une factorisation pour la différence de deux puissances
qui donne une factorisation pour la différence de deux puissances ![]() èmes (l’entier
èmes (l’entier ![]() est supérieur ou égal à
est supérieur ou égal à ![]() ) :
) :
(![]() )
) ![]()
La somme qui apparaît en facteur de ![]() est composée de
est composée de ![]() termes : le premier est
termes : le premier est ![]() et les suivants sont obtenus en réduisant progressivement l’exposant de
et les suivants sont obtenus en réduisant progressivement l’exposant de ![]() tandis que l’exposant de b est progressivement augmenté. Par exemple, pour
tandis que l’exposant de b est progressivement augmenté. Par exemple, pour ![]() :
:
![]()
![]()
Si vous avez l’habitude à la notation ![]() , vous comprendrez que la formule
, vous comprendrez que la formule ![]() s’écrive ainsi :
s’écrive ainsi :
![Rendered by QuickLaTeX.com \[a^{n}-b^{n}=\left(a-b\right)\sum_{k=1}^{n}a^{k-1}b^{n-k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2d49388f7ad14066f4f0bade02b24ab3_l3.png)
4 – Factoriser en utilisant le « test des racines rationnelles »
Dans l’exemple 3, nous avons « observé » que ![]() On peut raisonnablement considérer que ça saute au yeux … Et puis, lorsqu’on cherche à factoriser un polynôme à coefficients entiers, la première chose qu’on fait généralement consiste à l’évaluer en 1 ou en -1 et peut-être aussi en d’autres petits entiers, en espérant mettre la main sur une racine et commencer ainsi le processus de factorisation.
On peut raisonnablement considérer que ça saute au yeux … Et puis, lorsqu’on cherche à factoriser un polynôme à coefficients entiers, la première chose qu’on fait généralement consiste à l’évaluer en 1 ou en -1 et peut-être aussi en d’autres petits entiers, en espérant mettre la main sur une racine et commencer ainsi le processus de factorisation.
Considérons maintenant le cas de
![]()
![]()
Point de racine en vue 🙁
Peut-être ce polynôme ne possède-t-il aucune racine réelle ? Ou alors seulement des racines irrationnelles ?
Peut-être existe-t-il des racines rationnelles (mais bien cachées) ? Et si oui, comment les trouver ?
C’est là qu’intervient le « test des racines rationnelles », dont voici l’énoncé :
Test des racines rationnelles
Soit ![]() un polynôme défini par :
un polynôme défini par :
![]()
Si
(![]() )
) ![]()
Nous n’allons pas démontrer ce résultat ici (sa preuve se trouve dans tous les cours standards d’arithmétique; elle repose pour l’essentiel sur le théorème de Gauss, qui affirme que si un entier ![]() divise le produit
divise le produit ![]() de deux entiers et si
de deux entiers et si ![]() et
et ![]() sont premiers entre eux, alors
sont premiers entre eux, alors ![]() divise
divise ![]() ).
).
En revanche, nous allons nous en servir pour déterminer les éventuelles racines rationnelles de
![]()
La condition nécessaire ![]() s’écrit :
s’écrit :
![]()
![]()
Les éventuelles racines rationnelles de ![]() figurent donc parmi les nombres suivants :
figurent donc parmi les nombres suivants :
![]()
Muni d’une calculette ou d’un ordinateur, on peut rapidement tester chacune de ces huit valeurs … et constater que la seule racine rationnelle de ![]() est
est ![]()
Et on ne peut pas, raisonnablement, qualifier cette racine d’évidente !
Et maintenant ? La [Règle 3] permet de factoriser par ![]() ou, ce qui revient au même, par
ou, ce qui revient au même, par ![]() Il existe ainsi un polynôme
Il existe ainsi un polynôme ![]() de degré
de degré ![]() tel que, pour tout
tel que, pour tout ![]() :
:
![]()
![]()
J’espère que ce rapide survol vous aura plu 🙂
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
