On considère une liste comportant les entiers de 1 à 8 exactement, mais dans un ordre arbitraire.

On se donne le droit d’effectuer, autant de fois qu’on veut, l’une ou l’autre des opérations suivantes :

➮ opération T : le troisième chiffre de la liste est déplacé en tête de celle-ci

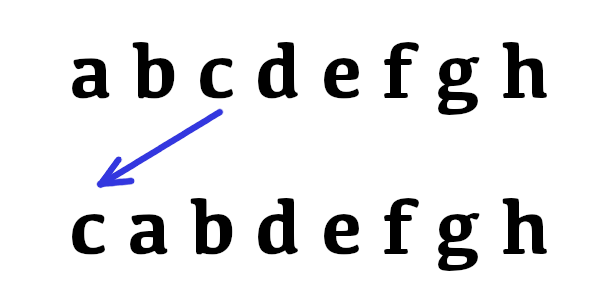
➮ opération H : le huitième chiffre de la liste est déplacé en tête de celle-ci

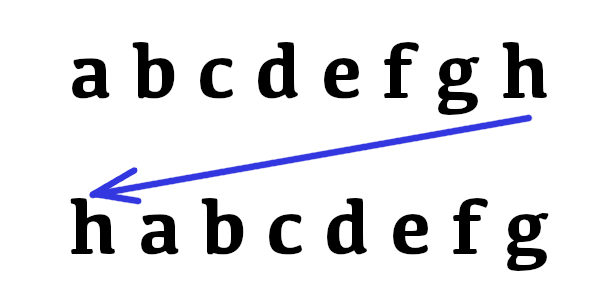
Par exemple, à partir de :

52183647

on obtient, en effectuant successivement T, puis H :

15283647

71528364

Sauriez-vous prouver que, quelle que soit la liste initiale, il est possible d’atteindre 12345678 en effectuant les opérations T et H un nombre convenable de fois et dans un ordre approprié ?

Une solution est disponible ici