icone-challenge-math-OS

Solution pour le challenge 45

Ce challenge est lié à un aspect élémentaire de la théorie des groupes.

Les opérations T et H peuvent, en effet, être vues comme des éléments du groupe symétrique \displaystyle{\mathfrak{S}_{8}} et tout revient à expliquer qu’elles engendrent, à elles seules, le groupe entier.

En partant d’une permutation quelconque abcdefgh des chiffres 1 à 8 et en effectuant (dans cet ordre) :

H H T H H T H H T H

on obtient bacdefgh. On a simplement échangé les deux premiers chiffres, comme le montre la petite vidéo ci-dessous :

Notons S cette permutation : \boxed{S=\left(1,2\right)} (c’est une transposition).

En partant toujours de abcdefgh et en appliquant H sept fois de suite, on obtient bcdefgha, ce qui revient à appliquer la permutation inverse de H (et c’est logique vu que : H^{8}=id).

Notons C cette permutation : \boxed{C=\left(1,2,3,4,5,6,7,8\right)} (c’est un cycle de longueur 8).

Voici maintenant l’argument-clef : \left\{S,C\right\} est une partie génératrice du groupe \mathfrak{S}_{8} (ce point est un cas particulier d’un résultat détaillé en annexe). Autrement dit, toutes les permutations (il y en a au total 8!=40\thinspace320) s’obtiennent en composant entre elles S et C et donc, in fine, en composant entre elles H et T, ce qui règle la question.

Annexe – une partie génératrice de \mathfrak{S}_n

Etant donné un entier n\geqslant2 notons S et C deux éléments particuliers du groupe \mathfrak{S}_{n} :

➡ S désigne la transposition \left(1,2\right) : les entiers 1 et 2 sont échangés; tous les autres sont fixes.

➡ C désigne le cycle \left(1,2,\cdots,n\right) :

  • pour tout i\in\left\llbracket 1,n-1\right\rrbracket , l’image de i est i+1
  • l’image de n est 1

Notons \mathcal{G} le sous-groupe de \mathfrak{S}_{n} engendré par \left\{S,C\right\} et prouvons deux lemmes :

[Lemme 1] pour tout i\in\left\llbracket 1,n-1\right\rrbracket, la transposition \left(i,i+1\right) appartient à \mathcal{G}

[Lemme 2] toute transposition est produit de transpositions du type (i,i+1)

Il en résultera que \mathcal{G} contient toutes les transpositions.

Or, il est classique que celles-ci engendrent \mathfrak{S}_{n}, d’où la conclusion :

    \[\boxed{\mathcal{G}=\mathfrak{S}_{n}}\]

Le cas particulier n = 8 permet de traiter le challenge.

Voici le détail pour chacun des deux lemmes :

Preuve du lemme 1

Montrons que, pour tout i\in\left\llbracket 1,n-1\right\rrbracket :
\boxed{C^{i-1}\circ S\circ S^{-\left(i-1\right)}=\left(i,i+1\right)}

➡ l’égalité est évidente pour i=1

➡ En la supposant vraie pour un certain i\in\left\llbracket 1,n-2\right\rrbracket :

    \begin{eqnarray*}& &C^{i}\circ S\circ C^{-i}\\& = & C\circ C^{i-1}\circ S\circ C^{-\left(i-1\right)}\circ C\\& = & C\circ\left(i,i+1\right)\circ C^{-1}\\& = & \left(i+1,i+2\right)\end{eqnarray*}

Le résultat annoncé est ainsi établi par récurrence.

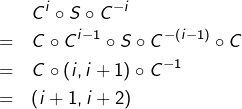
Preuve du lemme 2

Pour tout k\in\llbracket2,n\rrbracket, notons t_k la transposition (k-1,k), qui échange k-1 et k.

Etant donnés i,j\in\left\llbracket 1,n\right\rrbracket tels que i<j, on constate que :
\boxed{\left(i,j\right)=t_j\circ\cdots\circ t_{i+2}\circ t_{i+1}\circ t_{i+2}\circ\cdots\circ t_j}

Par exemple (dans \mathfrak{S}_n pour n\geqslant 5) :
\left(1,5\right)=\left(4,5\right)\circ\left(3,4\right)\circ\left(2,3\right)\circ\left(1,2\right)\circ\left(2,3\right)\circ\left(3,4\right)\circ\left(4,5\right)

Une solution voisine de celle publiée ci-dessus a été obtenue par Alexandre Boyer, étudiant en section MP* au lycée Thiers (Marseille).

Pour consulter l’énoncé, c’est ici

Partager cet article
    

Laisser un commentaire