Etant donnée une suite ![]() de réels positifs, on note pour tout
de réels positifs, on note pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[S_n=\sum_{k=1}^nu_k\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7e75a4212ac2f1e9c024884f5c2a963c_l3.png)
On demande ici de statuer dans le cas particulier où, pour tout ![]() :
:
![]()
Plusieurs méthodes peuvent être envisagées …
Une solution est disponible ici
Partager cet article
Etant donnée une suite ![]() de réels positifs, on note pour tout
de réels positifs, on note pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[S_n=\sum_{k=1}^nu_k\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7e75a4212ac2f1e9c024884f5c2a963c_l3.png)
On demande ici de statuer dans le cas particulier où, pour tout ![]() :
:
![]()
Plusieurs méthodes peuvent être envisagées …
Une solution est disponible ici
Voici une idée de démonstration qui me semble juste :
(1)on peut montrer que sin(n) est dense dans [-1;1] donc a fortiori |sin(n)| est dense dans [0;1](la marge n’est pas assez grande pour en contenir la démonstration)
(2)soit A ={n appartenant N ; |sin(n)| >0,5}
(3) d’après 1 card(A) = infini
(4) donc série(pour n appartenant à N)(|sin(n)|) > série(pour n appartenant à A)(sin(|n|) > card(A)*0.5 > infini
Qu’on m’excuse pour cette démonstration très peu rigoureuse j’ai ici seulement mis une idée qui me semble bonne
Cela demanderait à être mis en forme, mais c’est une idée tout à fait valable ! Cela dit, on peut faire quelque chose de nettement plus élémentaire (ce qui ne veut pas dire plus facile) en évitant la densité de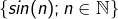 dans
dans ![Rendered by QuickLaTeX.com [-1,1].](https://math-os.com/wp-content/ql-cache/quicklatex.com-20b23c4fdfe10c70017a32af684ca806_l3.png)
En tous cas, merci et bravo pour votre participation 😉