Solution pour le challenge 16
Méthode 1
Commençons par calculer, pour tout réel 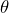 non multiple de
non multiple de 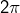 , la somme :
, la somme :
![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=1}^{n}\cos\left(k\theta\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-01ec528051d5c126ac4f636db3f5cbdf_l3.png)
Il s’agit de la partie réelle de :
![Rendered by QuickLaTeX.com \[G_{n}=\sum_{k=1}^{n}e^{ik\theta}=\sum_{k=1}^{n}\left(e^{i\theta}\right)^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7c7dfa6a105f5c6bf5e8fe323d77f7c0_l3.png)
On reconnaît une somme géométrique de raison différente de 1, puisque :
![Rendered by QuickLaTeX.com \[$e^{i\theta}=1\Leftrightarrow\exists q\in\mathbb{Z};\thinspace\theta=2q\pi\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5a8faffbb4a744536287d23ec5a78ed7_l3.png)
Par conséquent :
![Rendered by QuickLaTeX.com \[G_{n}=\frac{e^{i\theta}\left(1-e^{in\theta}\right)}{1-e^{i\theta}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3e48bab4c1456afb6be1e860b2eb1690_l3.png)
et la suite
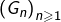
est donc bornée :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N^{\star}},\:\left|G_{n}\right|\leqslant\frac{2}{\left|1-e^{i\theta}\right|}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2f90f0bd590f9a3e2a663219d67fbe26_l3.png)
Il en résulte que la suite
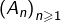
est aussi bornée, puisque pour tout
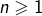
:
![Rendered by QuickLaTeX.com \[\left|A_{n}\right|=\left|\text{Re}\left(G_{n}\right)\right|\leqslant\left|G_{n}\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-faddd9a47311b7f2109fc2e3614ca6f8_l3.png)
Passons maintenant à :
![Rendered by QuickLaTeX.com \[V_{n}=\sum_{k=1}^{n}\left|\sin\left(k\right)\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4be6eac282b99e1385ef10bbc1f84b42_l3.png)
Tout réel appartenant à
![Rendered by QuickLaTeX.com \left[0,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-beb10f64e7f6b1b271629e3a8291d2e5_l3.png)
est minoré par son carré. On voit ainsi que, pour tout
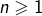
:
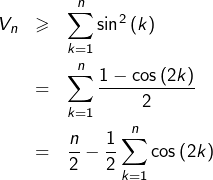
Comme la suite de terme général
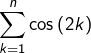
est bornée (prendre
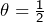
dans ce qui précède), on conclut que :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow\infty}V_{n}=+\infty}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d3b83ad6d5fc627807a4dd3664bc6e90_l3.png)
Méthode 2
Cette méthode est plus « géométrique » que la précédente.
Pour tout entier  notons
notons 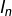 l’intervalle
l’intervalle ![Rendered by QuickLaTeX.com \left[n\pi+\frac{\pi}{3},n\pi+\frac{2\pi}{3}\right].](https://math-os.com/wp-content/ql-cache/quicklatex.com-e39d4bddaeb630130f9ee17aa44d8e90_l3.png)
D’une part, pour tout 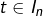 :
:
![Rendered by QuickLaTeX.com \[\left|\sin\left(t\right)\right|\geqslant\frac{\sqrt{3}}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d78743dcdf16abaeb6502b356a435f83_l3.png)
et d’autre part,
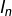
est de longueur
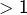
dont contient au moins un entier (et probablement un seul pour une majorité d’indices
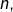
mais là n’est pas la question). Notons
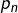
le plus petit :
![Rendered by QuickLaTeX.com \[p_{n}=\left\lceil \frac{\left(3n+1\right)\pi}{3}\right\rceil\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-171015c2b493b774506501e26ec56d79_l3.png)
On constate que :
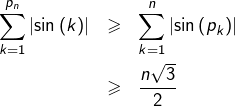
ce qui prouve que :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}V_{p_{n}}=+\infty\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-03720c63a0cba5eb85579864a258db5a_l3.png)
La suite
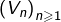
est croissante et possède une suite extraite qui diverge vers
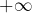
. Elle diverge donc, elle aussi, vers
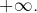
Pour consulter l’énoncé, c’est ici
![]() non multiple de
non multiple de ![]() , la somme :
, la somme :![Rendered by QuickLaTeX.com \[A_{n}=\sum_{k=1}^{n}\cos\left(k\theta\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-01ec528051d5c126ac4f636db3f5cbdf_l3.png)
![Rendered by QuickLaTeX.com \[G_{n}=\sum_{k=1}^{n}e^{ik\theta}=\sum_{k=1}^{n}\left(e^{i\theta}\right)^{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7c7dfa6a105f5c6bf5e8fe323d77f7c0_l3.png)
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[V_{n}=\sum_{k=1}^{n}\left|\sin\left(k\right)\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4be6eac282b99e1385ef10bbc1f84b42_l3.png)
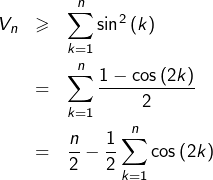
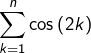 est bornée (prendre
est bornée (prendre ![]()
![]() notons
notons ![]() l’intervalle
l’intervalle ![]()
![]() :
:![]()
![]()
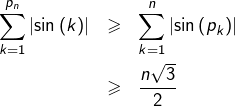
![]()

