
Cet article s’adresse à celles et ceux qui s’intéressent aux questions d’algèbre linéaire et donc – entre autres – aux étudiants des deux premières années d’enseignement supérieur scientifique.
Dans un cours d’algèbre linéaire, on aborde notamment la question des espaces vectoriels de dimension finie. On y explique que si ![]() est un corps (le plus souvent un sous-corps de
est un corps (le plus souvent un sous-corps de ![]() et si
et si ![]() est un
est un ![]() espace vectoriel possédant une famille finie et génératrice de
espace vectoriel possédant une famille finie et génératrice de ![]() , alors on peut trouver une telle famille qui soit de plus libre, et qui constitue donc une base de
, alors on peut trouver une telle famille qui soit de plus libre, et qui constitue donc une base de ![]()
En outre, toutes les bases de ![]() sont composées d’un même nombre de vecteurs. Cet entier est appelé la dimension de
sont composées d’un même nombre de vecteurs. Cet entier est appelé la dimension de ![]() et noté
et noté ![]()
Cette construction théorique n’est pas traitée ici, mais vous pouvez en découvrir tous les détails en visionnant cette vidéo et les suivantes.
Ce texte essaie de rassembler les principales méthodes qui permettent, en pratique, de calculer la dimension d’un espace vectoriel. Chacune de ces méthodes est illustrée d’exemples. Bonne lecture 🙂
1 – Intuitivement, la dimension … c’est quoi ?
De façon naïve, la dimension d’un espace vectoriel est le « nombre de degrés de liberté » dont on dispose pour s’y déplacer.
Si l’espace en question est une droite, on repère la position d’un point par son abscisse, après avoir choisi une origine et un vecteur unité. S’il s’agit d’un plan, deux nombres sont nécessaires : une abscisse et une ordonnée.
Dans l’espace usuel, on peut repérer la position d’un point par trois nombres : une abscisse X, une ordonnée Y et une côte Z.
Illustration dynamique 1
Modifier la position de l’observateur en pressant SHIFT →↑↓←.
Zoomer / dézoomer en utilisant les touches P / M.
Les sliders contrôlent les coordonnées cartésiennes du centre de la petite sphère.
Mais ce n’est pas la seule façon de s’y prendre. Par exemple, la position d’un point au voisinage de la terre peut être repérée par une latitude, une longitude et une altitude : là encore, trois nombres.
Illustration dynamique 2
Modifier la position de l’observateur en pressant SHIFT →↑↓←.
Zoomer / dézoomer en utilisant les touches P / M.
Les sliders contrôlent les coordonnées sphériques du centre de la petite sphère.
D’ailleurs, ce concept s’étend bien au-delà des espaces vectoriels (ou affines). Une sphère, par exemple, doit être considérée comme un espace de dimension 2 : par temps calme, la surface d’un océan ressemble (comme deux gouttes d’eau … il fallait oser) à un plan; tout au moins à une échelle appropriée.
Ces images mentales peuvent aider à se faire une idée intuitive de la notion de dimension.
Revenons maintenant au cadre formel des espaces vectoriels.
2 – Compter les vecteurs d’une base
Règle A
Soient ![]() un
un ![]() espace vectoriel et
espace vectoriel et ![]() .
.
Si ![]() est une base de
est une base de ![]() alors
alors ![]()
Ceci provient simplement de la définition de ![]() mentionnée dans introduction.
mentionnée dans introduction.
Voici quelques exemples d’utilisation de cette règle.
Exemple A-1
Pour tout ![]() :
:
![]()
En effet, on voit aisément (cf. détail ci-dessous) qu’en notant pour tout
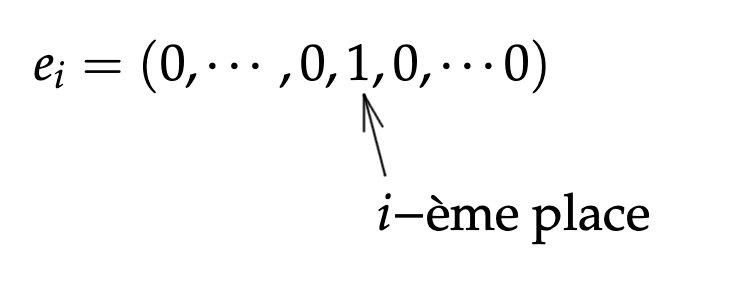
la famille ![]() est une base de
est une base de ![]() (officiellement appelée la base canonique de
(officiellement appelée la base canonique de ![]()
– Détail –
Choisissons ![]() C’est suffisant pour comprendre. Tout vecteur de
C’est suffisant pour comprendre. Tout vecteur de ![]() s’écrit sous la forme :
s’écrit sous la forme :
![]()
ce qui prouve que la famille :
![]()
Elle est de plus libre; en effet, si ![]() sont trois scalaires tels que :
sont trois scalaires tels que :
![]()
Finalement, ![]() est une base de
est une base de ![]() La généralisation à
La généralisation à ![]() quelconque est immédiate.
quelconque est immédiate.
Exemple A-2
Considérons deux réels ![]() ainsi que l’ensemble :
ainsi que l’ensemble :
![]()
Les vecteurs de ![]() sont les triplets de la forme :
sont les triplets de la forme :
![]()
![]()
![Rendered by QuickLaTeX.com \[H=\left\{ \left(x_{1},\cdots,x_{n}\right)\in\mathbb{K}^{n};\thinspace\sum_{k=1}^{n}\lambda_{k}x_{k}=0\right\}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-981204ca2bdcba76c729b939db4187f3_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\mathbb{K}^{n}\rightarrow\mathbb{K},\thinspace\left(x_{1},\cdots,x_{n}\right)\mapsto\sum_{k=1}^{n}\lambda_{k}x_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c7877d9742efeb32c9333523d9c86d2e_l3.png)
Exemple A-3
Etant donnés deux entiers ![]() l’ensemble
l’ensemble ![]() des matrices rectangulaires à
des matrices rectangulaires à ![]() lignes et
lignes et ![]() colonnes et à termes dans
colonnes et à termes dans ![]() est un
est un ![]() espace vectoriel.
espace vectoriel.
Notons ![]() la matrice de format
la matrice de format ![]() dont les termes sont tous nuls, à l’exception de celui situé à l’intersection de la ligne
dont les termes sont tous nuls, à l’exception de celui situé à l’intersection de la ligne ![]() et de la colonne
et de la colonne ![]() qui vaut 1.
qui vaut 1.
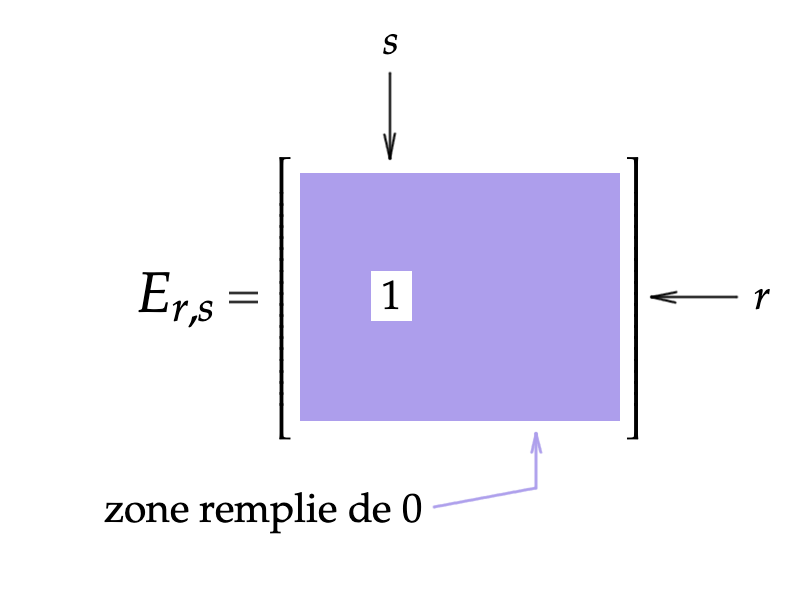
Il est facile de voir que la famille ![]() (ordonnée par exemple selon l’ordre lexicographique sur les couples d’indices) est une base de
(ordonnée par exemple selon l’ordre lexicographique sur les couples d’indices) est une base de ![]() (c’est la base canonique). En conséquence :
(c’est la base canonique). En conséquence :
![]()
Cet exemple raconte donc essentiellement la même histoire que l’exemple A-1.
Exemple A-4
Soit ![]() Dans l’espace
Dans l’espace ![]() des suites à termes dans
des suites à termes dans ![]() considérons le sous-espace
considérons le sous-espace ![]() des suites
des suites ![]() telles que :
telles que :
![]()
Posons, pour tout ![]() :
:
![]()
![]()
En d’autres termes, ![]() est la suite de scalaires dont tous les termes sont nuls, à l’exception du
est la suite de scalaires dont tous les termes sont nuls, à l’exception du ![]() ème qui vaut 1.
ème qui vaut 1.
La famille ![]() est alors une base de
est alors une base de ![]() et, de ce fait :
et, de ce fait :
![]()
3 – Dimension d’un produit cartésien
Considérons deux ![]() espaces vectoriels
espaces vectoriels ![]() L’ensemble des couples
L’ensemble des couples ![]() avec
avec ![]() et
et ![]() est noté
est noté ![]() C’est le produit cartésien de
C’est le produit cartésien de ![]() par
par ![]()
On munit cet ensemble d’une structure de ![]() espace vectoriel, en décrétant que :
espace vectoriel, en décrétant que :
- pour tout
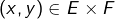 et tout
et tout 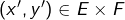 :
: (S)
![Rendered by QuickLaTeX.com \[\left(x,y\right)+\left(x',y'\right)=\left(x+x',y+y'\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-af62b572d4e7233e313071e3928ec672_l3.png)
- pour tout
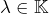 et tout
et tout 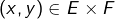 :
:(P)
![Rendered by QuickLaTeX.com \[\lambda\left(x,y\right)=\left(\lambda x,\thinspace\lambda y\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bc98cd27dd39b91d595f39b5434be65c_l3.png)
Précisons que le vecteur nul de ![]() est le couple
est le couple ![]()

La notation utilisée dans la formule (S) est abusive, car le symbole ![]() est utilisé pour désigner trois opérations a priori distinctes :
est utilisé pour désigner trois opérations a priori distinctes :
- l’addition dans
 ,
, - l’addition dans
 ,
, - l’addition dans
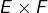
Il est essentiel d’en être conscient(e). Sans compter que, dans ce contexte, le symbole ![]() désignera aussi l’addition dans
désignera aussi l’addition dans ![]() …
…
Et l’on pourrait formuler une remarque similaire pour la formule (P).
Cela dit, énonçons la :
Règle B
Si ![]() sont de dimensions finies, alors
sont de dimensions finies, alors ![]() aussi et :
aussi et :
![]()
Preuve (cliquer pour déplier / replier)
Notons ![]() et
et ![]() Si l’on considère une base
Si l’on considère une base ![]() de
de ![]() ainsi qu’une base
ainsi qu’une base ![]() de
de ![]() alors la famille :
alors la famille :
![]()
On vérifie en effet que ![]() est libre et génératrice de
est libre et génératrice de ![]() :
:
➢ LIBRE car si ![]() sont des scalaires vérifiant :
sont des scalaires vérifiant :
![]()
![Rendered by QuickLaTeX.com \[\left(\sum_{i=1}^{p}\lambda_{i}e_{i},\thinspace\sum_{j=1}^{n}\mu_{j}f_{j}\right)=\left(0_{E},0_{F}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f12830b8355f6757a5a89f9a1cb4ea24_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{p}\lambda_{i}e_{i}=0_{E}\qquad\text{et}\qquad\sum_{j=1}^{n}\mu_{j}f_{j}=0_{F}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-27bcb60b72e47a96e4ac56215505790a_l3.png)
![]()
➢ GENERATRICE de ![]() car tout vecteur de
car tout vecteur de ![]() se présente sous la forme d’un couple
se présente sous la forme d’un couple ![]() avec
avec ![]() et
et ![]() or
or ![]() se décompose dans la base
se décompose dans la base ![]() et
et ![]() se décompose dans la base
se décompose dans la base ![]() :
:
![Rendered by QuickLaTeX.com \[x=\sum_{i=1}^{p}x_{i}e_{i}\qquad\text{et}\qquad y=\sum_{j=1}^{n}y_{j}f_{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bd28ec01512896ec7e9ed0bdcd999fee_l3.png)
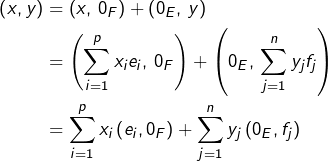
Remarque
Il en résulte par récurrence que si ![]() et si
et si ![]() sont des
sont des ![]() espaces vectoriels de dimensions finies, alors il en va de même pour
espaces vectoriels de dimensions finies, alors il en va de même pour ![]() et :
et :
![Rendered by QuickLaTeX.com \[\boxed{\dim\left(\prod_{k=1}^{r}E_{k}\right)=\sum_{k=1}^{r}\dim\left(E_{k}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bc39dc458d0e579d31c1fd7f54c51d2a_l3.png)
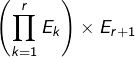
Exemple B
L’espace ![]() est de dimension
est de dimension ![]()
4 – Utilisation d’un isomorphisme
Règle C
Soient ![]() deux
deux ![]() espaces vectoriels isomorphes.
espaces vectoriels isomorphes.
Si l’un d’eux est de dimension finie, alors l’autre aussi et leurs dimensions sont égales.
Ce résultat découle du double-lemme suivant :
Double-Lemme
Soient ![]() deux
deux ![]() espaces vectoriels et soit
espaces vectoriels et soit ![]()
- Si
 est injective, alors
est injective, alors  transforme toute famille libre de vecteurs de
transforme toute famille libre de vecteurs de  en une famille libre de vecteurs de
en une famille libre de vecteurs de 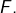
- Si
 est surjective, alors
est surjective, alors  transforme tout famille génératrice de
transforme tout famille génératrice de  en une famille génératrice de
en une famille génératrice de 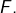
Preuve du double lemme (cliquer pour déployer)
Pour le premier point …
Considérons une famille libre ![]() de vecteurs de
de vecteurs de ![]() et des scalaires
et des scalaires ![]() tels que :
tels que :
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{r}\lambda_{i}\thinspace u\left(x_{i}\right)=0_{F}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1bbbb660e852fa5a17928b6b5975b1e3_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{r}\lambda_{i}\thinspace x_{i}\in\ker\left(u\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d4b24172e7e1681b86cb4c9e37ee3396_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=1}^{r}\lambda_{i}x_{i}=0_{E}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-63edb5c9d4b3ccd24890ebee13596f90_l3.png)
Pour le second point …
Donnons-nous une famille ![]() génératrice de
génératrice de ![]() et soit
et soit ![]() Comme
Comme ![]() est surjective, il existe
est surjective, il existe ![]() tel que
tel que ![]() On peut alors exprimer
On peut alors exprimer ![]() sous la forme d’une combinaison linéaire des
sous la forme d’une combinaison linéaire des ![]() :
:
![Rendered by QuickLaTeX.com \[\exists\left(\alpha_{1},\cdots,\alpha_{s}\right)\in\mathbb{K}^{s};\thinspace x=\sum_{i=1}^{s}\alpha_{i}e_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2c36484757efaff9274d22d4b72640f7_l3.png)
![Rendered by QuickLaTeX.com \[y=\sum_{i=1}^{s}\alpha_{i}\thinspace u\left(e_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8931d241d5242cf468b9df3a1ebfdcbc_l3.png)
Maintenant que notre double-lemme est établi, la règle C devient claire. En effet, si ![]() est un isomorphisme et si
est un isomorphisme et si ![]() est de dimension
est de dimension ![]() alors une base
alors une base ![]() de
de ![]() est transformée par
est transformée par ![]() en une famille libre (parce que
en une famille libre (parce que ![]() est une injection linéaire) et aussi en une famille génératrice de
est une injection linéaire) et aussi en une famille génératrice de ![]() (parce que
(parce que ![]() est une surjection linéaire).
est une surjection linéaire).
Moralité, la famille ![]() est une base de
est une base de ![]() et donc (cf. règle A) :
et donc (cf. règle A) : ![]()
Ce mécanisme sera utilisé dans chacune des trois sections suivantes.
Mais donnons-en déjà une application significative.
Exemple C-1
Etant donné ![]() intéressons-nous à l’ensemble
intéressons-nous à l’ensemble ![]() des suites
des suites ![]() à termes dans
à termes dans ![]() qui vérifient la relation de récurrence :
qui vérifient la relation de récurrence :
(![]() )
) ![]()
Pour cela, commençons par observer que si ![]() désigne l’endomorphisme de décalage (le shift, comme on dit outre-manche), c’est-à-dire l’application
désigne l’endomorphisme de décalage (le shift, comme on dit outre-manche), c’est-à-dire l’application
![]()
![]()
Maintenant, considérons l’application
![]()
Il est facile (non détaillé) de prouver que ![]() est linéaire et bijective. Il en résulte aussitôt que :
est linéaire et bijective. Il en résulte aussitôt que :
![]()
Remarque
Cet exemple se généralise. Si ![]() et si
et si ![]() alors l’espace des suites
alors l’espace des suites ![]() vérifiant la relation
vérifiant la relation
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N},\thinspace u_{n+r}+\sum_{i=0}^{r-1}a_{i}\thinspace u_{n+i}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6cbb1e1a3ffd96c117e1c30d166a18ca_l3.png)
5 – Dimension d’une somme
Rappelons que si ![]() est un
est un ![]() espace vectoriel et si
espace vectoriel et si ![]() sont deux sous-espaces vectoriels de
sont deux sous-espaces vectoriels de ![]() alors
alors ![]() désigne l’ensemble des vecteurs de
désigne l’ensemble des vecteurs de ![]() qui sont la somme d’un vecteur de
qui sont la somme d’un vecteur de ![]() et d’un vecteur de
et d’un vecteur de ![]() :
:
![]()

Les notations ![]() et
et ![]() désignent donc le même ensemble, mais la seconde indique qu’une condition supplémentaire (jeu de mots) d’unicité est remplie !
désignent donc le même ensemble, mais la seconde indique qu’une condition supplémentaire (jeu de mots) d’unicité est remplie !
Le but de cette section est d’obtenir une formule pour ![]() lorsque
lorsque ![]() et
et ![]() sont de dimensions finies (il n’est pas utile de supposer que la dimension de
sont de dimensions finies (il n’est pas utile de supposer que la dimension de ![]() est finie).
est finie).
Procédons en deux temps.
1ère étape
Supposons la somme ![]() directe. Sous cette hypothèse, l’application
directe. Sous cette hypothèse, l’application
![]()
Détail
Linéarité
Soient ![]()
![]() et
et ![]() Alors :
Alors :
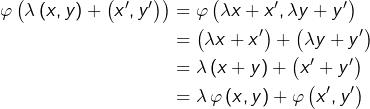
Bijectivité
Tout vecteur de ![]() peut, par définition, s’écrire de façon unique sous la forme
peut, par définition, s’écrire de façon unique sous la forme ![]() avec
avec ![]() et
et ![]() autrement dit tout élément de l’ensemble d’arrivée de
autrement dit tout élément de l’ensemble d’arrivée de ![]() possède un unique antécédent. C’est la définition d’une bijection.
possède un unique antécédent. C’est la définition d’une bijection.
Ceci permet d’appliquer la règle B et la règle C : comme ![]() est de dimension finie, alors
est de dimension finie, alors ![]() aussi et les dimensions sont les mêmes. Concluons :
aussi et les dimensions sont les mêmes. Concluons :
![]()
2ème étape
Dans le cas général, l’idée consiste à se ramener à une somme directe, grâce au lemme suivant.
Lemme
Soient ![]() deux sous-espaces vectoriels de
deux sous-espaces vectoriels de ![]()
Etant donné un supplémentaire ![]() de
de ![]() dans
dans ![]() :
:
![]()
Preuve (cliquer pour déplier / replier)
Si ![]() alors il existe
alors il existe ![]() tel que
tel que ![]() Puis comme
Puis comme ![]() il existe
il existe ![]() et
et ![]() tels que
tels que ![]() De ce fait :
De ce fait :
![]()
Pour finir, la somme ![]() est directe puisque, comme
est directe puisque, comme ![]() :
:
![]()
On en déduit la :
Règle D (formule de Grassmann)
Soit ![]() un
un ![]() espace vectoriel et soient
espace vectoriel et soient ![]() des sous-espaces vectoriels de
des sous-espaces vectoriels de ![]() de dimensions finies. Alors :
de dimensions finies. Alors :
![]()

Remarque
Cette formule évoque celle donnant le cardinal de l’union de deux ensembles finis. Mais la comparaison s’arrête là …
En effet, étant donnés trois sous-espaces ![]() de dimensions finies, la formule :
de dimensions finies, la formule :
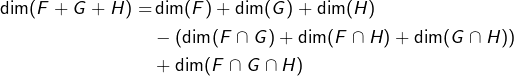
Comme contre-exemple, on peut proposer, pour ![]() :
:
![]()
Exemple D-1
Considérons un espace ![]() de dimension finie
de dimension finie ![]() et deux hyperplans
et deux hyperplans ![]() et
et ![]() de
de ![]() (ce sont simplement des sous-espaces vectoriels de dimension
(ce sont simplement des sous-espaces vectoriels de dimension ![]()
Calculons la dimension de ![]() en distinguant deux cas.
en distinguant deux cas.
➢ cas 1 : ![]()
Il est évident que ![]() puisque
puisque ![]()
➢ cas 2 : ![]()
Aucun des deux hyperplans n’est inclus dans l’autre (une inclusion entraînerait, vue l’égalité des dimensions, que les deux hyperplans sont confondus). Soit ![]() tel que
tel que ![]() La somme
La somme ![]() est alors directe (puisque
est alors directe (puisque ![]() et sa dimension est donc :
et sa dimension est donc :
![]()
On applique maintenant la formule de Grassmann :
![]()
![]()
En conclusion, si ![]() et
et ![]() sont deux hyperplans d’un espace de dimension
sont deux hyperplans d’un espace de dimension ![]() alors :
alors :
![Rendered by QuickLaTeX.com \[\boxed{\dim\left(A\cap B\right)=\left\{ \begin{array}{cc}n-1 & \text{si }A=B\\n-2 & \text{sinon}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cd847bafd5f624976f3abb91d90857bb_l3.png)
6 – La formule du rang
Considérons deux ![]() espaces vectoriels
espaces vectoriels ![]() et une application linéaire
et une application linéaire ![]()
Règle E (théorème du rang)
Si ![]() est de dimension finie alors
est de dimension finie alors ![]() est aussi de dimension finie et :
est aussi de dimension finie et :
![]()
L’égalité ci-dessus porte le nom de formule du rang.
Ce résultat important est démontré dans cet article, auquel vous pouvez vous reporter, si nécessaire.
Exemple E-1
Considérons l’application linéaire :
![]()
![]()
La condition ![]() étant conséquence des deux autres :
étant conséquence des deux autres :
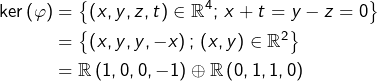
et donc (somme directe de deux droites vectorielle : cf. section 5) :
![]()
![]()
Exemple E-2
Considérons un ![]() espace vectoriel
espace vectoriel ![]() de dimension
de dimension ![]() et cherchons la valeur maximale du rang d’un endomorphisme
et cherchons la valeur maximale du rang d’un endomorphisme ![]() vérifiant
vérifiant ![]()
Analysons la situation … Si ![]() est un tel endomorphisme, alors
est un tel endomorphisme, alors ![]() donc, en passant aux dimensions :
donc, en passant aux dimensions :
![]()
![]()
(![]() )
) ![]()
Si l’on construit un endomorphisme ![]() vérifiant
vérifiant ![]() et pour lequel
et pour lequel ![]() est une égalité, on aura fini. Et c’est possible …
est une égalité, on aura fini. Et c’est possible …
Soit ![]() une base de
une base de ![]() . Définissons
. Définissons ![]() par sa matrice
par sa matrice ![]() dans
dans ![]() :
:
➤ Si ![]() est pair,
est pair, ![]() :
:
![]()
➤ Si ![]() est impair,
est impair, ![]() :
:
![]()
Par exemple :
![Rendered by QuickLaTeX.com \[\text{si }n=4\text{ :}\qquad M=\left[\begin{array}{cccc}0 & 1 & 0 & 0\\0 & 0 & 0 & 0\\0 & 0 & 0 & 1\\0 & 0 & 0 & 0\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3e691fb78caed0583c6c07af92876d43_l3.png)
![Rendered by QuickLaTeX.com \[\text{si }n=5\text{ :}\qquad M=\left[\begin{array}{ccccc}0 & 1 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 1 & 0\\0 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 0\end{array}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2beacac4feb18e7cd08365f361526dea_l3.png)
Exemple E-3
Nous avons vu plus haut la formule de Grassmann, qui donne la dimension d’une somme de deux sev de dimensions finies. Voici une nouvelle preuve de ce résultat.
Notons ![]() un
un ![]() espace vectoriel et
espace vectoriel et ![]() deux sous espaces de dimensions finies.
deux sous espaces de dimensions finies.
Considérons l’application
![]()
Le noyau de ![]() est :
est :
![]()
![]()
![]()
La formule du rang montre alors que :
![]()
![]()
7 – Dimension des espaces d’applications linéaires
Très utile aussi, une formule donnant la dimension de l’espace des applications linéaires de ![]() vers
vers ![]() où
où ![]() sont deux
sont deux ![]() espaces vectoriels de dimensions finies.
espaces vectoriels de dimensions finies.
En fait, nous avons déjà établi — quoiqu’indirectement — cette formule, puisque nous avons vu que ![]()
Or, si l’on note ![]()
![]() ,
, ![]() une base de
une base de ![]() et
et ![]() une base de
une base de ![]() alors l’application
alors l’application
![]()
Autrement dit :
(![]() )
) ![]()
On peut établir directement la formule ![]() en exploitant le fait qu’une application linéaire est déterminée par les images des vecteurs d’une base. Ce principe (qui conduit à la notion de matrice d’une application linéaire relativement à un couple de bases) est étudié en détail dans cet article.
en exploitant le fait qu’une application linéaire est déterminée par les images des vecteurs d’une base. Ce principe (qui conduit à la notion de matrice d’une application linéaire relativement à un couple de bases) est étudié en détail dans cet article.
Fixons donc une base ![]() de
de ![]() et considérons l’application
et considérons l’application
![]()
![]()
En outre ![]() est linéaire (vérification aisée, non détaillée). Il s’agit donc d’un isomorphisme.
est linéaire (vérification aisée, non détaillée). Il s’agit donc d’un isomorphisme.
A nouveau, la règle C s’applique et permet de conclure que :
![]()
Remarque
Un cas particulier important est celui du dual d’un ![]() espace vectoriel
espace vectoriel ![]()
Il s’agit de l’espace ![]() des formes linéaires sur
des formes linéaires sur ![]() souvent noté
souvent noté ![]() D’après ce qui précède, et vu que
D’après ce qui précède, et vu que ![]() on voit que :
on voit que :
![]()
8 – Et lorsque la dimension est infinie ?
La question soulevée dans cette section est la suivante :
Comment prouver qu’un espace vectoriel donné est de dimension infinie ?
Lorsqu’un ![]() espace vectoriel
espace vectoriel ![]() est de dimension finie
est de dimension finie ![]() toute famille libre est finie et comporte au plus
toute famille libre est finie et comporte au plus ![]() vecteurs (ceci découle du lemme de Steinitz, qui est expliqué en détail dans cette vidéo).
vecteurs (ceci découle du lemme de Steinitz, qui est expliqué en détail dans cette vidéo).
Par conséquent :
Règle F
Pour établir qu’un espace est de dimension infinie, il suffit de prouver l’existence de familles libres de cardinal arbitraire.
Règle F-Bis
Pour établir qu’un espace est de dimension infinie, il suffit d’exhiber un sous-espace de dimension infinie.
Plus généralement : soient ![]() et
et ![]() des
des ![]() espaces vectoriels,
espaces vectoriels, ![]() étant de dimension infinie. S’il existe une application linéaire injective de
étant de dimension infinie. S’il existe une application linéaire injective de ![]() dans
dans ![]() alors
alors ![]() est de dimension infinie.
est de dimension infinie.
Voyons quelques exemples d’utilisation de ces règles …
Exemple F-1
Pour tout entier ![]() la famille de polynômes
la famille de polynômes ![]() est libre dans l’espace
est libre dans l’espace ![]() et comporte
et comporte ![]() vecteurs. Comme
vecteurs. Comme ![]() peut être choisie de façon arbitraire, ceci montre que
peut être choisie de façon arbitraire, ceci montre que ![]() est de dimension infinie.
est de dimension infinie.
Exemple F-2
Dans cette vidéo, on prouve que, pour tout ![]() la famille constituée des applications :
la famille constituée des applications :
![]()
Cet espace est donc de dimension infinie.
Bien entendu, le choix de l’intervalle ![]() ne joue aucun rôle particulier et la continuité peut être remplacée par une condition plus forte (voir exemple suivant).
ne joue aucun rôle particulier et la continuité peut être remplacée par une condition plus forte (voir exemple suivant).
Exemple F-3
Pour tout intervalle ![]() de longueur non nulle, l’espace des applications polynomiales de
de longueur non nulle, l’espace des applications polynomiales de ![]() dans
dans ![]() est de dimension infinie. Il en résulte que l’espace
est de dimension infinie. Il en résulte que l’espace ![]() des applications indéfiniment dérivables de
des applications indéfiniment dérivables de ![]() dans
dans ![]() (qui contient le précédent) est de dimension infinie.
(qui contient le précédent) est de dimension infinie.
Même chose pour l’espace des applications de classe ![]() (pour tout entier
(pour tout entier ![]() de
de ![]() dans
dans ![]()
Même chose pour l’espace ![]() de toutes les applications de
de toutes les applications de ![]() dans
dans ![]()
On a donc une chaîne d’espaces emboîtés, tous de dimension infinie :
![]()
Exemple F-4
Soient deux réels ![]()
Notons ![]() l’espace vectoriels des applications en escalier de
l’espace vectoriels des applications en escalier de ![]() dans
dans ![]()
Rappelons qu’une application ![]() est dite en escalier lorsqu’il existe une subdivision
est dite en escalier lorsqu’il existe une subdivision ![]() telle que la restriction de
telle que la restriction de ![]() à chacun des intervalles
à chacun des intervalles ![]() (pour
(pour ![]() soit constante.
soit constante.
Si l’on pose, pour tout ![]() :
:
![]()
De plus, si ![]() sont tous distincts, la famille
sont tous distincts, la famille ![]() est libre.
est libre.
Il s’ensuit que ![]() est de dimension infinie.
est de dimension infinie.
On peut en déduire que l’espace des applications de ![]() dans
dans ![]() qui ne prennent qu’un nombre fini de valeurs est aussi de dimension infinie, puisqu’il contient
qui ne prennent qu’un nombre fini de valeurs est aussi de dimension infinie, puisqu’il contient ![]()
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
