
L’objet de cet article est de prouver un cas très particulier du théorème de Fubini, en utilisant un arsenal théorique aussi restreint que possible. Plus précisément, nous allons établir le :
Théorème 
Soit ![]() une application continue. Alors :
une application continue. Alors :
![]()
Pour cela, nous aurons besoin de trois ingrédients principaux :
- Notion de continuité uniforme et théorème de Heine,
- Sommes de Riemann : définition et théorème de convergence dans le cas continu,
- Interversion limite / intégrale pour une suite uniformément convergente de fonctions continues sur un segment.
Afin de rendre le présent texte aussi « self-contained » que possible (désolé pour l’anglicisme, mais je n’ai pas trouvé mieux), j’ai rassemblé deux de ces trois ingrédients en fin d’article : il s’agit, d’une part, du théorème de convergence des sommes de Riemann (cf. section 4) et, d’autre part, du théorème d’interversion limite / intégrale (cf. section 5).
Quant à la continuité uniforme, elle fait l’objet d’un autre article, auquel on pourra se reporter si nécessaire.
1 – Observation préliminaire
Etant donnée ![]() continue, montrons la continuité de l’application :
continue, montrons la continuité de l’application :
![]()
Pour cela, fixons ![]() ainsi que
ainsi que ![]() Comme
Comme ![]() est continue sur le compact
est continue sur le compact ![]() elle est uniformément continue (théorème de Heine).
elle est uniformément continue (théorème de Heine).
Il existe donc ![]() tel que pour tout
tel que pour tout ![]() et tout
et tout ![]() :
:
![]()
Par conséquent, dès que ![]() :
:
![]()
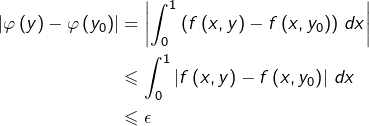
Ceci prouve la continuité de ![]() en
en ![]() pour tout
pour tout ![]()
Pour des raisons identiques, l’application :
![]()
est continue, elle aussi.
Cette observation préliminaire montre que, dans le théorème ![]() , les deux membres de l’égalité sont bien définis : ce sont des intégrales de fonctions continues sur le segment
, les deux membres de l’égalité sont bien définis : ce sont des intégrales de fonctions continues sur le segment ![]() Une théorie élémentaire de l’intégration (où l’on se borne à intégrer des fonctions continues sur un segment) est donc suffisante pour ce contexte.
Une théorie élémentaire de l’intégration (où l’on se borne à intégrer des fonctions continues sur un segment) est donc suffisante pour ce contexte.
2 – Preuve du théorème 
Les applications ![]() et
et ![]() sont celles introduites à la section précédente.
sont celles introduites à la section précédente.
En appliquant le théorème des sommes de Riemann (voir section 4) à l’application ![]() on obtient :
on obtient :
![Rendered by QuickLaTeX.com \[\int_{0}^{1}\left(\int_{0}^{1}f\left(x,y\right)\thinspace dx\right)\thinspace dy & = & \lim_{n\rightarrow\infty}\frac{1}{n}\sum_{k=1}^{n}\int_{0}^{1}f\left(x,\frac{k}{n}\right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-099e869551e43bd4d7ab4eaea651e1de_l3.png)
donc, par linéarité de l’intégrale :
![Rendered by QuickLaTeX.com \[\int_{0}^{1}\left(\int_{0}^{1}f\left(x,y\right)\thinspace dx\right)\thinspace dy=\lim_{n\rightarrow\infty}\int_{0}^{1}\left(\frac{1}{n}\sum_{k=1}^{n}f\left(x,\frac{k}{n}\right)\right)\thinspace dx\qquad\left(\diamondsuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-31d3a0581fec2849e5b9857619c781f5_l3.png)
Posons maintenant, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ J_{n}\left(x\right)=\frac{1}{n}\sum_{k=1}^{n}f\left(x,\frac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9e5283e8ea6a8600c0d9f5fb7475e44f_l3.png)
Etant donné ![]() il s’agit de montrer que :
il s’agit de montrer que :
![]()
D’après la relation de Chasles, on a pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ J_{n}\left(x\right)-\psi\left(x\right)=\sum_{k=1}^{n}\int_{\left(k-1\right)/n}^{k/n}\left(f\left(x,\frac{k}{n}\right)-f\left(x,y\right)\right)\thinspace dy\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bdc5b3e98dbd33709b53d873d5d9f120_l3.png)
Reprenons le réel ![]() donné par l’uniforme continuité de
donné par l’uniforme continuité de ![]() (voir calcul de la section 1) et notons
(voir calcul de la section 1) et notons ![]() la partie entière par excès de
la partie entière par excès de ![]() . Si
. Si ![]() alors pour tout
alors pour tout ![]() et tout
et tout ![]() :
:
![]()
![]()
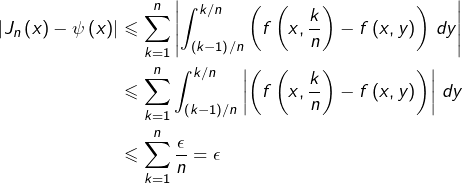
Comme ceci est valable quel que soit ![]() on a prouvé
on a prouvé ![]()
On peut maintenant appliquer à la suite ![]() le théorème d’interversion limite / intégrale pour une suite uniformément convergente de fonctions continues (voir section 5). On obtient :
le théorème d’interversion limite / intégrale pour une suite uniformément convergente de fonctions continues (voir section 5). On obtient :
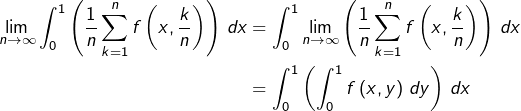
et donc, en faisant le lien avec ![]() on démontre le théorème
on démontre le théorème ![]()
3 – Application au calcul d’un intégrale
Vous avez certainement rencontré des exercices où l’on demande de calculer une somme double 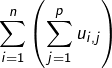 et où la clé réside dans l’interversion des sommes.
et où la clé réside dans l’interversion des sommes.
Avec les intégrales, c’est la même idée … quoique (comme on l’a vu plus haut) l’interversion des intégrales soit significativement plus délicate à justifier !
Considérons, pour tout ![]() :
:
![]()
Alors, d’après le théorème ![]() :
:
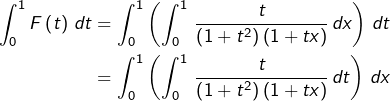
![]()
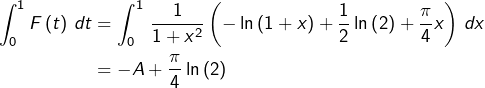
![Rendered by QuickLaTeX.com \[\boxed{A=\int_{0}^{1}\frac{\ln\left(1+x\right)}{1+x^{2}}\thinspace dx}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0d9408b2f7bb84a91e5f186106faf647_l3.png)
Par ailleurs (et de façon plus directe) :
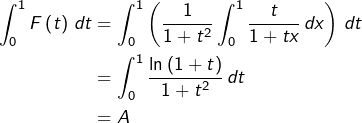
![]()
![Rendered by QuickLaTeX.com \[ \boxed{\int_{0}^{1}\,\frac{\ln\left(1+x\right)}{1+x^{2}}\,dx=\frac{\pi}{8}\ln\left(2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8f442c6e150898f67ce46d8f94952196_l3.png)
L’interversion des deux intégrales a permis de calculer ![]()
Challenge
Sauriez-vous calculer ![]() autrement ? (par un moyen plus simple et / ou plus direct).
autrement ? (par un moyen plus simple et / ou plus direct).
Si oui, faites-moi signe via le formulaire de contact et je mettrais votre solution en ligne … si elle est correcte 😉
4 – Un mot sur les sommes de Riemann
La preuve présentée à la section 2 reposait notamment sur un théorème de convergence des sommes de Riemann, dont voici l’énoncé :
Théorème
Soit ![]() une application continue. Alors :
une application continue. Alors :
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow\infty}\frac{1}{n}\sum_{k=1}^{n}f\left(\frac{k}{n}\right)=\int_{0}^{1}f\left(x\right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8bf6dcdb0db8304350cd7327f160cc3c_l3.png)
Attention de ne pas confondre sommes de Riemann et séries de Riemann.

Notons, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[S_{n}=\frac{1}{n}\sum_{k=1}^{n}f\left(\frac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2e14d2b3d4c1e9469950026c29049ef8_l3.png)
![]()
Il s’agit de prouver que ![]() Avec la relation de Chasles, on voit que :
Avec la relation de Chasles, on voit que :
![Rendered by QuickLaTeX.com \[\int_{0}^{1}f\left(x\right)\thinspace dx = \sum_{k=1}^{n}\int_{\left(k-1\right)/n}^{k/n}f\left(x\right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-596d097a04bd9a9be1512348bc660586_l3.png)
![Rendered by QuickLaTeX.com \[ \Delta_{n}=\sum_{k=1}^{n}\int_{\left(k-1\right)/n}^{k/n}\left(f\left(x\right)-f\left(\frac{k}{n}\right)\right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bcbdef012e794c5bd65126b536ba80ed_l3.png)
![Rendered by QuickLaTeX.com \[ \left|\Delta_{n}\right|\leqslant\sum_{k=1}^{n}\int_{\left(k-1\right)/n}^{k/n}\left|f\left(x\right)-f\left(\frac{k}{n}\right)\right|\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3c65a3ee80569b4f9347b9042ca4072f_l3.png)
Fixons ![]() D’après le théorème de Heine, il existe
D’après le théorème de Heine, il existe ![]() tel que :
tel que :
![]()
Par conséquent, dès que ![]() on a pour tout
on a pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[ \left|\Delta_{n}\right|\leqslant\sum_{k=1}^{n}\frac{\epsilon}{n}=\epsilon\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4a3cac4c6c43df2d25108c6d9349cda7_l3.png)
Le théorème de convergence des sommes de Riemann est démontré.
On pourra trouver, dans cette fiche d’exercices, divers exemples d’utilisation de ce résultat.
5 – Un mot sur l’interversion limite / intégrale
Il existe plusieurs théorèmes donnant des conditions suffisantes pour garantir une formule du genre :
![]()
Celui qui nous intéresse ici est le suivant :
Théorème 
Soit ![]() une suite d’applications continues de
une suite d’applications continues de ![]() dans
dans ![]() qui converge uniformément sur
qui converge uniformément sur ![]() vers une application
vers une application ![]() Alors :
Alors :
![]()
Autrement dit : la limite de l’intégrale et l’intégrale de la limite sont égales.
Avant de démontrer quoique ce soit, il faut bien voir qu’une hypothèse de convergence simple serait insuffisante et ceci pour deux raisons :
- d’une part, la limite simple d’une suite d’applications continues n’est pas nécessairement continue, ce qui soulève une première difficulté (on s’est fixé une contrainte en début d’article, en se limitant à la théorie de l’intégration des fonctions continues sur un segment),
- d’autre part, même si
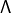 est continue, l’égalité annoncée n’est pas vraie en général.
est continue, l’égalité annoncée n’est pas vraie en général.
Concernant cette seconde objection, voici un …
Contre-exemple classique
On considère, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[ u_{n}:\left[0,1\right]\rightarrow\mathbb{R},\thinspace x\mapsto\left\{\begin{array}{ccc} 2n^{2}x & \text{si} & 0\leqslant x\leqslant\frac{1}{2n}\\\\ -2n^{2}\left(x-\frac{1}{n}\right) & \text{si} & \frac{1}{2n}<x\leqslant\frac{1}{n}\\\\ 0 & \text{si} & \frac{1}{n}<x\leqslant1\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a1197b270e9affb5c9efd747b8dd5125_l3.png)
Il est clair que ![]() est une suite d’applications continues sur
est une suite d’applications continues sur ![]()
Cette suite converge simplement vers l’application nulle; en effet ![]() pour tout
pour tout ![]() et si
et si ![]() alors
alors ![]() dès que
dès que ![]() de sorte que la suite
de sorte que la suite ![]() est « mieux » que convergente : elle est stationnaire ! L’intégrale de la limite est donc nulle.
est « mieux » que convergente : elle est stationnaire ! L’intégrale de la limite est donc nulle.
Mais la limite de l’intégrale ne l’est pas ! En effet, pour tout entier ![]() :
:
![]()
![]()
L’illustration dynamique ci-dessous montre le graphe de ![]() pour
pour ![]() :
:
Graphe de  : l’aire du triangle bleu est indépendante de n
: l’aire du triangle bleu est indépendante de n
Venons-en maintenant à la preuve du théorème ![]()
Déjà, ![]() est continue car limite uniforme d’une suite d’applications continues (ce qui donne un sens à l’intégrale de
est continue car limite uniforme d’une suite d’applications continues (ce qui donne un sens à l’intégrale de ![]() Il s’agit ensuite de prouver que :
Il s’agit ensuite de prouver que :
![]()
![Rendered by QuickLaTeX.com \begin{equation*}\begin{split}\left|\int_{0}^{1}\left(u_{n}\left(x\right)-\Lambda\left(x\right)\right)\thinspace dx\right| & \leqslant \int_{0}^{1}\left|u_{n}\left(x\right)-\Lambda\left(x\right)\right|\thinspace dx\\& \leqslant \sup_{x\in\left[0,1\right]}\left|u_{n}\left(x\right)-\Lambda\left(x\right)\right|\end{split}\end{equation*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-e49ba2c0636a372f5117e1cb73611247_l3.png)
Solutions des internautes pour le challenge
Solution proposée le 11/08/2019 par Simon Billouet
On cherche à calculer :
![]()
Effectuons le changement de variable (clairement licite) ![]() .
.
On a donc : ![]() soit
soit ![]() .
.
De plus ![]() . Lorsque
. Lorsque ![]() varie entre 0 et 1,
varie entre 0 et 1, ![]() varie entre 0 et
varie entre 0 et ![]() . Ainsi :
. Ainsi :
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{I=\frac{\pi\ln(2)}{8}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b0a875dfc789d9571e562dfa94f15d71_l3.png)
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
