Voici un énoncé (pas le plus général) du théorème de convergence des sommes de Riemann :
Théorème
Soit ![Rendered by QuickLaTeX.com f:\left[a,b\right]\rightarrow\mathbb{R}](https://math-os.com/wp-content/ql-cache/quicklatex.com-d4da71c7eb5c9e6aa61c58d77d717be2_l3.png) une application intégrable au sens au de Riemann.
une application intégrable au sens au de Riemann.
Si l’on pose pour tout 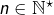 :
:
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{b-a}{n}\sum_{k=1}^{n}f\left(a+\dfrac{k\left(b-a\right)}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d88a99dfa82072b20765767fc1233188_l3.png)
alors :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}S_{n}=\int_{a}^{b}f\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7ce8c5e89d5c0ddcea0d0f05bb7588f3_l3.png)
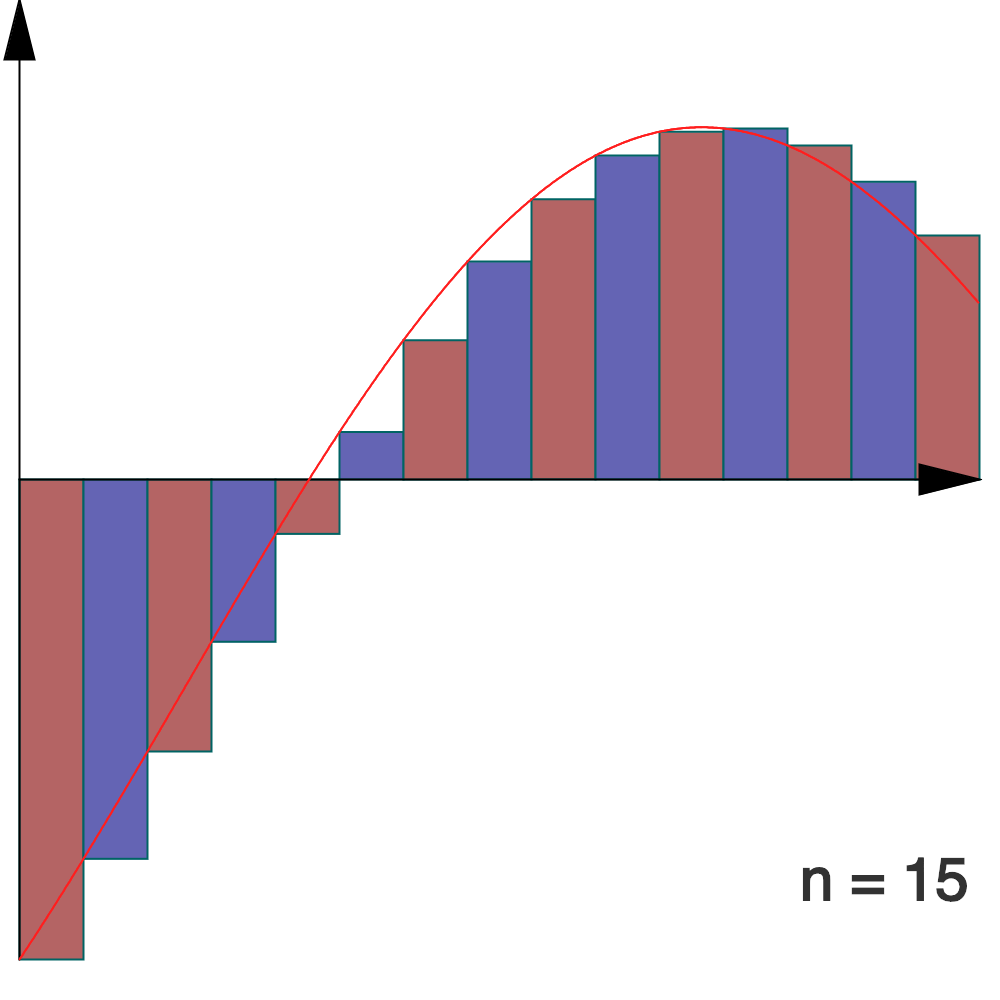
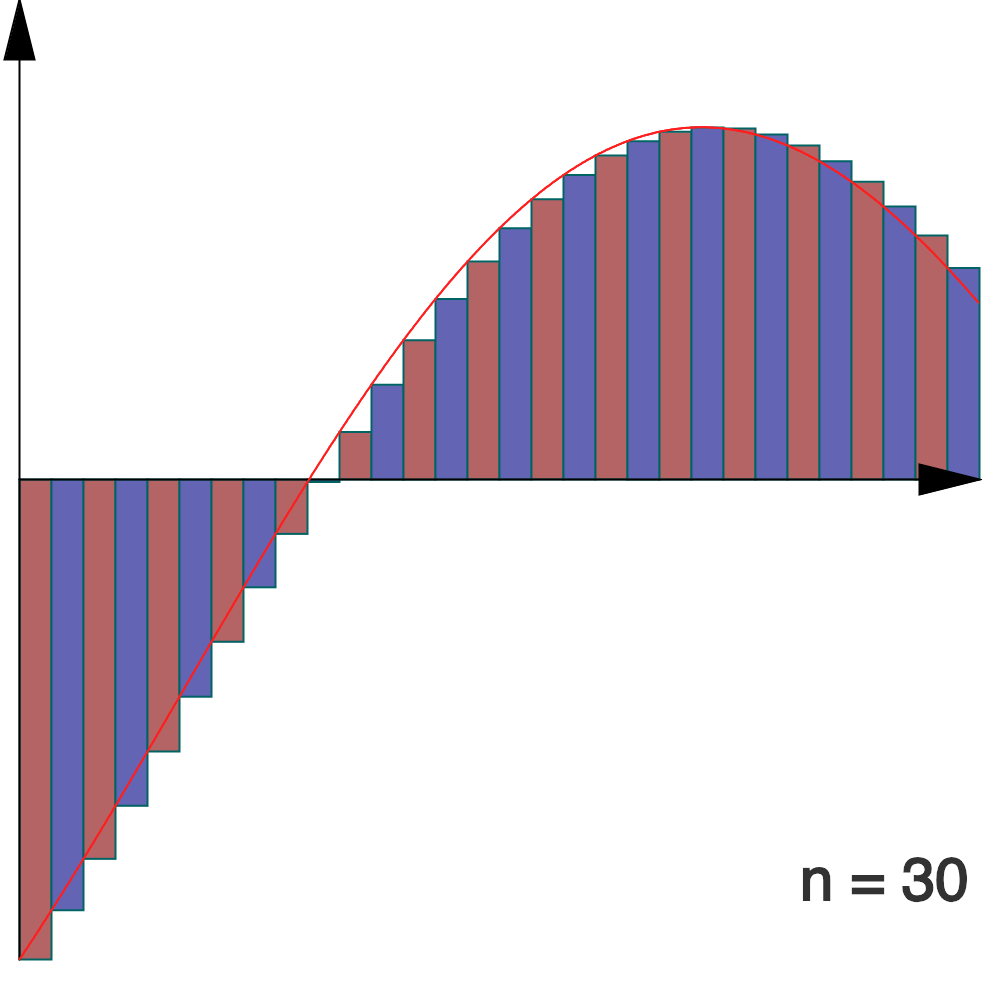
Interprétation géométrique :
Lorsque n tend vers l’infini, la somme des aires algébriques des rectangles associés à la subdivision régulière de ![Rendered by QuickLaTeX.com \left[a,b\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c1c9b62f4ffe493505d6566104a9b311_l3.png) en n « tranches » converge vers l’intégrale de f.
en n « tranches » converge vers l’intégrale de f.
Dans la vidéo ci-dessous, qui est disponible sur la chaine YouTube du blog Math-OS, on démontre ce théorème pour  de classe
de classe 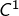 et aussi (un peu plus généralement et en faisant intervenir le théorème de Heine) pour
et aussi (un peu plus généralement et en faisant intervenir le théorème de Heine) pour  continue :
continue :
On admettra ici que le résultat persiste sous la seule hypothèse que  est intégrable au sens de Riemann.
est intégrable au sens de Riemann.
Dans ce qui suit, quelques exemples d’utilisation de ce théorème sont présentés en détail.
Encore deux remarques avant de commencer :
Remarque 1
Dans l’énoncé du théorème, on peut remplacer « somme de Riemann à droite » par « somme de Riemann à gauche », c’est-à-dire 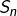 par :
par :
![Rendered by QuickLaTeX.com \[S'_{n}=\dfrac{b-a}{n}\sum_{k=0}^{n-1}f\left(a+\dfrac{k\left(b-a\right)}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-50f4f924eda56cdb6b4bb2ea56bf561e_l3.png)
Vu que :
![Rendered by QuickLaTeX.com \[S_{n}-S'_{n}=\dfrac{b-a}{n}\left(f\left(b\right)-f\left(a\right)\right)\underset{n\rightarrow+\infty}{\longrightarrow}0 \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-12bca1fab26d790b82ceb79dfee1863c_l3.png)
il est clair qu’on a aussi :
![Rendered by QuickLaTeX.com \[ \lim_{n\rightarrow+\infty}S'_{n}=\int_{a}^{b}f\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c35ee8e54047783baa7a413e74fbe23c_l3.png)
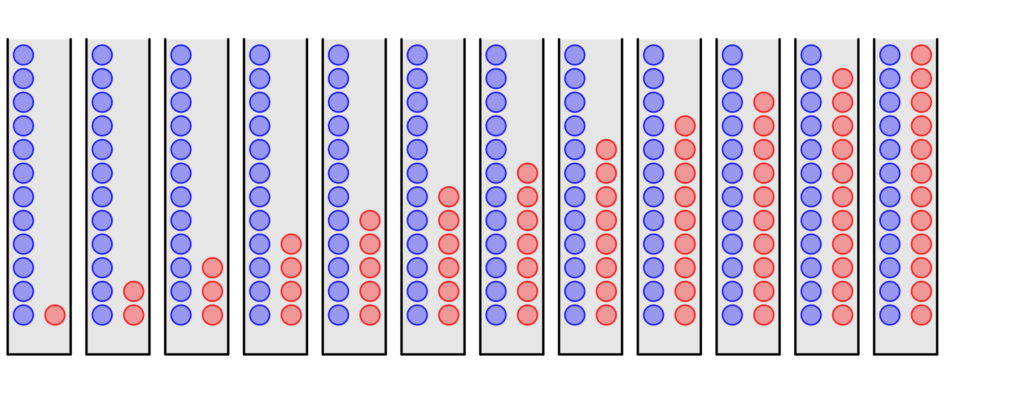
1 – Urnes et boules de couleurs
Étant donné un entier  on dispose de
on dispose de  urnes renfermant chacune des boules de couleurs :
urnes renfermant chacune des boules de couleurs :
- l’urne 1 contient
 boules bleues et 1 boule rouge
boules bleues et 1 boule rouge
- l’urne 2 contient
 boules bleues et 2 boules rouges
boules bleues et 2 boules rouges
- …
- l’une
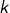 contient
contient  boules bleues et
boules bleues et 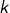 boules rouges
boules rouges
- …
- l’urne
 contient
contient  boules bleues et
boules bleues et  boules rouges
boules rouges
L’illustration ci-dessous montre la configuration pour 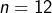 :
:
On envisage alors l’expérience aléatoire suivante. On sélectionne au hasard une urne (les différents choix sont équiprobables) puis, dans cette urne, on tire au hasard une boule (chaque boule présente dans l’urne ayant autant de chances d’être choisie qu’une autre). On note alors 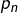 la probabilité que la boule sélectionnée soit rouge.
la probabilité que la boule sélectionnée soit rouge.
On va calculer explicitement 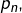 puis préciser sa limite lorsque
puis préciser sa limite lorsque  tend vers
tend vers 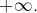
Si l’on note 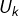 l’évènement « l’urne sélectionnée porte le numéro
l’évènement « l’urne sélectionnée porte le numéro 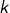 » et
» et 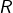 l’évènement « la boule sélectionnée est rouge », alors d’après la formule des probabilités totales :
l’évènement « la boule sélectionnée est rouge », alors d’après la formule des probabilités totales :
![Rendered by QuickLaTeX.com \[p_{n}=\mathbb{P}\left(R\right)=\sum_{k=1}^{n}\mathbb{P}_{U_{k}}\left(R\right)\thinspace\mathbb{P}\left(U_{k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1ea2581d7f858451b04d5532b486e4c8_l3.png)
où
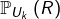
désigne la probabilité conditionnelle de
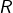
sachant
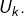
Or, pour tout
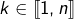
:
![Rendered by QuickLaTeX.com \[\mathbb{P}\left(U_{k}\right)=\dfrac{1}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-874ddd385bdb72a0d2e2666517500f14_l3.png)
et :
![Rendered by QuickLaTeX.com \[\mathbb{P}_{U_{k}}\left(R\right)=\dfrac{k}{n+k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bebd99059ff2339cf3732d0a0efe07a4_l3.png)
Ainsi :
![Rendered by QuickLaTeX.com \[\boxed{p_{n}=\dfrac{1}{n}\sum_{k=1}^{n}\dfrac{k}{n+k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-df207ca4730584a4b710940283aeabb6_l3.png)
que l’on peut écrire sous la forme :
![Rendered by QuickLaTeX.com \[p_{n}=\dfrac{1}{n}\sum_{k=1}^{n}\thinspace f\left(\dfrac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-055ff2217dc1243a3064b78befb6b62f_l3.png)
avec
![Rendered by QuickLaTeX.com f:\left[0,1\right]\rightarrow\mathbb{R},\thinspace t\mapsto\dfrac{t}{1+t}.](https://math-os.com/wp-content/ql-cache/quicklatex.com-8bf4453aa29f164a642889c5e4913fe6_l3.png)
On reconnaît une somme de Riemann pour

et donc :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}p_{n}=\int_{0}^{1}\dfrac{t}{1+t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dc79c3b03d74fcc901ccc4a46e430a9d_l3.png)
Cette dernière intégale se calcule aisément, si l’on remarque que pour tout
![Rendered by QuickLaTeX.com t\in\left[0,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3be682b6dec802a6bc041e84b876fdf4_l3.png)
:
![Rendered by QuickLaTeX.com \[\dfrac{t}{1+t}=1-\dfrac{1}{1+t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-59a4472b2f308fb730e862ee9be9d362_l3.png)
ce qui donne :
![Rendered by QuickLaTeX.com \[\int_{0}^{1}\dfrac{t}{1+t}\thinspace dt=\int_{0}^{1}\left(1-\dfrac{1}{1+t}\right)\thinspace dt=\left[t-\ln\left(1+t\right)\right]_{0}^{1}=1-\ln\left(2\right) \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-59759761e513975336a9f1c5d6607690_l3.png)
Finalement :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\lim_{n\rightarrow+\infty}p_{n}=1-\ln\left(2\right)}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c34f2430d616e7e68cad3c50623cc2b2_l3.png)
Précisons que l’usage du théorème de convergence des sommes de Riemann ne s’imposait pas. En effet, si l’on note 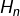 le
le 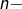 ème nombre harmonique, défini par :
ème nombre harmonique, défini par :
![Rendered by QuickLaTeX.com \[H_{n}=\sum_{k=1}^{n}\dfrac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1b8bbbae3fbf612580193470a1979179_l3.png)
on voit que :
![Rendered by QuickLaTeX.com \[p_{n}=\dfrac{1}{n}\sum_{k=1}^{n}\left(1-\dfrac{n}{n+k}\right)=1-\sum_{k=1}^{n}\dfrac{1}{n+k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e005d930f879dd4ad05bd8dbf38131bf_l3.png)
donc, en ré-indexant cette dernière somme :
![Rendered by QuickLaTeX.com \[p_{n}=1-\sum_{k=n+1}^{2n}\dfrac{1}{k}=1-\left(H_{2n}-H_{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-862e490f933054a0e6f9387126775540_l3.png)
Or, on sait que, lorsque

tend vers
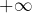
:
![Rendered by QuickLaTeX.com \[H_{n}=\ln\left(n\right)+\gamma+o\left(1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1580070a80fa9df4fb941753aa334a43_l3.png)
où
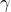
désigne la constante d’Euler. Ainsi :
![Rendered by QuickLaTeX.com \[p_{n}=1-\left(\ln\left(2n\right)+\gamma-\ln\left(n\right)-\gamma+o\left(1\right)\right)=1-\ln\left(2\right)+o\left(1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b0de523b58a093d1daf7bfcf43236e92_l3.png)
On retrouve bien la limite obtenue plus haut. Pour plus d’information sur la constante d’Euler, on pourra consulter cette vidéo :
2 – Une intégrale pas commode
Dans la section précédente, on a essentiellement calculé la limite d’une somme, en détectant qu’il s’agissait d’une somme de Riemann pour une certaine fonction. De nombreux exercices sont construits autour de cette simple idée (« simple » … à condition de savoir ce qu’est une somme de Riemann et aussi de reconnaître, en situation, de quoi il retourne).
Voici quelques exemples de questions de ce type (les réponses sont fournies en annexe) :
Exercice
Calculer les limites des expressions suivantes lorsque l’entier  tend vers
tend vers 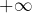 :
:
![Rendered by QuickLaTeX.com \[a_{n}=\dfrac{1}{n^{p+1}}\sum_{k=1}^{n}k^{p}\qquad(p\in\mathbb{N}\text{ est donné})\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-03103223e5183389267741215c246ff4_l3.png)
![Rendered by QuickLaTeX.com \[b_{n}=\sum_{k=1}^{n}\dfrac{1}{\sqrt{n^{2}+k^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b2199f2a9d6b7426a3738726d60bfd47_l3.png)
![Rendered by QuickLaTeX.com \[c_{n}=\dfrac{1}{n^{2}}\left[\prod_{k=1}^{n}\left(n^{2}+k^{2}\right)\right]^{1/n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9756bd92ecd0ea1c7ca153568c82bdef_l3.png)
Cependant, il est parfois possible de faire « l’inverse », c’est-à-dire de calculer la valeur d’une intégrale en passant par des sommes de Riemann.
Par exemple, fixons 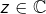 tel que
tel que 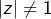 et posons :
et posons :
(1) ![Rendered by QuickLaTeX.com \[J=\int_{0}^{2\pi}\ln\left|z-e^{it}\right|\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6b1bf46c9454ebe06f8f0a623cd2f4ab_l3.png)
L’usage des nombres complexes n’est pas indispensable puisqu’en posant
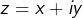
(avec
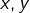
réels) :
![Rendered by QuickLaTeX.com \[z-e^{it}=x-\cos\left(t\right)+i\left(y-\sin\left(t\right)\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7e7f7712061479c913e0f5edf94b8e27_l3.png)
d’où :
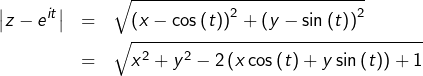
et donc :
(2) ![Rendered by QuickLaTeX.com \[J=\dfrac{1}{2}\int_{0}^{2\pi}\ln\left(x^{2}+y^{2}-2\left(x\cos\left(t\right)+y\sin\left(t\right)\right)+1\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aa4c360adc62cc0512ec88aa1ff097bf_l3.png)
Pour des raisons de concision, on va continuer à exploiter la forme
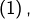
mais que l’on utilise l’une ou l’autre des formes
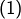
et
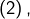
le calcul de l’intégrale ne paraît pas évident ! Pas de primitive qui saute au yeux, pas de possibilité visible de s’en sortir en intégrant par parties ou en changeant de variable … Que faire pour calculer
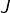
?
Comme annoncé, on va s’en sortir grâce au théorème de convergence des sommes de Riemann. Posons, pour tout 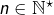 :
:
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{2\pi}{n}\sum_{k=0}^{n-1}\ln\left|z-e^{2ik\pi/n}\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-abe4a6e1a3c43bf0e7a7fbe418cf8fee_l3.png)
qui n’est autre que la
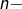
ème somme de Riemann à gauche pour
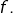
On va trouver une expression plus « sympathique » pour 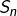 puis en déduire la valeur de
puis en déduire la valeur de 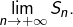
Une somme de logarithmes de réels 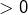 étant égale au logarithme de leurs produits :
étant égale au logarithme de leurs produits :
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{2\pi}{n}\ln\left(\prod_{k=0}^{n-1}\left|z-e^{2ik\pi/n}\right|\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7367707034253abedaf0383943f5e39c_l3.png)
Or, si l’on pose :
![Rendered by QuickLaTeX.com \[P_{n}\left(z\right)=\prod_{k=0}^{n-1}\left(z-e^{2ik\pi/n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-87b47444584074856d0593b9a2aa7844_l3.png)
il est connu que, pour tout
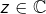
:
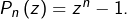
Ainsi :
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{2\pi}{n}\ln\left|z^{n}-1\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-040b43d01d80c75cc866131ec343a031_l3.png)
A présent, on distingue deux cas, selon que le module de
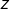
est inférieur ou supérieur à
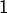
(rappelons que, par hypothèse, ce module est différent de
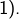
Comme 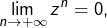 on voit aussitôt que
on voit aussitôt que 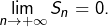
On peut écrire, pour tout 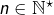 :
:
![Rendered by QuickLaTeX.com \[z^{n}-1=z^{n}\left(1-\dfrac{1}{z^{n}}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-844f91e64022bf016bb4c79a571ca477_l3.png)
d’où :
![Rendered by QuickLaTeX.com \[S_{n}=2\pi\ln\left|z\right|+\dfrac{2\pi}{n}\ln\left|1-\dfrac{1}{z^{n}}\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-94a11275297d2b9fa681042fc542489d_l3.png)
et donc :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}S_{n}=2\pi\ln\left|z\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1097c69dba480da37e23f5355dfe7140_l3.png)
En conclusion :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\int_{0}^{2\pi}\ln\left|z-e^{it}\right|\thinspace dt=\left\{ \begin{array}{cc}0 & \text{si }\left|z\right|<1\\ \\ 2\pi\ln\left|z\right| & \text{si }\left|z\right|>1\end{array}\right.}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1c28f2540d0b1637523dd6bc34eef6e6_l3.png)
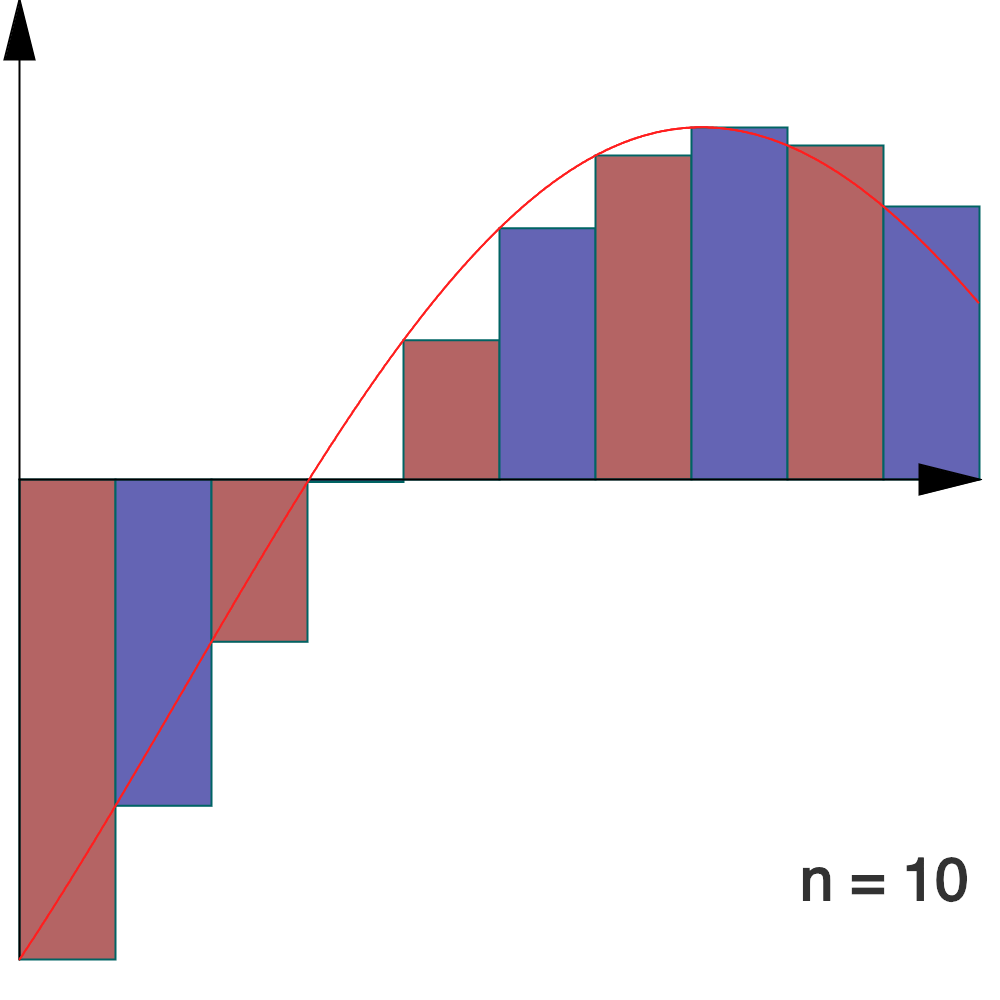
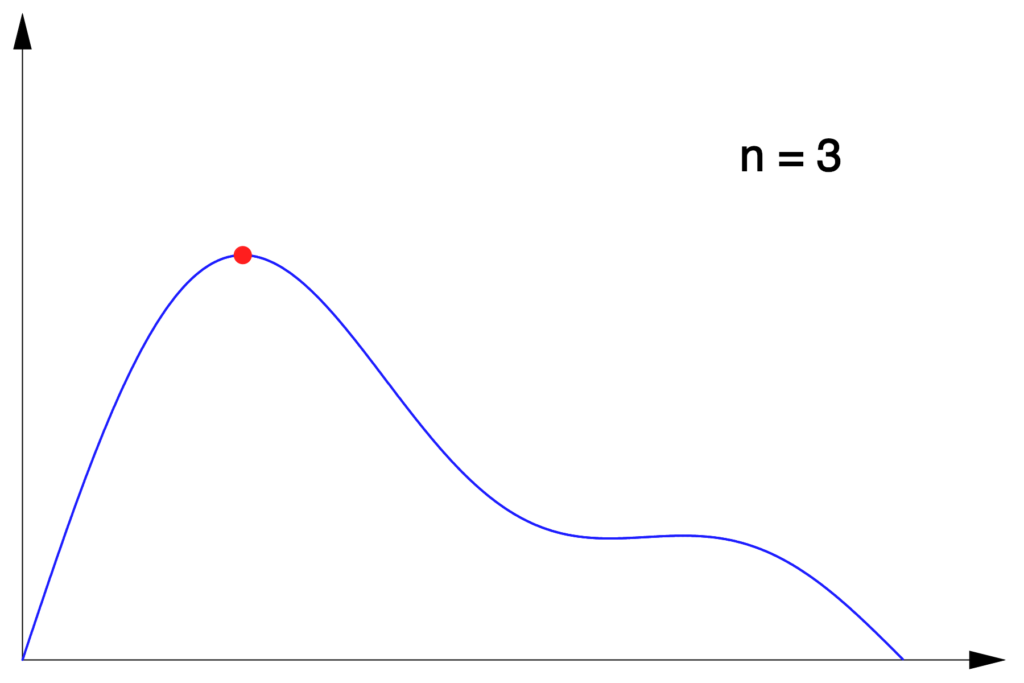
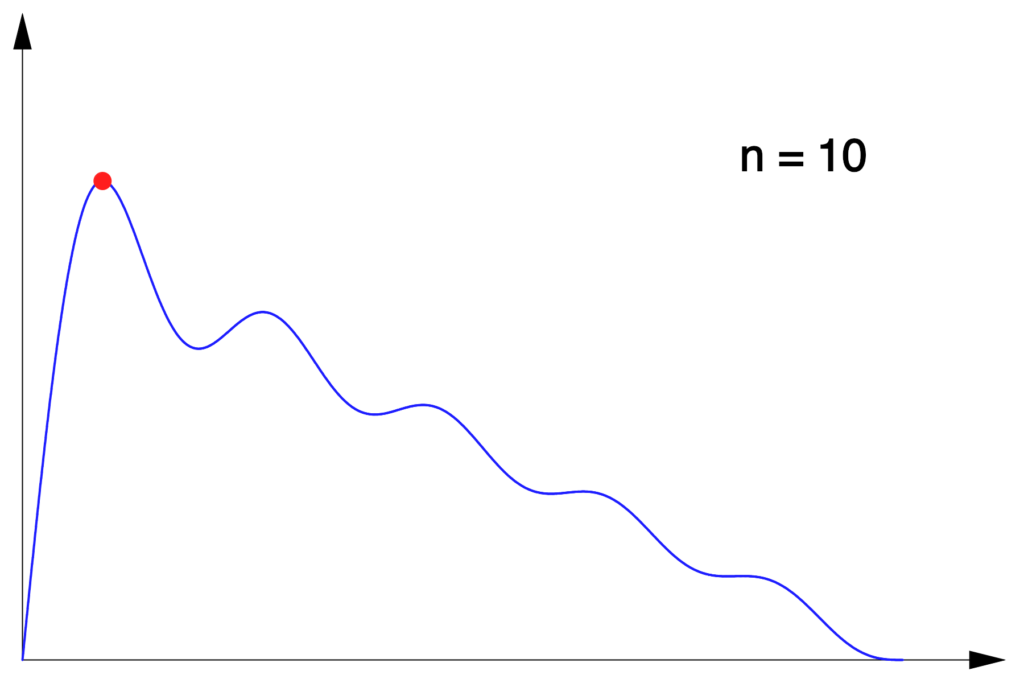
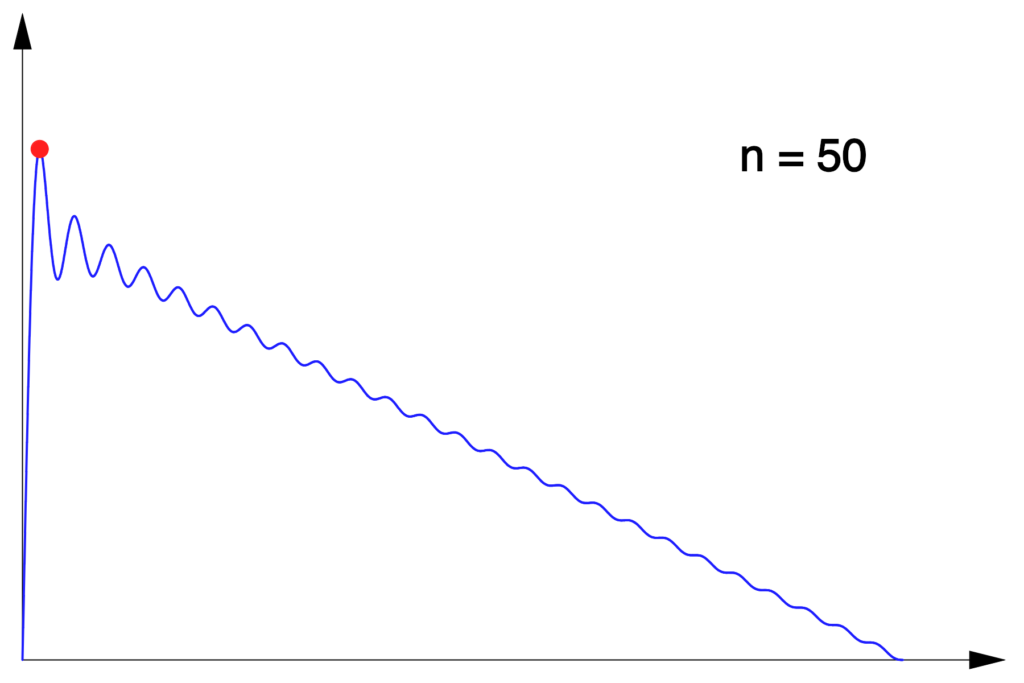
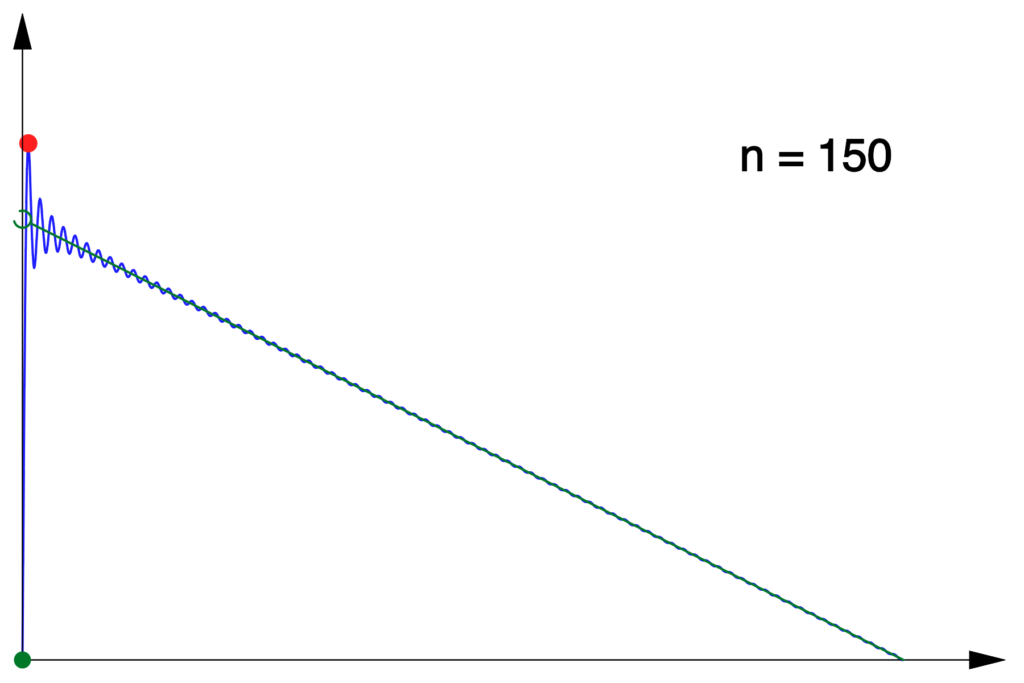
3 – Limite d’un maximum
Considérons, pour tout 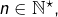 l’application :
l’application :
![Rendered by QuickLaTeX.com \[f_{n}:\left[0,\pi\right]\rightarrow\mathbb{R},\thinspace x\mapsto\sum_{k=1}^{n}\dfrac{\sin\left(kx\right)}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0e730794a3e3438f6cfcefbdc3f453b8_l3.png)
Voici à quoi ressemble son graphe pour quelques valeurs de

:
Dans chaque cas, un petit disque rouge indique le premier maximum local de 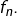
Notons 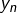 ce maximum et
ce maximum et 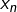 le réel de
le réel de ![Rendered by QuickLaTeX.com \left[0,\pi\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-56e7ca83b44ec07fdd0ba9fe2534ef7f_l3.png) en lequel il est atteint. Une question classique consiste à calculer
en lequel il est atteint. Une question classique consiste à calculer 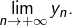
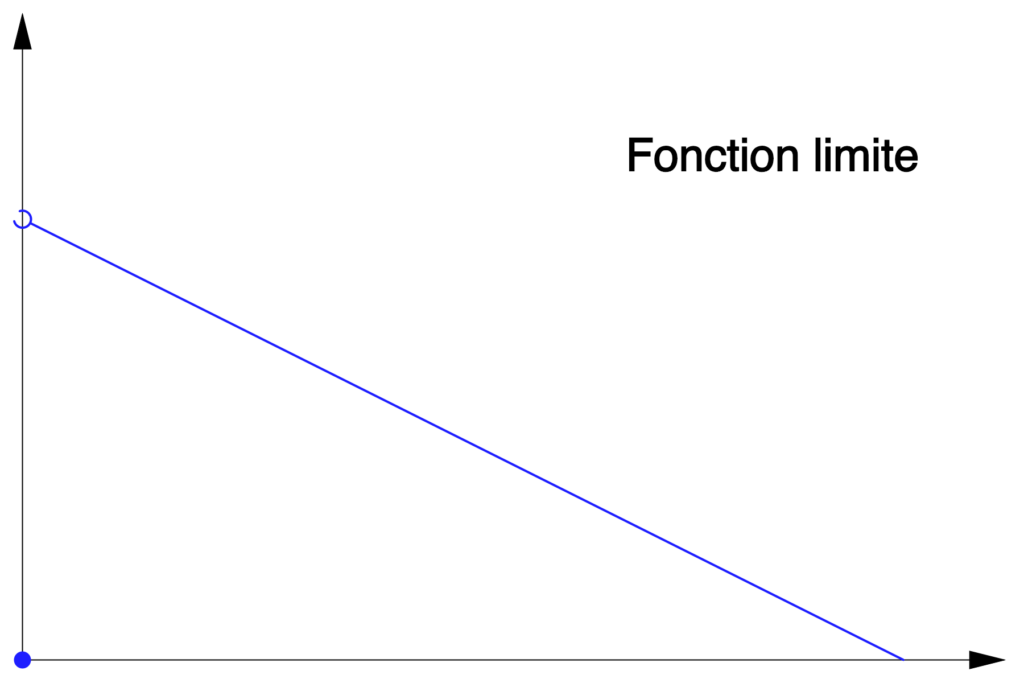
En faisant tendre  vers
vers 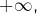 on peut montrer (non détaillé ici) que la suite de fonctions
on peut montrer (non détaillé ici) que la suite de fonctions 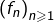 converge simplement vers la fonction discontinue :
converge simplement vers la fonction discontinue :
![Rendered by QuickLaTeX.com \[g:\left[0,\pi\right]\rightarrow\mathbb{R},\thinspace x\mapsto\left\{ \begin{array}{cc}0 & \text{si }x=0\\\\\dfrac{\pi-x}{2} & \text{si }0<x\leqslant\pi\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c36017ffa2da69a6000846b2d49898f8_l3.png)
On pourrait donc s’attendre à ce que la suite 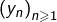 converge vers
converge vers 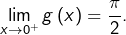 Mais il n’en est rien ! On peut s’en douter en traçant simultanément les graphes de
Mais il n’en est rien ! On peut s’en douter en traçant simultanément les graphes de 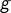 et de
et de 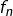 pour un
pour un  « grand » :
« grand » :
Mais alors, si ce n’est pas 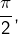 quelle est donc la limite de la suite
quelle est donc la limite de la suite 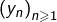 ? Pour élucider cette question, nous allons faire intervenir des … sommes de Riemann (mais je parie que vous vous en doutiez).
? Pour élucider cette question, nous allons faire intervenir des … sommes de Riemann (mais je parie que vous vous en doutiez).
On commence par calculer 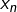 et, pour cela, on s’intéresse au signe de la dérivée de
et, pour cela, on s’intéresse au signe de la dérivée de 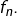 D’après un calcul classique :
D’après un calcul classique :
![Rendered by QuickLaTeX.com \[f_{n}'\left(x\right)=\sum_{k=1}^{n}\cos\left(kx\right)=\text{Re}\left(\sum_{k=1}^{n}e^{ikx}\right)=\dfrac{\sin\left(\dfrac{nx}{2}\right)\cos\left(\left(n+1\right)\dfrac{x}{2}\right)}{\sin\left(\dfrac{x}{2}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dc72951447cc8512aeacc8e940b4522a_l3.png)
et donc
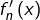
s’annule et change de signe pour les valeurs suivantes de

:
La plus petite de ces valeurs est :
![Rendered by QuickLaTeX.com \[x_{n}=\min\left\{ \dfrac{2\pi}{n},\thinspace\dfrac{\pi}{n+1}\right\} =\dfrac{\pi}{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7ca88c9f3860c21dd8a8e9f07c4c7768_l3.png)
et l’on peut vérifier qu’en ce point,
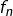
présente un maximum local puisque
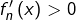
pour
![Rendered by QuickLaTeX.com x\in\left]0,x_{n}\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-1daa9d790757f8259d2b06d5afdc5b36_l3.png)
et
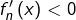
pour
![Rendered by QuickLaTeX.com x\in\left]x_{n},\dfrac{2\pi}{n}\right[.](https://math-os.com/wp-content/ql-cache/quicklatex.com-4aaa737ed626d48cfed98b14199d3947_l3.png)
Par conséquent :
![Rendered by QuickLaTeX.com \[y_{n}=\sum_{k=1}^{n}\dfrac{1}{k}\sin\left(\dfrac{k\pi}{n+1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ea0c8cf4e3263cbd691e39013aa8724b_l3.png)
ou encore :
![Rendered by QuickLaTeX.com \[y_{n}=\frac{\pi}{n+1}\,\sum_{k=0}^{n}\,\frac{\sin\left(\frac{k\pi}{n+1}\right)}{\frac{k\pi}{n+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-755f04c3f4ad18f4fe5bb6232dbce032_l3.png)
L’intérêt de dernière expression est qu’elle fait apparaître une somme de Riemann pour la fonction :
![Rendered by QuickLaTeX.com \[\varphi:\left[0,\pi\right]\rightarrow\mathbb{R},\thinspace x\mapsto\left\{ \begin{array}{cc}\dfrac{\sin\left(x\right)}{x} & \text{si }0<x\leqslant\pi\\\\1 & \text{si }x=0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b9d0e3bc40fc6c9cb46cc055fdc8157e_l3.png)
En conclusion :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\lim_{n\rightarrow+\infty}y_{n}=\int_{0}^{\pi}\dfrac{\sin\left(x\right)}{x}\thinspace dx}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-53b638ea70e9b5b7447033bcc51eeebd_l3.png)
Un calcul approché montre que cette limite est voisine de
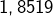
(à
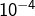
près), une valeur clairement supérieure à
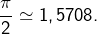
Remarque
Ce résultat, lié à la non uniformité de la convergence de la suite 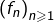 au voisinage de 0, est connu sous le nom de « phénomène de Gibbs ».
au voisinage de 0, est connu sous le nom de « phénomène de Gibbs ».
Plus d’infos à ce sujet sur Wikipedia (en anglais).
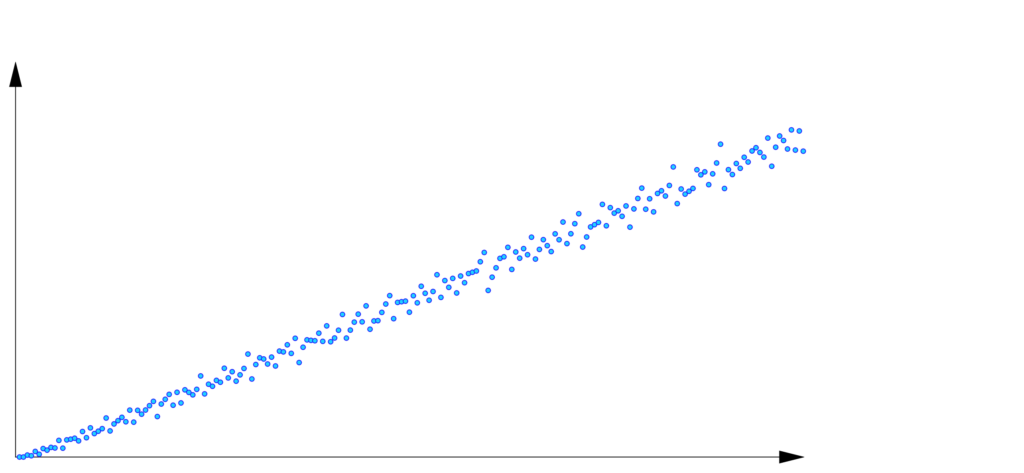
4 – Comportement asymptotique d’une somme
Dans cette section, on s’intéresse à la recherche d’un équivalent, lorsque 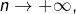 pour la somme :
pour la somme :
![Rendered by QuickLaTeX.com \[G_{n}=\sum_{k=1}^{n}\dfrac{n\mod k}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1ea2c45f25643b78cbf53465bcc3d400_l3.png)
La notation
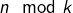
désigne le reste de la division euclidienne de

par
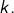
Afin de se faire une idée de la situation, on peut visualiser les premiers termes de la suite 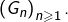 Dans l’illustration ci-dessous, on voit les points de coordonnées
Dans l’illustration ci-dessous, on voit les points de coordonnées 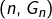 pour
pour 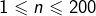 :
:
Cette disposition quasi-linéaire laisse penser qu’il existerait une constante 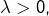 sans doute voisine de
sans doute voisine de 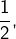 telle que
telle que 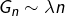 .
.
Comme 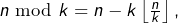 on constate que :
on constate que :
![Rendered by QuickLaTeX.com \[\frac{G_{n}}{n}=\frac{1}{n}\,\sum_{k=1}^{n}\,\left(\frac{n}{k}-\left\lfloor \frac{n}{k}\right\rfloor \right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7fbd4ff04d271b2dd33775ed0784b118_l3.png)
On reconnaît maintenant une somme de Riemann pour :
![Rendered by QuickLaTeX.com \[u:\left]0,1\right]\rightarrow\mathbb{R},\thinspace x\mapsto\dfrac{1}{x}-\left\lfloor \dfrac{1}{x}\right\rfloor\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-974afdb6334ea5d27c9dac417719de7e_l3.png)
qui est intégrable au sens de Riemann sur tout
![Rendered by QuickLaTeX.com \left[a,1\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e0eda7f7908947bc223378f9a5563ac1_l3.png)
(pour
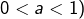
et bornée, donc qu’on peut prolonger (en posant par exemple
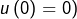
en une application Riemann-intégrable sur
![Rendered by QuickLaTeX.com \left[0,1\right].](https://math-os.com/wp-content/ql-cache/quicklatex.com-c107e9d94bd41831ca96564e1242d487_l3.png)
Ainsi, le théorème s’applique et :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\dfrac{G_{n}}{n}=\int_{0}^{1}\left(\dfrac{1}{x}-\left\lfloor \dfrac{1}{x}\right\rfloor \right)\thinspace dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-929376be6bfbfd6a3ab93b3d63e8d147_l3.png)
Il reste à calculer cette intégrale. Pour cela, il est naturel de calculer
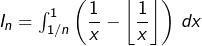
(pour
entier), puis de passer à la limite lorsque

tend vers
Or, pour tout
la relation de Chasles donne :
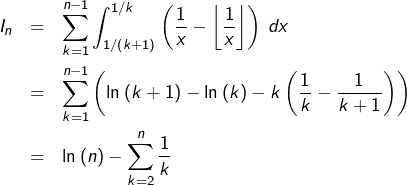
Par ailleurs, comme on l’a rappelé à la
section 1 :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\dfrac{1}{k}=\ln\left(n\right)+\gamma+o\left(1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-59eef8e4316d6bd0756762eefda4c8eb_l3.png)
et donc :
![Rendered by QuickLaTeX.com \[\int_{0}^{1}\left(\dfrac{1}{x}-\left\lfloor \dfrac{1}{x}\right\rfloor \right)\thinspace dx=\lim_{n\rightarrow+\infty}I_{n}=1-\gamma\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c6ca65d03e47fdbc7b9305542617aeda_l3.png)
En conclusion :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{G_{n}\sim\left(1-\gamma\right)n}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-30ece3ab43d7ab3faaf2c372363f1bc9_l3.png)
ce qui démontre la conjecture (avec
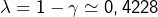
à
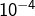
près).
5 – Une inégalité pas très discrète
Etant données deux applications continues ![Rendered by QuickLaTeX.com f,g:\left[a,b\right]\rightarrow\mathbb{R},](https://math-os.com/wp-content/ql-cache/quicklatex.com-7abfd5d955351cdfbeabf9d9f3eaf660_l3.png) on se propose d’établir l’inégalité :
on se propose d’établir l’inégalité :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sqrt{\left(\int_{a}^{b}\,f\left(t\right)\,dt\right)^{2}+\left(\int_{a}^{b}\,g\left(t\right)\,dt\right)^{2}}\leqslant\int_{a}^{b}\,\sqrt{f\left(t\right)^{2}+g\left(t\right)^{2}}\,dt}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0ee12d130e3565c0957f29fddf0dab37_l3.png)
Pour tout
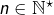
et tout
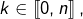
posons :
![Rendered by QuickLaTeX.com \[t_{n,k}=a+\frac{k\left(b-a\right)}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-215650e4220688068ff57816aea51b5b_l3.png)
ainsi que :
![Rendered by QuickLaTeX.com \[S_{n}=\frac{b-a}{n}\,\sum_{k=1}^{n}\,f\left(t_{n,k}\right);\qquad T_{n}=\frac{b-a}{n}\,\sum_{k=1}^{n}\,g\left(t_{n,k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-884c0475f08b8a43d0d3cde1f73dd24a_l3.png)
D’après l’inégalité triangulaire pour la norme euclidienne dans
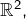
pour tout
uplet

de couples de nombres réels :
![Rendered by QuickLaTeX.com \[\left\Vert \sum_{k=1}^{n}\,\left(x_{k},y_{k}\right)\right\Vert \leqslant\sum_{k=1}^{n}\,\left\Vert \left(x_{k},y_{k}\right)\right\Vert\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ed9d3e28bd0b2e29c00a81fca85ec9eb_l3.png)
c’est-à-dire :
![Rendered by QuickLaTeX.com \[\sqrt{\left(\sum_{k=1}^{n}\,x_{k}\right)^{2}+\left(\sum_{k=1}^{n}\,y_{k}\right)^{2}}\leqslant\sum_{k=1}^{n}\,\sqrt{x_{k}^{2}+y_{k}^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-20126be97286ebbca274c2e80334e106_l3.png)
En remplaçant
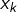
par
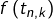
et
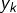
par
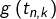
pour chaque
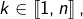
puis en multipliant par
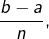
il vient :
![Rendered by QuickLaTeX.com \[\sqrt{\left(S_{n}\right)^{2}+\left(T_{n}\right)^{2}}\leqslant\frac{b-a}{n}\,\sum_{k=1}^{n}\,\sqrt{f\left(t_{n,k}\right)^{2}+g\left(t_{n,k}\right)^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-56875fda51b318fb2e6d0e23a2da82ee_l3.png)
Or, au membre de droite de cette dernière inégalité, on reconnaît une somme de Riemann pour
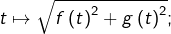
il suffit donc de passer à la limite pour conclure.
Ce calcul donne une illustration de la possibilité d’utiliser des sommes de Riemann pour passer du « discret » au « continu » : pour démontrer un résultat qui concerne des intégrales, on peut essayer d’établir au préalable un résultat analogue pour des sommes, puis passer à la limite. Par exemple, on peut démontrer par ce mécanisme la célèbre inégalité de Jensen pour des intégrales :
Inégalité de Jensen (version intégrale)
Une preuve de ce résultat fait l’objet de l’exercice n° 4 de cette fiche.
Pour revenir à la question initiale, les sommes de Riemann ne constituaient pas un passage obligé. On observe que l’inégalité :
![Rendered by QuickLaTeX.com \[\left(\int_{a}^{b}\,f\right)^{2}+\left(\int_{a}^{b}\,g\right)^{2}\leqslant\left(\int_{a}^{b}\,\sqrt{f^{2}+g^{2}}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-708c9db10626074a48a15007dcd53a72_l3.png)
peut s’écrire, en posant
![Rendered by QuickLaTeX.com \Delta=\left[a,b\right]^{2}](https://math-os.com/wp-content/ql-cache/quicklatex.com-c26209b05978df19c28ff0496ed77a24_l3.png)
:
![Rendered by QuickLaTeX.com \[\iint_{\Delta}\thinspace\left(f(x)f(y)+g(x)g(y)\right)\thinspace dx\thinspace dy\leqslant\iint_{\Delta}\thinspace\sqrt{f^{2}(x)+g^{2}(x)}\sqrt{f^{2}(y)+g^{2}(y)}\thinspace dx\thinspace dy\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3162c986100d6ceac4389387609a196a_l3.png)
Or, pour voir que cette inégalité est vraie, il suffit de montrer que, pour tous réels
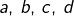
:
![Rendered by QuickLaTeX.com \[ab+cd\leqslant\sqrt{a^{2}+c^{2}}\sqrt{b^{2}+d^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-60f252fe1ceb9417de9f14ce5a72990a_l3.png)
C’est évident si le membre de gauche est négatif. Et sinon, cette inégalité équivaut à :
![Rendered by QuickLaTeX.com \[(ab+cd)^{2}\leqslant(a^{2}+c^{2})(b^{2}+d^{2})\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dd232294ceeeda790e533bbc095fdf85_l3.png)
qui équivaut à son tour à :
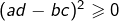
… et qui est donc vraie !
6 – Une question posée à l’oral des ENS
Considérons une application ![Rendered by QuickLaTeX.com f:\left[a,b\right]\rightarrow\mathbb{R}](https://math-os.com/wp-content/ql-cache/quicklatex.com-d4da71c7eb5c9e6aa61c58d77d717be2_l3.png) continue, à valeurs strictement positives.
continue, à valeurs strictement positives.
On demande …
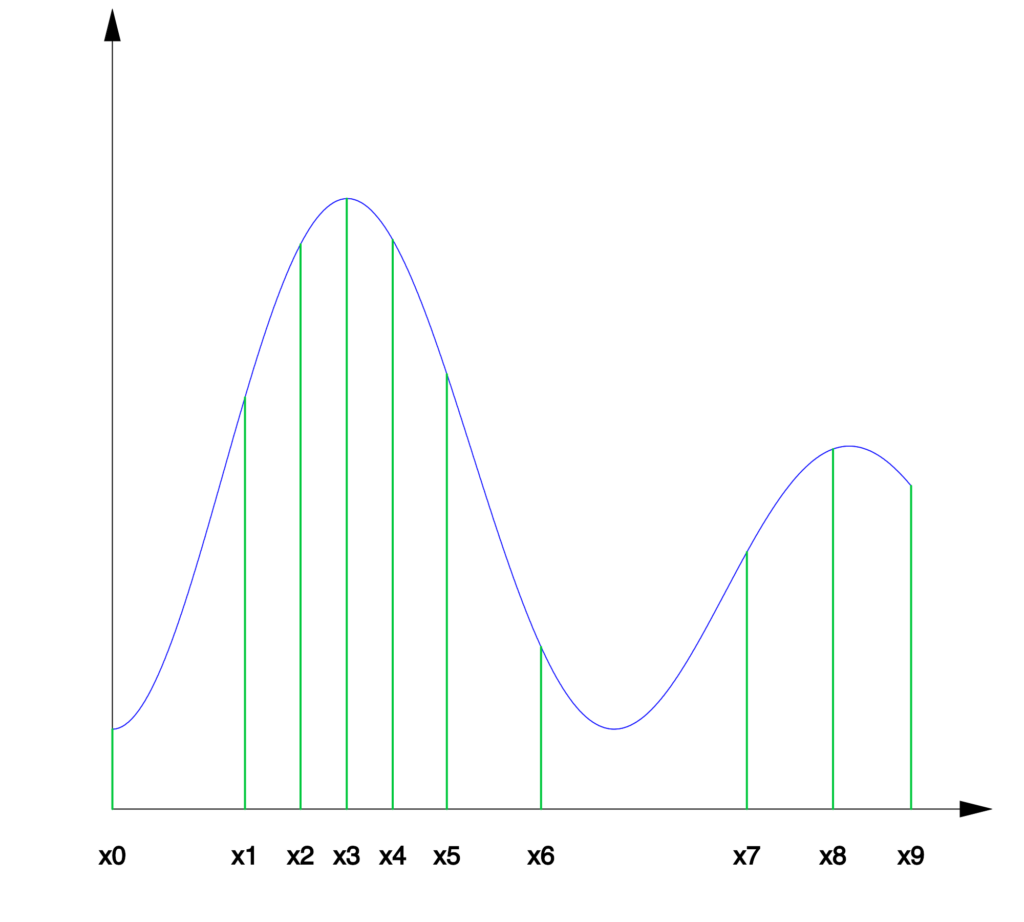
1°) de montrer que, pour tout 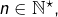 il est possible de former une subdivision
il est possible de former une subdivision 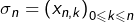 du segment
du segment ![Rendered by QuickLaTeX.com \left[a,b\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-358a945a8ec946c0449cbd1d69dc7a36_l3.png) avec comme toujours :
avec comme toujours :
![Rendered by QuickLaTeX.com \[ a=x_{0,n}<x_{1,n}<\cdots<x_{n-1,n}<x_{n,n}=b\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d88a9864fac05c1662997bccd6b1fad7_l3.png)
mais de telle sorte que l’intégrale de

sur la « tranche numéro
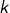
» soit indépendante de
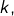
c’est-à-dire :
![Rendered by QuickLaTeX.com \[\forall k\in\left\llbracket 0,n-1\right\rrbracket ,\,\int_{x_{k,n}}^{x_{k+1,n}}\,f\left(t\right)\,dt=\frac{1}{n}\,\int_{a}^{b}\,f\left(t\right)\,dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6200d83f87f2bb77c67c8fc5c12837e7_l3.png)
2°) de calculer :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\,\frac{1}{n}\,\sum_{k=1}^{n}\,f\left(x_{k,n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-041a27cbfa68ead2c4ed081b82ddb1d8_l3.png)
Pour le premier point, introduisons l’application ![Rendered by QuickLaTeX.com F:\left[a,b\right]\rightarrow\mathbb{R},\thinspace x\mapsto\int_{a}^{x}f\left(t\right)\thinspace dt](https://math-os.com/wp-content/ql-cache/quicklatex.com-c04bb9f623b2ee22d9cf2475018c66fc_l3.png) qui est continue (et même de classe
qui est continue (et même de classe 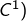 et strictement croissante. De ce fait,
et strictement croissante. De ce fait,  réalise une bijection de
réalise une bijection de ![Rendered by QuickLaTeX.com \left[a,b\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c1c9b62f4ffe493505d6566104a9b311_l3.png) sur
sur ![Rendered by QuickLaTeX.com \left[0,S\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-1a43db17405131a171515889ae6004d1_l3.png) où l’on a posé :
où l’on a posé :
![Rendered by QuickLaTeX.com \[S=\int_{a}^{b}\,f\left(t\right)\,dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-41331b9eac76cca063224c98839901de_l3.png)
Il existe donc, pour chaque
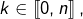
un unique
![Rendered by QuickLaTeX.com x_{k,n}\in\left[a,b\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-62e9394ed3c2350f4e7014f5134e3c7b_l3.png)
tel que :
![Rendered by QuickLaTeX.com \[F\left(x_{k,n}\right)=\frac{kS}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ecf970fb70632ce44ebfc42f58cd1134_l3.png)
On a alors, pour tout
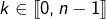
:
![Rendered by QuickLaTeX.com \[\int_{x_{k,n}}^{x_{k+1,n}}\,f\left(t\right)\,dt=F\left(x_{k+1,n}\right)-F\left(x_{k,n}\right)=\frac{S}{n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9b276a54df71380362f4c0421f332b98_l3.png)
comme souhaité. On observe ensuite que :
![Rendered by QuickLaTeX.com \[\frac{1}{n}\,\sum_{k=1}^{n}\,f\left(x_{k,n}\right)=\frac{1}{n}\,\sum_{k=1}^{n}\,f\circ F^{-1}\left(\frac{kS}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f307520160c7ffa3104ab4d5667cc2ff_l3.png)
On reconnaît donc une somme de Riemann pour
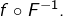
Ainsi :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\frac{1}{n}\,\sum_{k=1}^{n}\,f\left(x_{k,n}\right)=\int_{0}^{1}\,f\circ F^{-1}\left(Sx\right)\,dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3a7131b511fb8065851e8de5c348f5f3_l3.png)
En posant
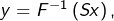
il vient finalement :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\lim_{n\rightarrow+\infty}\,\frac{1}{n}\,\sum_{k=1}^{n}\,f\left(x_{k,n}\right)=\frac{\int_{a}^{b}\,f\left(y\right)^{2}\,dy}{\int_{a}^{b}\,f\left(y\right)\,dy}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3eadd152b98d3aa795308fd6375bf86f_l3.png)
Annexe
Voici les réponses pour les trois limites laissées en suspens au début de la section 2 :
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}a_{n}=\lim_{n\rightarrow+\infty}\dfrac{1}{n}\sum_{k=1}^{n}\left(\dfrac{k}{n}\right)^{p}=\int_{0}^{1}t^{p}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-17220763c7a731aa3d03b8ad4b0e5152_l3.png)
c’est-à-dire :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow+\infty}a_{n}=\dfrac{1}{p+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0364f114b24d0ef3339426d52ad6b1d0_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}b_{n}=\lim_{n\rightarrow+\infty}\dfrac{1}{n}\sum_{k=1}^{n}\dfrac{1}{\sqrt{1+\left(\dfrac{k}{n}\right)^{2}}}=\int_{0}^{1}\dfrac{1}{\sqrt{1+t^{2}}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bc8a7295d0e1b269b719307a3cbb0750_l3.png)
et comme une primitive de
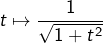
est
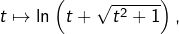
il vient :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow+\infty}b_{n}=\ln\left(1+\sqrt{2}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d8c8ed47a5fc6685798428c2f6312ac3_l3.png)
Enfin :
![Rendered by QuickLaTeX.com \[c_{n}=\left(\dfrac{1}{n^{2n}}\prod_{k=1}^{n}\left(n^{2}+k^{2}\right)\right)^{1/n}=\left(\prod_{k=1}^{n}\left(1+\dfrac{k^{2}}{n^{2}}\right)\right)^{1/n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-be6a7d294c8ea8e7688bae7927ae4817_l3.png)
et donc :
![Rendered by QuickLaTeX.com \[\ln\left(c_{n}\right)=\dfrac{1}{n}\sum_{k=1}^{n}\ln\left(1+\dfrac{k^{2}}{n^{2}}\right)\underset{n\rightarrow+\infty}{\longrightarrow}\int_{0}^{1}\ln\left(1+t^{2}\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-da86f5e0a8eca90b7feef46b97892c4c_l3.png)
En intégrant par parties, on trouve :
![Rendered by QuickLaTeX.com \[\int_{0}^{1}\ln\left(1+t^{2}\right)\thinspace dt=\dfrac{\pi}{2}+\ln\left(2\right)-2\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9a06ef76fffb3fa0ef057fd60da2609c_l3.png)
et donc (par continuité de l’exponentielle) :
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow+\infty}c_{n}=2\thinspace\exp\left(\dfrac{\pi}{2}-2\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-247097a15e5a7a30eef575b455bedf2c_l3.png)
Si cet article vous a intéressé, merci de laisser un petit commentaire 🙂
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{b-a}{n}\sum_{k=1}^{n}f\left(a+\dfrac{k\left(b-a\right)}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d88a99dfa82072b20765767fc1233188_l3.png)
![]()
![Rendered by QuickLaTeX.com \[S'_{n}=\dfrac{b-a}{n}\sum_{k=0}^{n-1}f\left(a+\dfrac{k\left(b-a\right)}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-50f4f924eda56cdb6b4bb2ea56bf561e_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\dfrac{1}{n}\sum_{k=1}^{n}f\left(\dfrac{k}{n}\right)=\int_{0}^{1}f\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fdcd8dd34a85fe6850c7727e80c276d1_l3.png)
 boules bleues et 1 boule rouge
boules bleues et 1 boule rouge boules bleues et 2 boules rouges
boules bleues et 2 boules rouges contient
contient  boules bleues et
boules bleues et  boules rouges
boules rouges contient
contient  boules bleues et
boules bleues et  boules rouges
boules rouges![Rendered by QuickLaTeX.com \[p_{n}=\mathbb{P}\left(R\right)=\sum_{k=1}^{n}\mathbb{P}_{U_{k}}\left(R\right)\thinspace\mathbb{P}\left(U_{k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1ea2581d7f858451b04d5532b486e4c8_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{p_{n}=\dfrac{1}{n}\sum_{k=1}^{n}\dfrac{k}{n+k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-df207ca4730584a4b710940283aeabb6_l3.png)
![Rendered by QuickLaTeX.com \[p_{n}=\dfrac{1}{n}\sum_{k=1}^{n}\thinspace f\left(\dfrac{k}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-055ff2217dc1243a3064b78befb6b62f_l3.png)
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[H_{n}=\sum_{k=1}^{n}\dfrac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1b8bbbae3fbf612580193470a1979179_l3.png)
![Rendered by QuickLaTeX.com \[p_{n}=\dfrac{1}{n}\sum_{k=1}^{n}\left(1-\dfrac{n}{n+k}\right)=1-\sum_{k=1}^{n}\dfrac{1}{n+k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e005d930f879dd4ad05bd8dbf38131bf_l3.png)
![Rendered by QuickLaTeX.com \[p_{n}=1-\sum_{k=n+1}^{2n}\dfrac{1}{k}=1-\left(H_{2n}-H_{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-862e490f933054a0e6f9387126775540_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[a_{n}=\dfrac{1}{n^{p+1}}\sum_{k=1}^{n}k^{p}\qquad(p\in\mathbb{N}\text{ est donné})\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-03103223e5183389267741215c246ff4_l3.png)
![Rendered by QuickLaTeX.com \[b_{n}=\sum_{k=1}^{n}\dfrac{1}{\sqrt{n^{2}+k^{2}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b2199f2a9d6b7426a3738726d60bfd47_l3.png)
![Rendered by QuickLaTeX.com \[c_{n}=\dfrac{1}{n^{2}}\left[\prod_{k=1}^{n}\left(n^{2}+k^{2}\right)\right]^{1/n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9756bd92ecd0ea1c7ca153568c82bdef_l3.png)
![]()
![]()
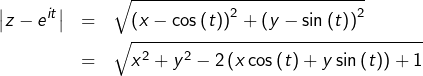
![]()
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{2\pi}{n}\sum_{k=0}^{n-1}\ln\left|z-e^{2ik\pi/n}\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-abe4a6e1a3c43bf0e7a7fbe418cf8fee_l3.png)
![Rendered by QuickLaTeX.com \[S_{n}=\dfrac{2\pi}{n}\ln\left(\prod_{k=0}^{n-1}\left|z-e^{2ik\pi/n}\right|\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7367707034253abedaf0383943f5e39c_l3.png)
![Rendered by QuickLaTeX.com \[P_{n}\left(z\right)=\prod_{k=0}^{n-1}\left(z-e^{2ik\pi/n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-87b47444584074856d0593b9a2aa7844_l3.png)
![]()

![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\int_{0}^{2\pi}\ln\left|z-e^{it}\right|\thinspace dt=\left\{ \begin{array}{cc}0 & \text{si }\left|z\right|<1\\ \\ 2\pi\ln\left|z\right| & \text{si }\left|z\right|>1\end{array}\right.}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1c28f2540d0b1637523dd6bc34eef6e6_l3.png)
![Rendered by QuickLaTeX.com \[f_{n}:\left[0,\pi\right]\rightarrow\mathbb{R},\thinspace x\mapsto\sum_{k=1}^{n}\dfrac{\sin\left(kx\right)}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0e730794a3e3438f6cfcefbdc3f453b8_l3.png)
![Rendered by QuickLaTeX.com \[g:\left[0,\pi\right]\rightarrow\mathbb{R},\thinspace x\mapsto\left\{ \begin{array}{cc}0 & \text{si }x=0\\\\\dfrac{\pi-x}{2} & \text{si }0<x\leqslant\pi\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c36017ffa2da69a6000846b2d49898f8_l3.png)
![Rendered by QuickLaTeX.com \[f_{n}'\left(x\right)=\sum_{k=1}^{n}\cos\left(kx\right)=\text{Re}\left(\sum_{k=1}^{n}e^{ikx}\right)=\dfrac{\sin\left(\dfrac{nx}{2}\right)\cos\left(\left(n+1\right)\dfrac{x}{2}\right)}{\sin\left(\dfrac{x}{2}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dc72951447cc8512aeacc8e940b4522a_l3.png)
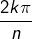 pour
pour 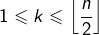
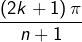 pour
pour 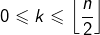
![]()
![Rendered by QuickLaTeX.com \[y_{n}=\sum_{k=1}^{n}\dfrac{1}{k}\sin\left(\dfrac{k\pi}{n+1}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ea0c8cf4e3263cbd691e39013aa8724b_l3.png)
![Rendered by QuickLaTeX.com \[y_{n}=\frac{\pi}{n+1}\,\sum_{k=0}^{n}\,\frac{\sin\left(\frac{k\pi}{n+1}\right)}{\frac{k\pi}{n+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-755f04c3f4ad18f4fe5bb6232dbce032_l3.png)
![Rendered by QuickLaTeX.com \[\varphi:\left[0,\pi\right]\rightarrow\mathbb{R},\thinspace x\mapsto\left\{ \begin{array}{cc}\dfrac{\sin\left(x\right)}{x} & \text{si }0<x\leqslant\pi\\\\1 & \text{si }x=0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b9d0e3bc40fc6c9cb46cc055fdc8157e_l3.png)
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\lim_{n\rightarrow+\infty}y_{n}=\int_{0}^{\pi}\dfrac{\sin\left(x\right)}{x}\thinspace dx}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-53b638ea70e9b5b7447033bcc51eeebd_l3.png)
![Rendered by QuickLaTeX.com \[G_{n}=\sum_{k=1}^{n}\dfrac{n\mod k}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1ea2c45f25643b78cbf53465bcc3d400_l3.png)
![Rendered by QuickLaTeX.com \[\frac{G_{n}}{n}=\frac{1}{n}\,\sum_{k=1}^{n}\,\left(\frac{n}{k}-\left\lfloor \frac{n}{k}\right\rfloor \right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7fbd4ff04d271b2dd33775ed0784b118_l3.png)
![]()
![]()
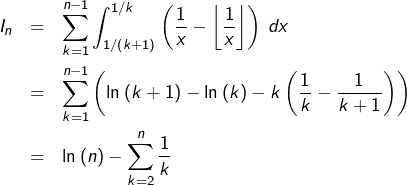
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\dfrac{1}{k}=\ln\left(n\right)+\gamma+o\left(1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-59eef8e4316d6bd0756762eefda4c8eb_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\sqrt{\left(\int_{a}^{b}\,f\left(t\right)\,dt\right)^{2}+\left(\int_{a}^{b}\,g\left(t\right)\,dt\right)^{2}}\leqslant\int_{a}^{b}\,\sqrt{f\left(t\right)^{2}+g\left(t\right)^{2}}\,dt}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0ee12d130e3565c0957f29fddf0dab37_l3.png)
![]()
![Rendered by QuickLaTeX.com \[S_{n}=\frac{b-a}{n}\,\sum_{k=1}^{n}\,f\left(t_{n,k}\right);\qquad T_{n}=\frac{b-a}{n}\,\sum_{k=1}^{n}\,g\left(t_{n,k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-884c0475f08b8a43d0d3cde1f73dd24a_l3.png)
![Rendered by QuickLaTeX.com \[\left\Vert \sum_{k=1}^{n}\,\left(x_{k},y_{k}\right)\right\Vert \leqslant\sum_{k=1}^{n}\,\left\Vert \left(x_{k},y_{k}\right)\right\Vert\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ed9d3e28bd0b2e29c00a81fca85ec9eb_l3.png)
![Rendered by QuickLaTeX.com \[\sqrt{\left(\sum_{k=1}^{n}\,x_{k}\right)^{2}+\left(\sum_{k=1}^{n}\,y_{k}\right)^{2}}\leqslant\sum_{k=1}^{n}\,\sqrt{x_{k}^{2}+y_{k}^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-20126be97286ebbca274c2e80334e106_l3.png)
![Rendered by QuickLaTeX.com \[\sqrt{\left(S_{n}\right)^{2}+\left(T_{n}\right)^{2}}\leqslant\frac{b-a}{n}\,\sum_{k=1}^{n}\,\sqrt{f\left(t_{n,k}\right)^{2}+g\left(t_{n,k}\right)^{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-56875fda51b318fb2e6d0e23a2da82ee_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\left(\int_{a}^{b}\,f\right)^{2}+\left(\int_{a}^{b}\,g\right)^{2}\leqslant\left(\int_{a}^{b}\,\sqrt{f^{2}+g^{2}}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-708c9db10626074a48a15007dcd53a72_l3.png)
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\forall k\in\left\llbracket 0,n-1\right\rrbracket ,\,\int_{x_{k,n}}^{x_{k+1,n}}\,f\left(t\right)\,dt=\frac{1}{n}\,\int_{a}^{b}\,f\left(t\right)\,dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6200d83f87f2bb77c67c8fc5c12837e7_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\,\frac{1}{n}\,\sum_{k=1}^{n}\,f\left(x_{k,n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-041a27cbfa68ead2c4ed081b82ddb1d8_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\frac{1}{n}\,\sum_{k=1}^{n}\,f\left(x_{k,n}\right)=\frac{1}{n}\,\sum_{k=1}^{n}\,f\circ F^{-1}\left(\frac{kS}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f307520160c7ffa3104ab4d5667cc2ff_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}\frac{1}{n}\,\sum_{k=1}^{n}\,f\left(x_{k,n}\right)=\int_{0}^{1}\,f\circ F^{-1}\left(Sx\right)\,dx\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3a7131b511fb8065851e8de5c348f5f3_l3.png)
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\lim_{n\rightarrow+\infty}\,\frac{1}{n}\,\sum_{k=1}^{n}\,f\left(x_{k,n}\right)=\frac{\int_{a}^{b}\,f\left(y\right)^{2}\,dy}{\int_{a}^{b}\,f\left(y\right)\,dy}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3eadd152b98d3aa795308fd6375bf86f_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}a_{n}=\lim_{n\rightarrow+\infty}\dfrac{1}{n}\sum_{k=1}^{n}\left(\dfrac{k}{n}\right)^{p}=\int_{0}^{1}t^{p}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-17220763c7a731aa3d03b8ad4b0e5152_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\lim_{n\rightarrow+\infty}a_{n}=\dfrac{1}{p+1}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0364f114b24d0ef3339426d52ad6b1d0_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow+\infty}b_{n}=\lim_{n\rightarrow+\infty}\dfrac{1}{n}\sum_{k=1}^{n}\dfrac{1}{\sqrt{1+\left(\dfrac{k}{n}\right)^{2}}}=\int_{0}^{1}\dfrac{1}{\sqrt{1+t^{2}}}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bc8a7295d0e1b269b719307a3cbb0750_l3.png)
![]()
![Rendered by QuickLaTeX.com \[c_{n}=\left(\dfrac{1}{n^{2n}}\prod_{k=1}^{n}\left(n^{2}+k^{2}\right)\right)^{1/n}=\left(\prod_{k=1}^{n}\left(1+\dfrac{k^{2}}{n^{2}}\right)\right)^{1/n}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-be6a7d294c8ea8e7688bae7927ae4817_l3.png)
![Rendered by QuickLaTeX.com \[\ln\left(c_{n}\right)=\dfrac{1}{n}\sum_{k=1}^{n}\ln\left(1+\dfrac{k^{2}}{n^{2}}\right)\underset{n\rightarrow+\infty}{\longrightarrow}\int_{0}^{1}\ln\left(1+t^{2}\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-da86f5e0a8eca90b7feef46b97892c4c_l3.png)
![]()
![]()



seems very interesting, scanned through it, will study it. Thank you!
de errard.serge
tres bonne idée;bien construit