Le lemme d’évasion

On définit une suite \left(z_{n}\right)\in\mathbb{C}^{\mathbb{N}} en choisissant deux nombres complexes s et c et en posant :

    \[z_{0}=s\qquad\text{et}\qquad\forall n\in\mathbb{N},\thinspace z_{n+1}=z_{n}^{2}+c\]

On note K_{c}=\left\{ s\in\mathbb{C};\thinspace\left(z_{n}\right)\text{ est bornée}\right\} . C’est « l’ensemble de Julia rempli ».

L’ensemble de Mandelbrot M est défini comme l’ensemble des c\in\mathbb{C} pour lesquels K_c est connexe. On sait depuis les travaux de Pierre Fatou et Gaston Julia (un peu avant 1920) que :

    \[M=\{c\in\mathbb{C};\,0\in K_c\}\]

Remarque

Ce qu’on appelle l’ensemble de Julia (tout court) est la frontière de K_{c}.

Le lemme d’évasion

Lemme

S’il existe p\in\mathbb{N} tel que \left|z_{p}\right|>\max\left\{ 2,\thinspace\left|c\right|\right\} alors s\notin K_{c}.

On pose \epsilon=\left|z_{p}\right|-2>0 et l’on prouve par récurrence que :

(\star)   \[\forall n\geqslant p,\thinspace\left|z_{n}\right|\geqslant\left(1+\epsilon\right)^{n-p}\left|z_{p}\right|\]

Cette inégalité est vraie pour n=p. Supposons-la vraie pour un certain n\geqslant p; alors :

    \[\left|z_{n+1}\right|=\left|z_{n}^{2}+c\right|\geqslant\left|z_{n}\right|^{2}-\left|c\right|\geqslant\left|z_{n}\right|^{2}-\left|z_{n}\right|=\left|z_{n}\right|\left(\left|z_{n}\right|-1\right)=\left|z_{n}\right|\left(\left(\left|z_{n}\right|-2\right)+1\right)\]

Or \left|z_{n}\right|-2>\epsilon et donc \left|z_{n+1}\right|\geqslant\left(1+\epsilon\right)\left|z_{n}\right|, d’où grâce à l’hypothèse de récurrence :

    \[\left|z_{n+1}\right|\geqslant\left(1+\epsilon\right)^{n+1-p}\left|z_{p}\right|\]

comme souhaité. La relation \left(\star\right) montre en particulier que {\displaystyle \lim_{n\rightarrow+\infty}\left|z_{n}\right|=+\infty} et donc que s\notin K_{c}.

Corollaire

Si \left|c\right|>2, alors 0\notin K_{c}.

En effet, en prenant s=0 comme point de départ de l’itération, on voit que z_{2}=c^{2}+c et donc \left|z_{2}\right|=\left|c\right|\thinspace\left|c+1\right|. Or 2<\left|\left(c+1\right)-1\right|\leqslant\left|c+1\right|+1, d’où \left|c+1\right|>1 et, par conséquent : \left|z_{2}\right|>\left|c\right|>2. Il ne reste plus qu’à invoquer le lemme d’évasion.

Remarque

D’après ce corollaire, l’ensemble de Mandelbrot est contenu dans le disque fermé de centre 0 est de rayon 2.

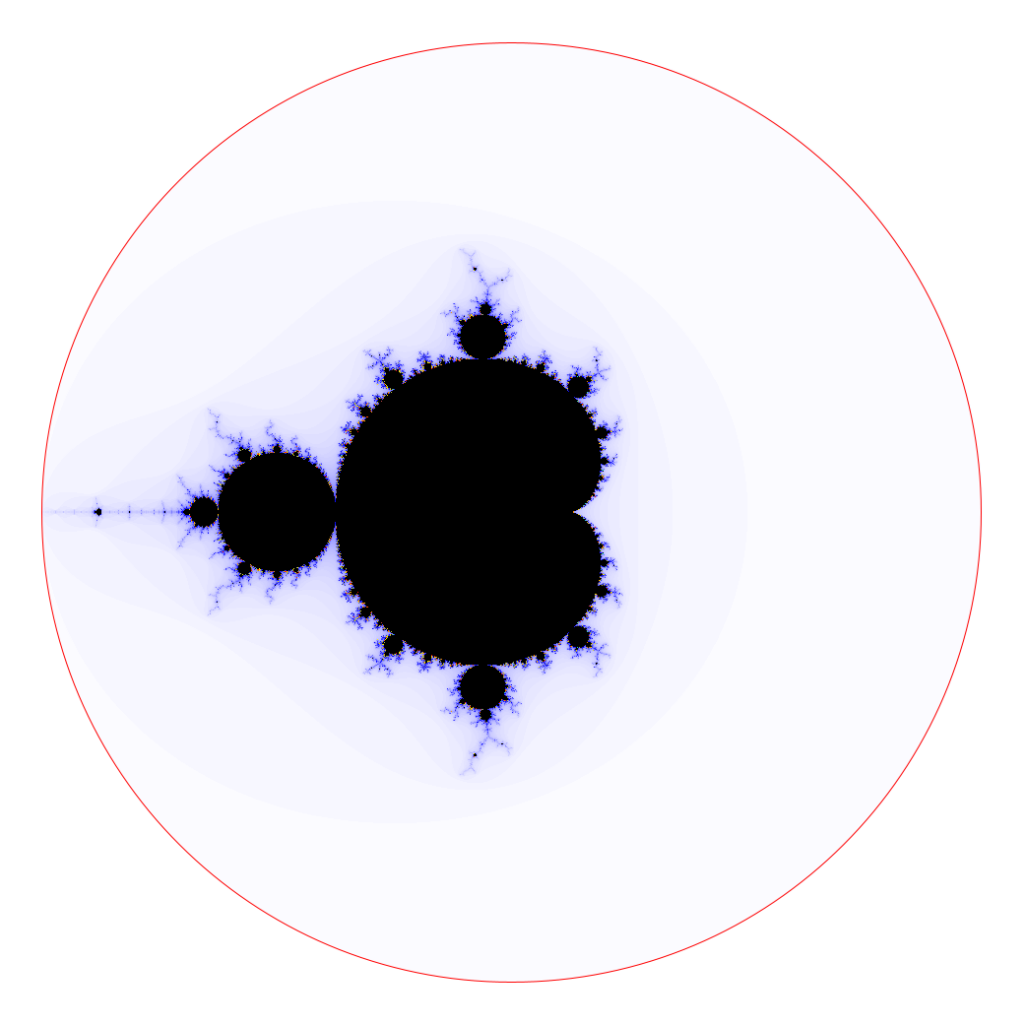
Compacité des ensembles de Julia remplis

Proposition

Pour tout c\in\mathbb{C}, l’ensemble K_{c} est compact et globalement invariant par f_{c}:z\mapsto z^{2}+c.

Posons R=\max\left\{ 2,\left|c\right|\right\} . La contraposée de l’implication établie dans le lemme d’évasion dit que si s\in K_{c}, alors \forall n\in\mathbb{N},\thinspace\left|z_{n}\right|\leqslant R et en particulier \left|s\right|=\left|z_{0}\right|\leqslant R. Ainsi : K_{c}\subset\overline{D}\left(0,R\right) donc K_{c} est borné.

La réciproque est évidente : si \forall n\in\mathbb{N},\thinspace\left|z_{n}\right|\leqslant R, alors la suite \left(z_{n}\right) est borné donc s\in K_{c}. Bref :

(\star\star)   \[s\in K_{c}\Leftrightarrow\forall n\in\mathbb{N},\thinspace\left|z_{n}\right|\leqslant R\]

Il en résulte que :

    \[K_{c}=\bigcap_{n\geqslant0}P_{n,c}^{-1}\left\langle \overline{D}\left(0,R\right)\right\rangle\]

où P_{n,c} désigne la n-ème itérée de f_{c}. Donc K_{c} est fermé (intersection d’une famille de fermés).

Ainsi, K_{c} est compact en tant que partie fermée et bornée de \mathbb{C}.

Maintenant, si s\in K_{c} et si \zeta désigne un antécédent de s par f_{c}, alors la suite qui démarre à s étant bornée, il en va de même de celle qui démarre à \zeta et donc \zeta\in K_{c}. Donc K_{c}\subset f_{c}\left\langle K_{c}\right\rangle . Inversement, si s\in f_{c}\left\langle K_{c}\right\rangle , alors il existe \zeta\in K_{c} tel que s=f_{c}\left(\zeta\right); la suite qui démarre à \zeta est bornée et donc celle qui démarre à s aussi (c’est la même, privée de son premier terme). Donc f_{c}\left\langle K_{c}\right\rangle \subset K_{c}.

Avec des arguments similaires, on voit que f_{c}^{-1}\left\langle K_{c}\right\rangle =K_{c}. Finalement :

    \[\boxed{f_{c}^{-1}\left\langle K_{c}\right\rangle =K_{c}=f_{c}\left\langle K_{c}\right\rangle }\]

Remarque

Attention aux généralisations hâtives … Si \varphi:X\rightarrow X et A\subset X, le fait que \varphi\left\langle X\right\rangle =X n’entraîne pas que \varphi^{-1}\left\langle X\right\rangle =X. Contre-exemple avec \varphi:\mathbb{R}\rightarrow\mathbb{R},\thinspace x\mapsto x^{2} et A=\left[0,1\right]. On a en effet \varphi\left\langle \left[0,1\right]\right\rangle =\left[0,1\right] mais \varphi^{-1}\left\langle \left[0,1\right]\right\rangle =\left[-1,1\right].

Compacité de l’ensemble de Mandelbrot

Proposition

L’ensemble de Mandelbrot est compact.

Considérons la suite de polynôme \left(Q_{k}\right)_{k\geqslant0} définie par :

    \[Q_{0}=0\qquad\text{et}\qquad\forall k\in\mathbb{N},\thinspace Q_{k+1}=Q_{k}^{2}+X\]

Grâce au lemme d’évasion et son corollaire, on sait que :

    \[M=\left\{ c\in\mathbb{C};\thinspace\forall n\in\mathbb{N}^{\star},\thinspace\left|Q_{n}\left(c\right)\right|\leqslant2\right\}\]

Autrement dit, en posant K_{n}=Q_{n}^{-1}\left\langle \overline{D}\left(0,2\right)\right\rangle :

    \[M=\bigcap_{n\geqslant1}K_{n}\]

Pour tout n\geqslant1, Q_{n} est continue (polynôme !), donc K_{n} est fermé (image réciproque du fermé \overline{D}\left(0,2\right) par une application continue). Par conséquent, M est fermé (intersection de fermés). De plus, M est borné puisque contenu dans K_{1}=\overline{D}\left(0,2\right) (mais on le sait depuis le corollaire …) et donc M est compact.

Proposition

La suite \left(K_{n}\right)_{n\geqslant1} est décroissante (pour l’inclusion).

Si \left|z\right|>2 alors, par récurrence :

    \[\forall n\in\mathbb{N}^{\star},\thinspace\left|Q_{n}\left(z\right)\right|\geqslant\left|z\right|^{2}-\left|z\right|\]

En effet, pour n=1 :

    \[\left|Q_{1}\left(z\right)\right|=\left|z^{2}+z\right|\geqslant\left|\left|z\right|^{2}-\left|z\right|\right|=\left|z\right|^{2}-\left|z\right|\]

Puis, si \left|Q_{n}\left(z\right)\right|>\left|z\right|^{2}-\left|z\right| pour un certain n\geqslant1, alors :

    \begin{eqnarray*}\left|Q_{n+1}\left(z\right)\right| & = & \left|Q_{n}\left(z\right)^{2}+z\right|\\& \geqslant & \left|Q_{n}\left(z\right)\right|^{2}-\left|z\right|\\& \geqslant & \left(\left|z\right|^{2}-\left|z\right|\right)^{2}-\left|z\right|\\& = & \left|z\right|^{3}\left(\left|z\right|-2\right)+\left|z\right|^{2}-\left|z\right|\\& \geqslant & \left|z\right|^{2}-\left|z\right|\end{eqnarray*}

comme souhaité. A fortiori :

(\heartsuit)   \[\boxed{\left|z\right|>2\Rightarrow\forall n\in\mathbb{N}^{\star},\thinspace\left|Q_{n}\left(z\right)\right|>2}\]

Maintenant, si \left|Q_{n+1}\left(z\right)\right|\leqslant2 alors \left|z\right|\leqslant2 d’après \left(\heartsuit\right), et donc :

    \[\left|Q_{n}\left(z\right)\right|^{2}=\left|Q_{n+1}\left(z\right)-z\right|\leqslant\left|Q_{n+1}\left(z\right)\right|+\left|z\right|\leqslant4\]

d’où \left|Q_{n}\left(z\right)\right|\leqslant2. Ceci prouve que K_{n+1}\subset K_{n}.

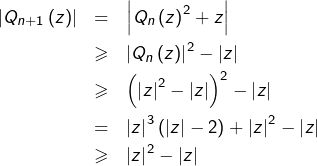
Remarque

Si l’on montrait la connexité de chaque K_{n} (ce qui est vrai, mais pas commode …) il en résulterait que M est connexe, au titre d’intersection d’une suite décroissante de compacts connexes.

Ci-dessous, on a dessiné K_{n} pour 1\leqslant n\leqslant6. On voit bien la décroissance et l’on devine la présence de M à la limite :

La connexité de M a été prouvé par A. Douady et L.H. Hubbard en 1984 (par des techniques sophistiquées d’analyse complexe).

Si cet article vous a intéressé, merci de laisser un petit commentaire 🙂

Partager cet article
    
Étiquettes : , , , , , , , , , , , , , ,

Cet article a 2 commentaires

  1. Jean-Paul Truc 12 Oct 2025 Répondre

    Un article clair et bien structuré !

    1. René Adad 12 Oct 2025 Répondre

      Merci Jean-Paul 🙂

Laisser un commentaire