Dans cet article, on examine les liens entre continuité, injectivité et monotonie, pour une application 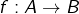 où
où 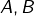 sont deux parties de
sont deux parties de 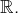
Le principal résultat est le théorème suivant, démontré à la section 2:
Les notions d’injectivité, de monotonie et de continuité sont supposées connues, mais par précaution, les définitions associées sont rappelées en annexe.
Ne sachant pas si ce théorème est attribué à un(e) mathématicien(ne) en particulier, je propose d’adopter le sigle CISM pour « Continue et Injective implique Strictement Monotone »… Si vous avez connaissance d’une dénomination plus officielle, merci de l’indiquer en commentaire.
1 – Observations Préalables
La continuité n’implique évidemment ni l’injectivité, ni la monotonie ! Penser à 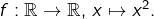
L’exemple de 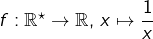 prouve que l’injectivité n’implique pas la monotonie. Et si l’on rajoute la continuité, ce n’est pas mieux … avec le même exemple ! (eh oui, le fonction inverse est continue sur
prouve que l’injectivité n’implique pas la monotonie. Et si l’on rajoute la continuité, ce n’est pas mieux … avec le même exemple ! (eh oui, le fonction inverse est continue sur 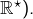 Cependant, si l’ensemble de départ est un intervalle (ce qui n’est pas le cas de
Cependant, si l’ensemble de départ est un intervalle (ce qui n’est pas le cas de 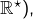 alors l’hypothèse injectivité + monotonie entraîne la stricte monotonie : voir section 2.
alors l’hypothèse injectivité + monotonie entraîne la stricte monotonie : voir section 2.
Ajoutons qu’une application définie sur un intervalle, qui est injective mais discontinue, n’a aucune raison d’être strictement monotone. Exemple :
![Rendered by QuickLaTeX.com \[[0,1[\rightarrow\mathbb{R},\,x\mapsto\left\{\begin{array}{cc}x+\frac12 & \text{si }0\leqslant x\leqslant\frac12\\\\x-\frac12 & \text{si }\frac12<x<1\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-412510084e2e6718cbcb7854fb2a1605_l3.png)
Enfin, il est évident que la stricte monotonie implique l’injectivité. Evident … à condition de considérer qu’on a affaire à une application 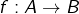 où
où 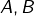 sont des parties de
sont des parties de  ou, plus généralement, d’un ensemble totalement ordonné. Pour des ensembles partiellement ordonnés, ce n’est plus vrai en général. Par exemple, si l’on note
ou, plus généralement, d’un ensemble totalement ordonné. Pour des ensembles partiellement ordonnés, ce n’est plus vrai en général. Par exemple, si l’on note 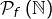 l’ensemble de parties finies de
l’ensemble de parties finies de 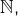 alors l’application
alors l’application 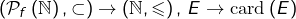 est strictement croissante mais non injective.
est strictement croissante mais non injective.
2 – Le theorème CISM
Ce théorème a été énoncé dans le préambule.
On en donne ici deux preuves (la seconde, plus concise, utilise un bagage théorique un peu plus épais; la première est celle que j’utilise dans mon cours de MPSI).
Preuve 1
Soient 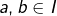 tels que
tels que 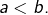 Comme
Comme  est injective,
est injective, 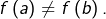 Supposons par exemple que
Supposons par exemple que 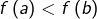 et montrons que
et montrons que  est strictement croissante. Pour cela, considérons
est strictement croissante. Pour cela, considérons 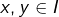 tels que
tels que 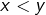 et introduisons l’application
et introduisons l’application
![Rendered by QuickLaTeX.com \[\varphi:\left[0,1\right]\rightarrow\mathbb{R},\thinspace t\mapsto f\left(\left(1-t\right)a+tx\right)-f\left(\left(1-t\right)b+ty\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f0d910d54b3514a778d5ee5af74118ff_l3.png)
Tout d’abord,
est bien définie car, pour tout
![Rendered by QuickLaTeX.com t\in\left[0,1\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-d719a2b3e7348ff815735e1ec4ebcbaf_l3.png)
les réels
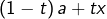
et
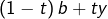
appartiennent à l’intervalle
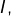
ce qui permet de leur appliquer
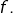
L’intérêt de cette application 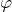 est qu’elle permet de formaliser l’idée d’une « déformation continue » de la différence
est qu’elle permet de formaliser l’idée d’une « déformation continue » de la différence 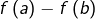 vers la différence
vers la différence 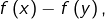 le signe de cette différence restant inchangé tout au long de la déformation.
le signe de cette différence restant inchangé tout au long de la déformation.
Ce n’est pas clair ? Détaillons …
Comme 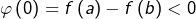 et
et 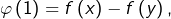 si l’on prouve que
si l’on prouve que 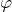 est de signe constant, il en résultera que
est de signe constant, il en résultera que 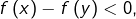 ce qui est exactement la conclusion visée.
ce qui est exactement la conclusion visée.
Comme 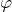 est continue (ce qui résulte de la continuité de
est continue (ce qui résulte de la continuité de 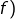 sur l’intervalle
sur l’intervalle 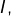 si
si 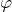 n’était pas de signe constant, elle s’annulerait (d’après le théorème des valeurs intermédiaires). Il existerait donc
n’était pas de signe constant, elle s’annulerait (d’après le théorème des valeurs intermédiaires). Il existerait donc ![Rendered by QuickLaTeX.com t\in\left]0,1\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-f16ef91e6b49c78a44d1607f7ebabd97_l3.png) tel que
tel que 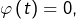 d’où d’après l’injectivité de
d’où d’après l’injectivité de  :
:
![Rendered by QuickLaTeX.com \[\left(1-t\right)a+tx=\left(1-t\right)b+ty\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-26afd8a82dfe91a3d3482e1f60668f0f_l3.png)
c’est-à-dire :
![Rendered by QuickLaTeX.com \[\left(1-t\right)\left(a-b\right)=t\left(y-x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-25001385df7347a06c91265d54070f98_l3.png)
Mais une telle égalité est impossible puisque le membre de gauche est strictement négatif, tandis que celui de droite est strictement positif. On vient de montrer par l’absurde que
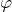
est de signe constant, comme annoncé.
Bien entendu, nous si nous avions supposé en début de preuve que  alors le raisonnement précédent appliqué à
alors le raisonnement précédent appliqué à 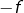 prouverait que
prouverait que  est strictement décroissante. Bref,
est strictement décroissante. Bref,  est strictement monotone.
est strictement monotone.
Preuve 2
Posons 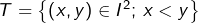 et considérons l’application
et considérons l’application
![Rendered by QuickLaTeX.com \[u:T\rightarrow\mathbb{R},\thinspace\left(x,y\right)\mapsto f\left(x\right)-f\left(y\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-cb94bc692960776a9ef87370482b86b7_l3.png)
Comme

est continue, alors

est aussi continue. Par ailleurs,
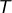
est (convexe donc) connexe et donc
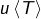
est une partie connexe de
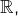
autrement dit un intervalle. Mais comme

est injective,

ne s’annule pas et donc
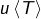
est inclus dans
![Rendered by QuickLaTeX.com \left]-\infty,0\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-96cffb96d97afa19bd62834dd5bc71a5_l3.png)
ou bien dans
![Rendered by QuickLaTeX.com \left]0,+\infty\right[.](https://math-os.com/wp-content/ql-cache/quicklatex.com-efeb3c1fa9cce64a033b154c182e29fe_l3.png)
Ceci prouve que

est strictement monotone (strictement croissante si
![Rendered by QuickLaTeX.com u\left\langle T\right\rangle \subset\left]-\infty,0\right[,](https://math-os.com/wp-content/ql-cache/quicklatex.com-8ddb766ad3c75f51392ba862b64cf2dc_l3.png)
strictement décroissante si
![Rendered by QuickLaTeX.com u\left\langle T\right\rangle \subset\left]0,+\infty\right[).](https://math-os.com/wp-content/ql-cache/quicklatex.com-47b70bdd103cea3ef316df0748be4812_l3.png)
Passons à des applications du théorème CISM.
3 – Une extension du théorème de Rolle
Le résultat suivant est bien connu :
Légèrement moins classique et faisant souvent l’objet d’un exercice :
Extension du théorème de Rolle à un intervalle non borné
On peut démontrer ceci en considérant l’application
![Rendered by QuickLaTeX.com \[\theta:\left[0,1\right[\rightarrow\left[a,+\infty\right[,\thinspace t\mapsto a+\dfrac{t}{1-t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6e13419851bfeccddc85b1462e18bd16_l3.png)
et en remarquant que
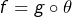
est prolongeable en une application continue sur
![Rendered by QuickLaTeX.com \left[0,1\right],](https://math-os.com/wp-content/ql-cache/quicklatex.com-b01ef9f1983c969ecb0687222e635278_l3.png)
qui vérifie les hypothèses du théorème de Rolle. Il existe donc
![Rendered by QuickLaTeX.com c\in\left]0,1\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-92100b32e6a1ba9214e3a16a9b645536_l3.png)
tel que
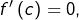
c’est-à-dire
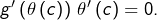
Mais comme
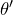
ne s’annule pas, on obtient la conclusion en posant
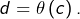
Autre point de vue : on observe que 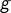 ne peut pas être injective. En effet, si
ne peut pas être injective. En effet, si 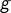 était injective, elle serait strictement monotone (d’après le théorème CISM) mais ceci est incompatible avec le fait que
était injective, elle serait strictement monotone (d’après le théorème CISM) mais ceci est incompatible avec le fait que 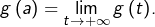 Par conséquent, il existe
Par conséquent, il existe 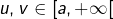 tels que
tels que 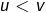 et
et 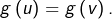 Il suffit alors d’appliquer le théorème de Rolle à la restriction de
Il suffit alors d’appliquer le théorème de Rolle à la restriction de  au segment
au segment ![Rendered by QuickLaTeX.com \left[u,v\right].](https://math-os.com/wp-content/ql-cache/quicklatex.com-28a4a4ba338ecd8d872379c44f6400e7_l3.png)
4 – Le théorème de Darboux
Etant donné un intervalle  non trivial et une application
non trivial et une application 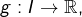 est-ce que
est-ce que 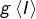 est un intervalle ?
est un intervalle ?
En général, non. Par exemple, l’application
![Rendered by QuickLaTeX.com \[g:\mathbb{R}\rightarrow\mathbb{R},\thinspace x\mapsto\left\{ \begin{array}{cc}-1 & \text{si }x\leqslant0\\1 & \text{si }x>0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9ed8342770dce141c42cba7eb255fe97_l3.png)
transforme l’intervalle

en
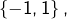
qui n’est pas un intervalle.
Pour que 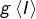 soit un intervalle, il suffit que
soit un intervalle, il suffit que 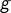 soit continue : c’est essentiellement ce que dit le théorème des valeurs intermédiaires.
soit continue : c’est essentiellement ce que dit le théorème des valeurs intermédiaires.
On doit au mathématicien français Gaston Darboux le joli résultat suivant, qui fournit une autre condition suffisante pour que 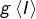 soit un intervalle : il suffit que
soit un intervalle : il suffit que 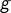 possède des primitives.
possède des primitives.
Comme on va le voir, le théorème de Darboux peut être établi grâce (notamment) au théorème CISM.
Gaston DARBOUX (1842 – 1917),
Mathématicien Français
Pour montrer que 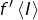 est un intervalle, on se donne
est un intervalle, on se donne 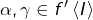 tels que
tels que 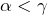 et l’on prouve que tout
et l’on prouve que tout ![Rendered by QuickLaTeX.com \beta\in\left]\alpha,\gamma\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-6e49e8075c0ee0ebf7044a20a30511c7_l3.png) est encore un élément de
est encore un élément de 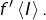
Pour cela, on introduit l’application 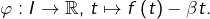
Il suffit de prouver que la dérivée de 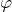 s’annule.
s’annule.
Par hypothèse, il existe 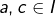 tels que
tels que 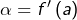 et
et 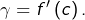
On observe que 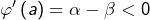 et
et 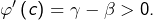 Evidemment, il n’est pas question de dire que
Evidemment, il n’est pas question de dire que 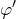 s’annule sous prétexte qu’elle change de signe : le théorème des valeurs intermédiaires ne s’applique pas à
s’annule sous prétexte qu’elle change de signe : le théorème des valeurs intermédiaires ne s’applique pas à 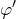 puisqu’on ne sait rien de sa continuité.
puisqu’on ne sait rien de sa continuité.
En revanche, on peut affirmer que 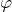 n’est pas injective, car dans le cas contraire
n’est pas injective, car dans le cas contraire 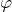 serait strictement monotone (d’après le théorème CISM) et donc sa dérivée serait de signe constant, ce qui n’est visiblement pas le cas.
serait strictement monotone (d’après le théorème CISM) et donc sa dérivée serait de signe constant, ce qui n’est visiblement pas le cas.
Ainsi, il existe 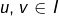 tels que
tels que 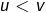 et
et 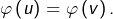 Le théorème de Rolle appliqué à la restriction de
Le théorème de Rolle appliqué à la restriction de 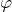 au segment
au segment ![Rendered by QuickLaTeX.com \left[u,v\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a25ea8cb3439d83d5eeadd646afbcf6d_l3.png) montre qu’il existe
montre qu’il existe ![Rendered by QuickLaTeX.com \lambda\in\left]u,v\right[](https://math-os.com/wp-content/ql-cache/quicklatex.com-d087f0048f7f79e10f6e77cb6a47538c_l3.png) tel que
tel que 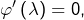 ce qui termine la preuve.
ce qui termine la preuve.
5 – Deux exercices posables à l’oral
Exercice 1
Soit 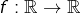 continue et telle que :
continue et telle que :
![Rendered by QuickLaTeX.com \[\forall\left(x,x'\right)\in\mathbb{R}^{2},\thinspace\left|f\left(x\right)-f\left(x'\right)\right|\geqslant\left|x-x'\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d03e6da2fb62a454b957a5f49a3c2767_l3.png)
Montrer que

est une bijection strictement monotone.
Il est clair qu’une telle application injective. En effet, si 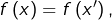 alors
alors 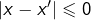 par hypothèse, c’est-à-dire
par hypothèse, c’est-à-dire 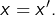 Par ailleurs,
Par ailleurs,  étant continue, le théorème CISM s’applique :
étant continue, le théorème CISM s’applique :  est strictement monotone. En outre, pour tout
est strictement monotone. En outre, pour tout 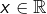 :
: 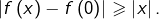 Si
Si  est croissante, il s’ensuit que :
est croissante, il s’ensuit que :
![Rendered by QuickLaTeX.com \[\left(\forall x\in\left[0,+\infty\right[,\,f\left(x\right)\geqslant x+f\left(0\right)\right)\mbox{ et }\left(\forall x\in\left]-\infty,0\right],\,f\left(x\right)\leqslant x+f\left(0\right)\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6c4b9bc8141dabed30421b3a7531ea0b_l3.png)
d’où
![Rendered by QuickLaTeX.com \[\left(\lim_{x\rightarrow-\infty}f\left(x\right)=-\infty\right)\mbox{ et }\left(\lim_{x\rightarrow+\infty}\,f\left(x\right)=+\infty\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5adecb1536fda61e53ed780ccb9ad939_l3.png)
De même, si

est décroissante,
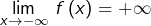
et
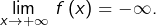
D’après le théorème des valeurs intermédiaires,

est surjective. Ainsi,

est une bijection strictement monotone.
Remarque
Une application  vérifiant l’inégalité de l’énoncé est appelée une « expansion ». Un exemple d’expansion est la fonction « sinus hyperbolique ». On peut montrer que l’ensemble des points fixes de toute expansion continue est un intervalle fermé.
vérifiant l’inégalité de l’énoncé est appelée une « expansion ». Un exemple d’expansion est la fonction « sinus hyperbolique ». On peut montrer que l’ensemble des points fixes de toute expansion continue est un intervalle fermé.
Exercice 2
Existe-t-il une injection continue de 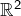 dans
dans  ?
?
Supposons l’existence d’une injection continue 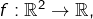 posons :
posons :
![Rendered by QuickLaTeX.com \[g:\left[0,2\pi\right]\rightarrow\mathbb{R},\thinspace t\mapsto f\left(\cos\left(t\right),\sin\left(t\right)\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4000bc83c6fc16d5e828a83d9324dc0f_l3.png)
et notons
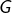
la restriction de
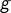
à
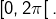
Comme
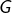
est continue, injective (car composée des injections

et
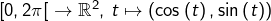
) et définie sur un intervalle, alors
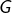
est strictement monotone d’après le théorème CISM.
Si par exemple 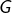 est strictement croissante, alors :
est strictement croissante, alors :
![Rendered by QuickLaTeX.com \[\forall t\in\left]\pi,2\pi\right[,\:g\left(0\right)<g\left(\pi\right)<g\left(t\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-51c7050aed7df668653752c4a3eee1e1_l3.png)
d’où, en passant à la limite lorsque
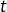
tend vers
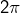
(
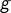
est continue en ce point) :
![Rendered by QuickLaTeX.com \[g\left(0\right)<g\left(\pi\right)\leqslant g\left(2\pi\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c808311450f719fe6d01d579ba11f4f8_l3.png)
et en particulier
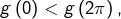
ce qui est absurde (puisque
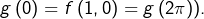
Même contradiction dans le cas où 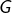 serait strictement décroissante.
serait strictement décroissante.
Finalement, il n’existe aucune injection continue de 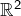 dans
dans 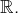
6 – Annexe : Rappels de définitions
Définition 3
Etant données deux parties 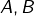 de
de 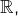 une application
une application 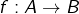 est dite continue lorsque, pour tout
est dite continue lorsque, pour tout 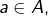 l’assertion suivante est vraie :
l’assertion suivante est vraie :
![Rendered by QuickLaTeX.com \[\forall\epsilon>0,\exists\delta>0;\forall x\in A,\thinspace\left|x-a\right|\leqslant\delta\Rightarrow\left|f\left(x\right)-f\left(a\right)\right|\leqslant\epsilon\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-01725b2fb48a4a517eef885e28baf0ae_l3.png)
Cette condition signifie qu’il est possible de rendre l’écart entre
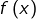
et
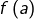
arbitrairement petit : il suffit de choisir

(dans
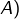
suffisamment proche de
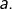
Si cet article vous a intéressé, merci de laisser un petit commentaire 🙂
![Rendered by QuickLaTeX.com \[[0,1[\rightarrow\mathbb{R},\,x\mapsto\left\{\begin{array}{cc}x+\frac12 & \text{si }0\leqslant x\leqslant\frac12\\\\x-\frac12 & \text{si }\frac12<x<1\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-412510084e2e6718cbcb7854fb2a1605_l3.png)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


