D’après l’inégalité triangulaire, il est immédiat que si  sont des nombres complexes de module 1, alors leur somme est de module inférieur ou égal à
sont des nombres complexes de module 1, alors leur somme est de module inférieur ou égal à  .
.
On se pose maintenant le problème réciproque …
Étant donnés un entier 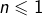 ainsi que
ainsi que 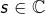 tel que
tel que 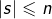 , existe-t-il
, existe-t-il  nombres complexes de module 1 et de somme
nombres complexes de module 1 et de somme  ?
?
Une solution est disponible ici
Si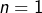 et
et  , il n'y a pas de solution.
, il n'y a pas de solution.
Autrement, la réponse est oui.
C'est évident si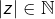 .
.
Autrement, s'il existe un entier naturel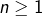 tel que
tel que 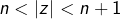 , il suffit de montrer que l'application
, il suffit de montrer que l'application 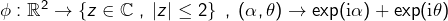 est surjective, ce qui se montre facilement en utilisant le fait que
est surjective, ce qui se montre facilement en utilisant le fait que 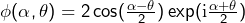 .
.
Soit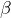 tel que
tel que 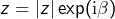 . En posant
. En posant 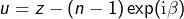 , on a
, on a 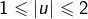 . D'après le résultat précédent, il existe deux complexes
. D'après le résultat précédent, il existe deux complexes  ,
, 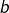 de module 1 tels que
de module 1 tels que 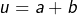 . Conclusion: si
. Conclusion: si 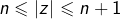 ,
, 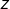 peut s'écrire comme la somme de
peut s'écrire comme la somme de  complexes de module 1.
complexes de module 1.