Soit 
décroissante, positive, deux fois dérivable et telle que 
Pour tout 
on note 
la tangente au graphe de 
au point d’abscisse 
Soit 
l’aire du triangle limité par 
et les axes de coordonnées.
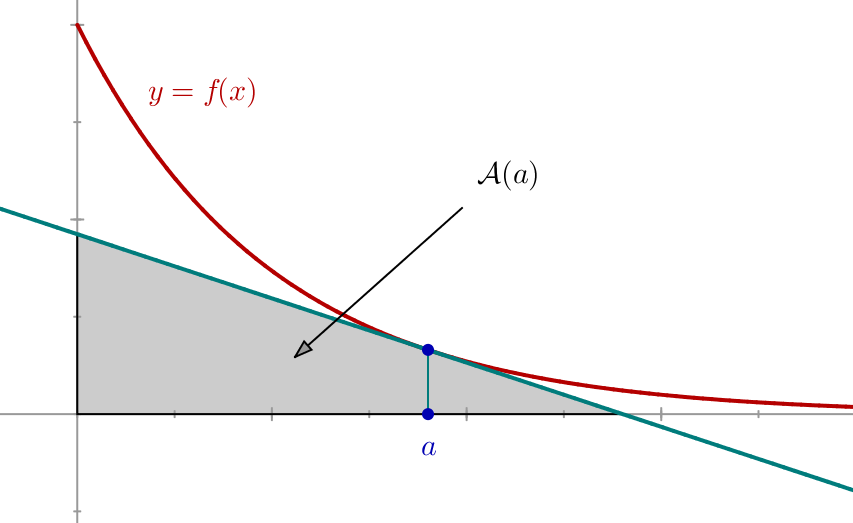
Sauriez-vous …
- calculer 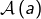explicitement ?
- étudier l’existence et (le cas échéant) la valeur de
?
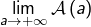Une solution est disponible ici