Un ensemble infini est qualifié de dénombrable (D, en abrégé) s’il est en bijection avec ![]() C’est le cas, entre autres, des ensembles
C’est le cas, entre autres, des ensembles ![]()
![]()
![]() et
et ![]()
Il existe des ensembles infinis non dénombrables (ND, en abrégé), comme par exemple tout intervalle de ![]() de longueur non nulle.
de longueur non nulle.
On peut assez facilement trouver des exemples de :
- familles D de parties ND de
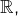 deux à deux disjointes. Exemple :
deux à deux disjointes. Exemple : 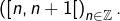
- familles ND de parties D de
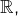 deux à deux disjointes. Exemple :
deux à deux disjointes. Exemple : 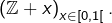
Sauriez-vous produire un exemple de famille ND de parties ND de ![]() deux à deux disjointes ?
deux à deux disjointes ?
Une solution est disponible ici


OK… J’avais un doute sur la vacuité des intersections, vous y avez répondu !
La famille des x + K où K est l’ensemble triadique de Cantor et où x décrit [0;1] – K. Je dis ça sans vérifier… Vous me direz si ça vous parait bon.
Il me semble que ces ensembles ne sont pas disjoints. Par exemple (en notation triadique) :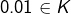 ,
, 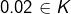 ,
, ![Rendered by QuickLaTeX.com 0.11\in[0,1]-K](https://math-os.com/wp-content/ql-cache/quicklatex.com-bdd82425c1c67b7b70c1214c396d64b0_l3.png) et
et ![Rendered by QuickLaTeX.com 0.12\in[0,1]-K](https://math-os.com/wp-content/ql-cache/quicklatex.com-9d8e6c4911221d1d06c3af6277e26e6e_l3.png) , mais
, mais 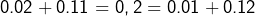 .
.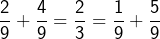 , de sorte que
, de sorte que 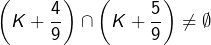 .
.
En notations fractionnaires standard :