Etant donnée une suite réelle ![]() il est connu que si
il est connu que si ![]() converge vers un réel
converge vers un réel ![]() ou bien diverge vers l’infini, alors il en va de même pour la suite de terme général :
ou bien diverge vers l’infini, alors il en va de même pour la suite de terme général :
![Rendered by QuickLaTeX.com \[X_{n}=\frac{1}{n}\sum_{k=1}^{n}u_{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6c32d461a4f8b864b68c7e7cc5328b60_l3.png)
Mais que peut-on dire dans le cas où la suite ![]() diverge, mais pas vers l’infini ? Il s’avère que la suite
diverge, mais pas vers l’infini ? Il s’avère que la suite ![]() peut alors converger ou diverger, selon le cas.
peut alors converger ou diverger, selon le cas.
Sauriez-vous trouver un exemple de chaque ? Et dans le cas de divergence, pourriez-vous faire en sorte que la suite ![]() soit bornée ?
soit bornée ?
Une solution est consultable ici


I’m amazed, I must say. Seldom do I encounter a blog
that’s both equally educative and amusing, and let me
tell you, you have hit the nail on the head. The problem
is something that not enough people are speaking intelligently about.
I am very happy that I came across this in my hunt for something concerning this.
Ben alors là, je pense que j’ai bien fait de ne pas trop me creuser la tête, parmi les idées que j’ai eues, aucune n’allait dans cette direction. Je lirai ça attentivement plus tard pour me convaincre (là, c’est l’heure du derby entre le Réal et l’Atlético !). Je vous signale juste un petit problème de typographie : la ligne avant « et donc, si n est impair alors « … Le rang du terme de la suite X n’est pas écrit en indice.
Dans ce cas, ça me semble impossible, mais je vais attendre votre solution pour comprendre quelle possibilité je n’ai pas envisagée !
Une solution est en ligne ! Bonne lecture.
OK, il me semblait bien que dans cette acception c’était un peu trop simple pour constituer un challenge. Du coup, que faut-il s’interdire ? Que |u| tende vers +\infty ? Ou bien qu’une suite extraite de u ne le fasse ?
Merci pour la mise en forme de ma réponse initiale. Je ne sais pas si ça marche si on tape directement du code LaTeX, Là je viens d’essayer, je vais bien voir… Mais il y a peut-être des balises à mettre.
PS : Pendant que vous y étiez, vous auriez pu corriger ma phrase tapée trop vite : un mot qui manque et un autre en trop !
Pour , il vous suffit d’encadrer les formules par une paire de $.
, il vous suffit d’encadrer les formules par une paire de $.
Pour le contre-exemple demandé, je propose de chercher une suite réelle bornée u, pour laquelle la suite X diverge.
Et j’ai rectifié les deux typos dans votre précédent message : c’est le genre de truc qui échappe à la lecture … comme si notre cerveau corrigeait tout seul.
Bonjour, diverge vers
diverge vers 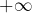 lorsque
lorsque 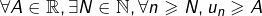 . Toujours par définition, on dit que la suite
. Toujours par définition, on dit que la suite  diverge vers
diverge vers 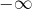 lorsque la suite opposée diverge vers
lorsque la suite opposée diverge vers 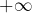 .
.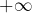 ni vers
ni vers 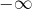 . La suite de terme général
. La suite de terme général 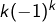 , que vous avez proposée, entre donc bien dans ce cadre.
, que vous avez proposée, entre donc bien dans ce cadre.
Vous avez raison, dire d’une suite réelle « qu’elle diverge, mais pas vers l’infini » peut effectivement soulever une ambigüité. Alors je m’explique (pas pour vous, qui avez décelé l’ambigüité, mais pour d’autres qui nous liront).
Par définition, on dit que la suite
Une suite réelle qui diverge, mais pas vers l’infini serait donc une suite non convergente et ne divergeant ni vers
Cela dit, votre commentaire m’a fait réaliser que je n’avais pas posé exactement la bonne question. Je vais donc étoffer un peu l’énoncé !