Soient et deux entiers impairs strictement supérieurs à 1.

Leur produit peut s’écrire comme une somme d’entiers naturels impairs et consécutifs (cette somme comportant au moins deux termes… et même trois, pour des raisons évidentes de parité).

Par exemple :

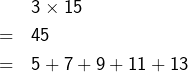
Sauriez-vous prouver cela en toute généralité ?

A quelle condition sur les entiers et une telle écriture est-elle unique ?

Une solution est disponible ici