Deux ensembles de Julia très simples

Etant donné $c\in\mathbb{C},$ on considère pour tout $s\in\mathbb{C}$ la suite $\left(z_{n}\right)_{n\geqslant0}$ définie par :

$\fcolorbox{black}{myBlue}{$\displaystyle{z_{0}=s\qquad\text{et}\qquad\forall n\in\mathbb{N},\thinspace z_{n+1}=z_{n}^{2}+c}$}$

L’ensemble de Julia rempli est, par définition:

$\fcolorbox{black}{myBlue}{$\displaystyle{K_{c}=\left\{ s\in\mathbb{C};\thinspace z_{n}\not\longrightarrow\infty\right\}}$}$

qui est une partie compacte et non vide de $\mathbb{C}$ .

Un théorème de Fatou et Julia (1919) indique que $K_{c}$ est connexe ou totalement discontinu, selon la valeur de $c$ (voir illustrations en fin d’article).

L’ensemble des $c\in\mathbb{C}$ pour lesquels $K_{c}$ est connexe est l’ensemble de Mandelbrot, noté $M$ :

L’objet de cette note est de décrire $K_{c}$ dans deux cas particuliers très simples (les seuls) :

pour $c=0$
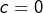
pour $c=-2.$

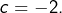
Le cas c = 0

Proposition

$K_{0}$ est le disque unité fermé.

Lorsque $c=0,$ la suite $\left(z_{n}\right)$ est définie par :

$\forall n\in\mathbb{N},\thinspace z_{n}=s^{2^{n}}$

Attention : il s’agit de $s^{\left(2^{n}\right)}$ et pas de $\left(s^{2}\right)^{n}$ …

A chaque étape de l’itération, le module est élevé au carré et l’argument est doublé.

➡ Si $\left|s\right|\leqslant1,$ alors $\forall n\in\mathbb{N},\thinspace\left|z_{n}\right|\leqslant1,$ ce qui prouve que $s\in K_{0}.$ Donc : $\overline{D\left(0,1\right)}\subset K_{0}.$

➡ Si $\left|s\right|>1,$ alors la suite $\left(z_{n}\right)$ diverge en module vers $+\infty,$ puisqu’elle est extraite de la suite géométrique $\left(s^{n}\right)$ (qui possède ce comportement). Donc : $K_{0}\subset\overline{D\left(0,1\right)}.$

On peut visualiser ces comportements …

Pour $\left|s\right|<1,$ on voit les premiers termes de la suite $\left(z_{n}\right)$ spiraler vers l’origine :

Pour $\left|z\right|>1,$ la spirale se déroule à l’extérieur du disque unité :

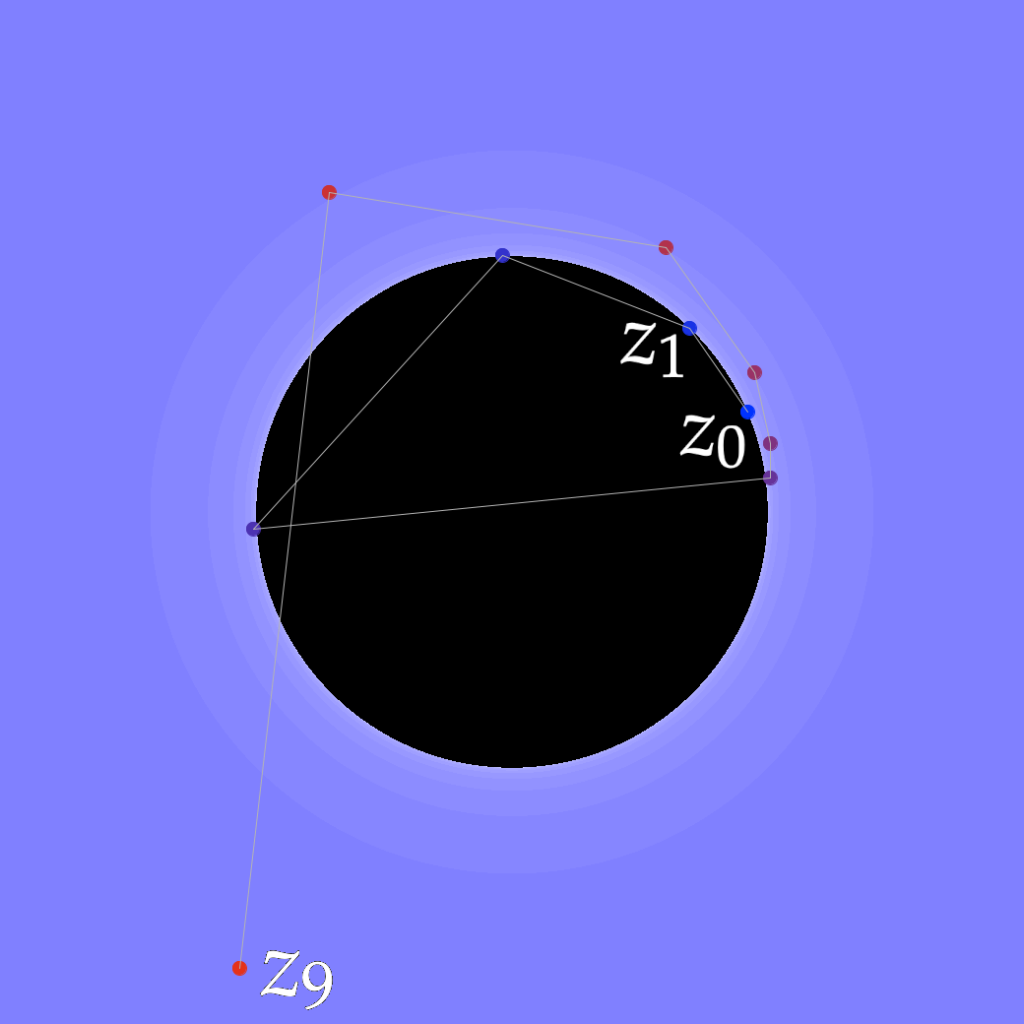
Bref :

$\fcolorbox{black}{myBlue}{$\displaystyle{K_{0}=\overline{D}\left(0,1\right)}$}$

Remarque

Il est frappant de constater que lorsque la suite $\left(z_{n}\right)$ diverge, elle diverge pour de bon ! Supposons par exemple que $\left|s\right|=1.1$ et calculons les modules des premiers termes :

$\left|z_{1}\right|=1.21$

$\left|z_{2}\right|\simeq1.46$

$\left|z_{3}\right|\simeq2.14$

$\left|z_{4}\right|\simeq4.59$

$\left|z_{5}\right|\simeq21.11$

Un peu plus loin :

$\boxed{\left|z_{10}\right|=2.4\times10^{42}}$

Si l’unité de longueur est le centimètre, alors le cinquième terme se trouve à une bonne vingtaine de centimètres de l’origine … et le dixième est situé à plus de vingt milliards de milliards de milliards de milliards de kilomètres … Une distance très supérieure au diamètre de l’univers connu !!

Par Fernando Pena — https://www.flickr.com/photos/drcaosastrophoto/49804340298/, CC BY 2.0, https://commons.wikimedia.org/w/index.php?curid=129107601

Le cas c = -2

Lemme (Transformée de Joukowski)

Notons $\Delta=\left\{ z\in\mathbb{C};\thinspace0<\left|z\right|<1\right\} .$

Alors l’application $J:\Delta\rightarrow\mathbb{C}-\left[-2,2\right],\thinspace z\mapsto z+\dfrac{1}{z}$ est une bijection, qui « conjugue » les applications $\Delta\rightarrow\Delta,\thinspace z\mapsto z^{2}$ et $\mathbb{C}-\left[-2,2\right]\rightarrow\mathbb{C}-\left[-2,2\right],\thinspace z\mapsto z^{2}-2.$

Notons $\varphi:\mathbb{C}-\left\{ 0\right\} \rightarrow\mathbb{C},\thinspace z\mapsto z+\dfrac{1}{z}.$

Pour tout $z\in\mathbb{C}-\left\{ 0\right\} ,$ si $\varphi\left(z\right)\in\left[-2,2\right],$ alors il existe $\theta\in\mathbb{R}$ tel que :

$z+\dfrac{1}{z}=2\cos\left(\theta\right)$

c’est-à-dire $z^{2}-2z\cos\left(\theta\right)+1=0,$ ou encore $\left(z-e^{i\theta}\right)\left(z-e^{-i\theta}\right)=0$ et donc $z\in\mathbb{U}.$ En particulier $z\notin\Delta.$ Par contraposée, si $z\in\Delta$ alors $\varphi\left(z\right)\in\mathbb{C}-\left[-2,2\right].$

On peut donc bien définir une application

$\boxed{J:\Delta\rightarrow\mathbb{C}-\left[-2,2\right],\thinspace z\mapsto z+\dfrac{1}{z}}$

Soient $z,w\in\Delta$ tels que $J\left(z\right)=J\left(w\right).$ Alors, après multiplication par $zw$ et mise en facteur, il vient :

$\left(zw-1\right)\left(z-w\right)=0$

Mais $\left|zw\right|=\left|z\right|\thinspace\left|w\right|<1,$ donc $zw\neq1$ et donc $z=w.$ Ceci prouve l’injectivité de $J.$ Par ailleurs, étant donné $w\in\mathbb{C}-\left[-2,2\right],$ on sait que $w$ possède deux antécédents par $\varphi$ : ce sont les solutions $z_{1}$ et $z_{2}$ de l’équation $z^{2}-wz+1=0.$ On a donc $z_{1}z_{2}=1$ (produit des racines d’un trinôme) et, de plus $\left|z_{1}\right|\neq1$ et $\left|z_{2}\right|\neq1$ (car l’image par $\varphi$ d’un élément de $\mathbb{U}$ appartient à $\left[-2,2\right]).$ Ainsi $\left|z_{1}\right|<1$ ou $\left|z_{2}\right|<1$ : l’un des antécédents de $w$ par $\varphi$ appartient à $\Delta,$ ce qui prouve la surjectivité de $J.$

Ainsi :

$\fcolorbox{black}{myBlue}{$\displaystyle{J\text{ est une bijection}}$}$

Enfin, pour tout $z\in\Delta$ :

$J\left(z\right)^{2}-2=\left(z+\dfrac{1}{z}\right)^{2}-2=z^{2}+\dfrac{1}{z^{2}}=J\left(z^{2}\right)$

Donc, en notant

$F:\Delta\rightarrow\Delta,\thinspace z\mapsto z^{2}$

$G:\mathbb{C}-\left[-2,2\right]\rightarrow\mathbb{C}-\left[-2,2\right],\thinspace z\mapsto z^{2}-2$

il vient :

$\fcolorbox{black}{myBlue}{$\displaystyle{F=J^{-1}\circ G\circ J}$}$

Proposition

$K_{-2}$ est le segment réel $\left[-2,2\right].$

Si $s\in\left[-2,2\right],$ alors il existe $\theta\in\left[0,\pi\right]$ tel que $s=2\cos\left(\theta\right),$ d’où :

$z_{1}=s^{2}-2=4\cos^{2}\left(\theta\right)-2=2\left(2\cos^{2}\left(\theta\right)-1\right)=2\cos\left(2\theta\right)$

puis, par récurrence :

$\forall n\in\mathbb{N},\thinspace z_{n}=2\cos\left(2^{n}\theta\right)\in\left[-2,2\right]$

Ceci montre en particulier que la suite $\left(z_{n}\right)_{n\geqslant0}$ est bornée et donc que $\boxed{\left[-2,2\right]\subset K_{-2}}$

Par ailleurs, si $s\in\mathbb{C}-\left[-2,2\right],$ le lemme montre qu’il existe (un unique) $u\in\Delta$ tel que $s=u+\dfrac{1}{u}.$ Alors :

$z_{1}=s^{2}-2=\left(u+\dfrac{1}{u}\right)^{2}-2=u^{2}+\dfrac{1}{u^{2}}$

et par récurrence :

$\forall n\in\mathbb{N},\thinspace z_{n}=u^{2^{n}}+\dfrac{1}{u^{2^{n}}}$

Ainsi ${\displaystyle \lim_{n\rightarrow+\infty}\left|z_{n}\right|=+\infty},$ donc $s\notin K_{-2}.$ Ceci montre que $\boxed{K_{-2}\subset\left[-2,2\right]}$

Finalement :

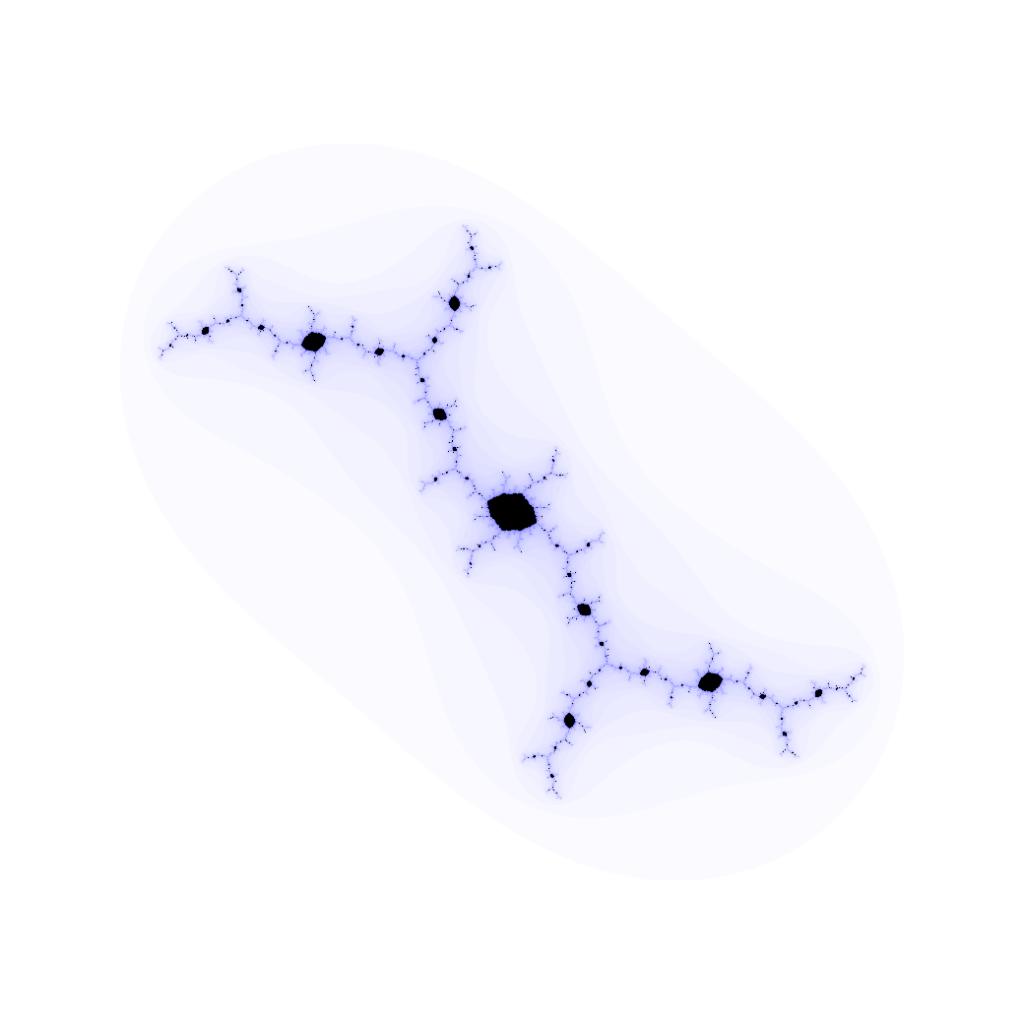
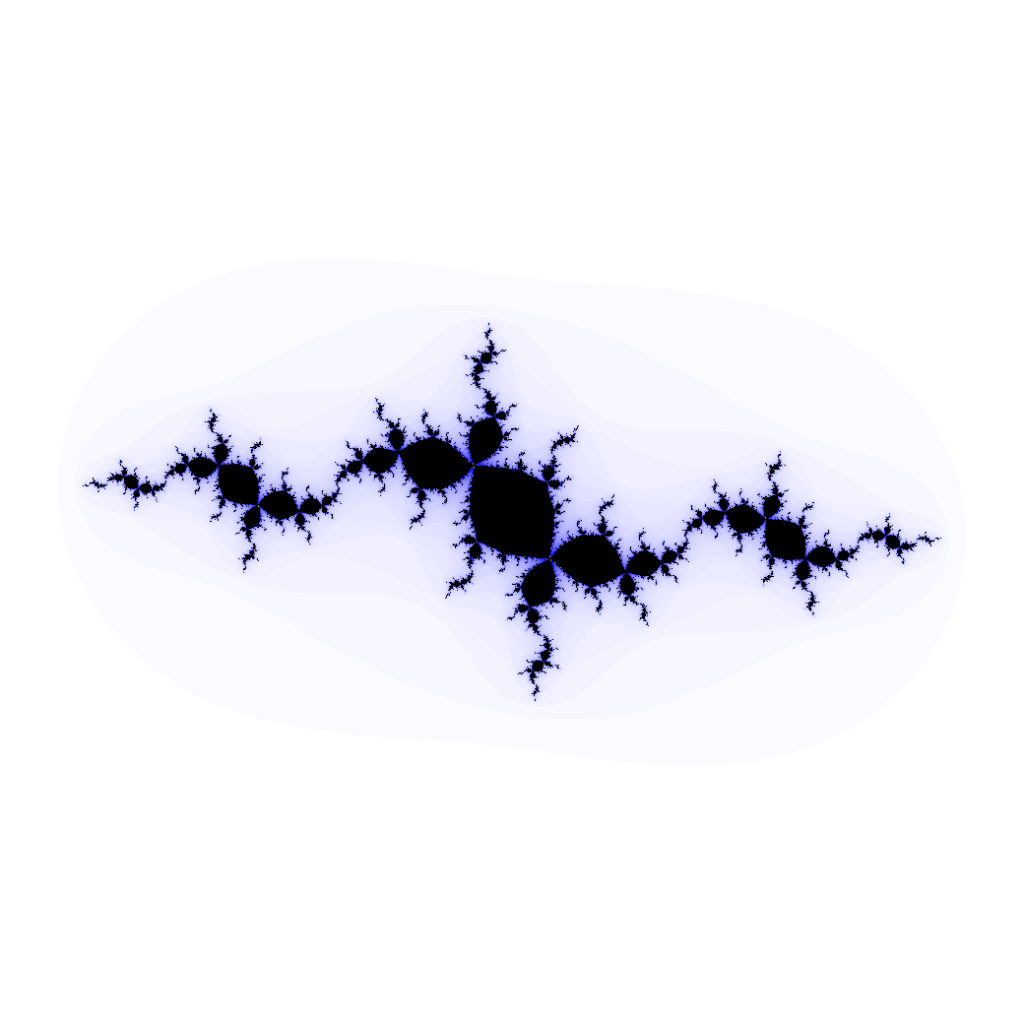
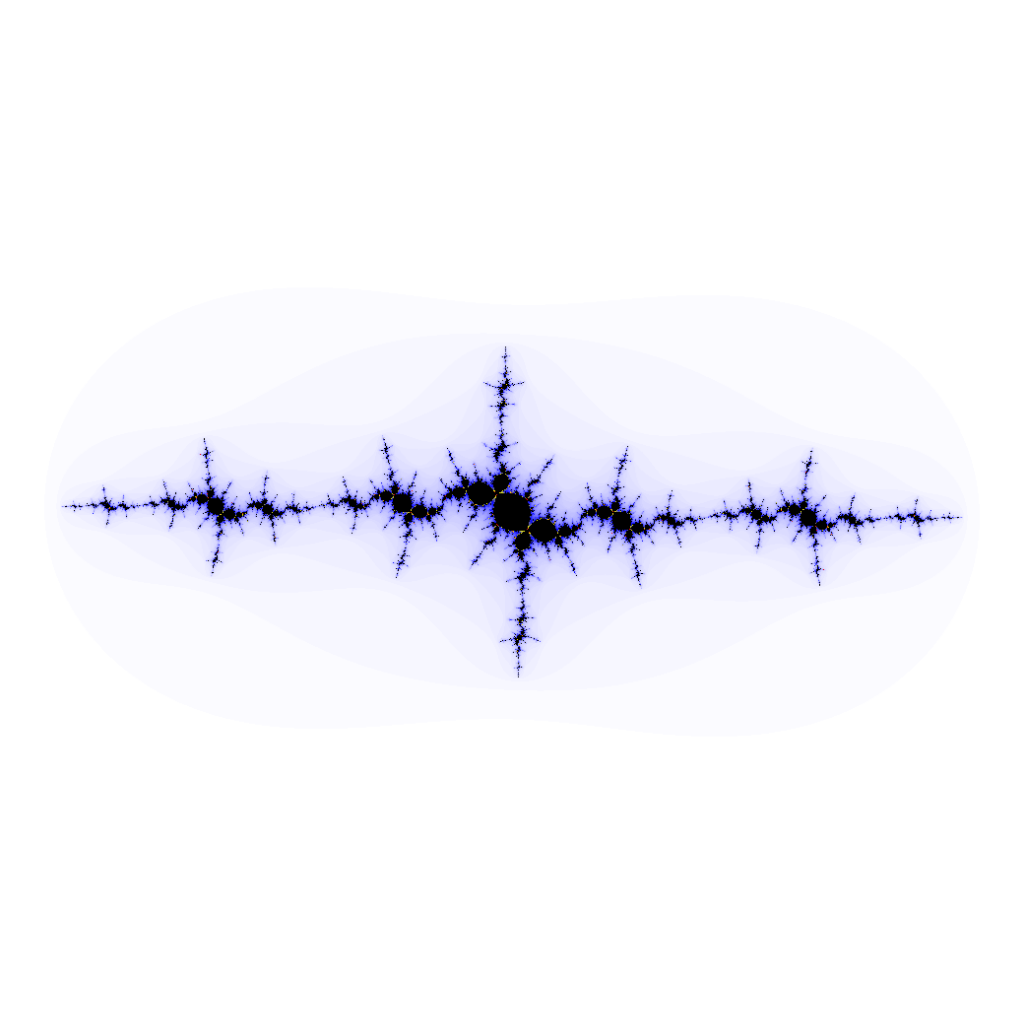
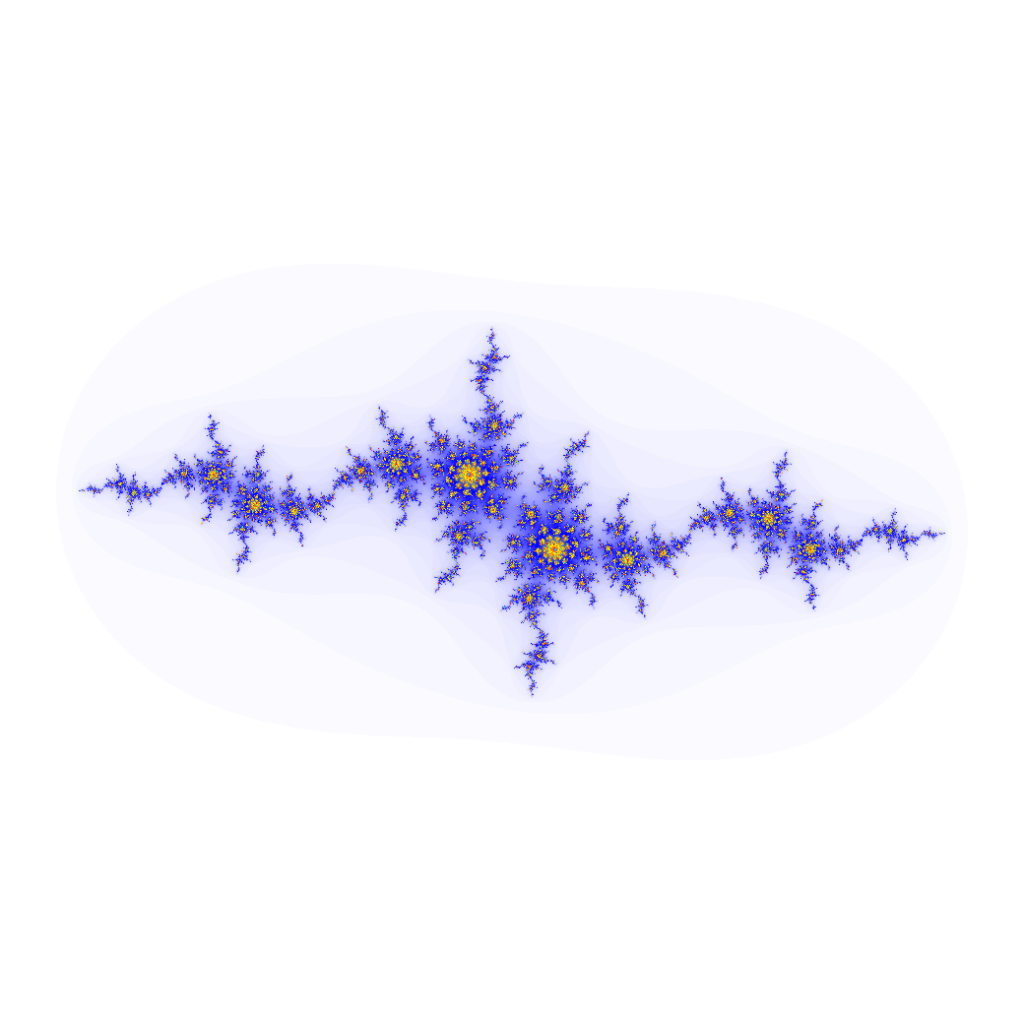
$\fcolorbox{black}{myBlue}{$\displaystyle{K_{-2}=\left[-2,2\right]}$}$

A quoi ressemblent les autres ensembles de Julia ?

Lorsque $c$ prend d’autres valeurs, l’ensemble $K_{c}$ possède une structure infiniment plus riche et plus difficile à décrire … Lorsqu’on zoome sur sa frontière, on voit essentiellement le même paysage, peu importe l’échelle. Pour cette raison, on parle d’ensemble « fractal » :

Ci-dessous, sont représentés quelques ensembles de Julia remplis, pour diverses valeurs du paramètre $c.$ Les 7 premiers sont connexes. Les 2 suivants aussi, mais de mesure nulle. Les 3 derniers sont totalement discontinus. Pour ces 5 dernières illustrations, on ne « voit » pas véritablement $K_{c}$ (aucun pixel noir sur l’image), mais on devine sa présence au fond d’une vallée …