A propos des sommes géométriques

Une fois n’est pas coutume, cet article est considéré comme étant à la fois de niveau lycée et de niveau supérieur. Il comporte en effet des aspects élémentaires (sections 1 à 5) mais aussi un peu de matériel plus avancé (sections 6, 7 et 8).

Après s’être donné deux nombres réels $s\text{ et }q,$ posons pour tout $n\in\mathbb{N}$ :

$\boxed{u_{n}=s\:q^{n}}\qquad\text{formule explicite}$

Une telle suite $\left(u_{n}\right)_{n\geqslant0}$ est dite géométrique de raison $q,$ ce qui signifie qu’on passe d’un terme au suivant en multipliant par $q.$

On peut définir la même suite par les relations :

$\boxed{\left.\begin{matrix}u_{0} = s\\ \forall n\in\mathbb{N}, u_{n+1}=q\thinspace u_{n}\end{matrix}\right\}}\qquad\text{formule de récurrence}$

Par exemple, si $s=3$ et $q=2,$ alors les premiers termes de la suite sont :

$u_{0}=3,\quad u_{1}=6,\quad u_{2}=12,\quad u_{3}=24,\quad u_{4}=48,\quad\text{etc …}$

Le but de cet article est de rassembler diverses remarques au sujet des sommes de la forme :

$\boxed{S_{p,n}=\sum_{k=p}^n u_k}\qquad\text{avec }0\leqslant p\leqslant n$

Ces sommes sont appelées : sommes géométriques de raison $q.$

Si vous n’êtes pas tout à fait à l’aise avec l’utilisation du symbole $\Sigma,$ je vous invite à parcourir au préalable le début de cet article.

1 – Une formule archi-classique

Pour des raisons assez évidentes, il n’est pas restrictif de supposer $s=1,$ ce qu’on fera désormais.

Le résultat suivant est fondamental. Il est recommandé de le connaître par cœur :

Proposition

Pour tout nombre réel $q\neq1$ et pour tout $n\in\mathbb{N}$ :

( $\heartsuit$ ) $\boxed{\sum_{k=0}^{n}q^{k}=\frac{1-q^{n+1}}{1-q}}$

Bien sûr, si $q=1,$ cette somme vaut $n+1$ (elle comporte $n+1$ termes, tous égaux à 1).

Preuve (cliquer pour déplier / replier)

Par récurrence. La formule annoncée est vraie pour n = 0.

En la supposant vraie pour un certain $n\in\mathbb{N},$ on constate que :

$\sum_{k=0}^{n+1}q^{k}=\frac{1-q^{n+1}}{1-q}+q^{n+1}=\frac{1-q^{n+1}+q^{n+1}\left(1-q\right)}{1-q}$

soit finalement :

$\sum_{k=0}^{n+1}q^{k}=\frac{1-q^{n+2}}{1-q}$

comme souhaité.

Précisons que cette formule reste plus généralement valable en choisissant pour $q$ un nombre complexe distinct de 1. Cette remarque sera utile pour les calculs menés à la section 7.

Ajoutons encore que si $\left|q\right|<1,$ alors un simple passage à la limite nous donne la somme d’une série géométrique convergente :

$\sum_{k=0}^{\infty}q^{k}=\frac{1}{1-q}$

2 – Petite fable géométrique

On raconte qu’il y a très longtemps, dans un lointain royaume, un roi voulut récompenser l’un de ses sujets, qui s’était vaillamment illustré au champ de bataille. Il le convoqua à la cour et s’adressa à lui en ces termes :

— Fidèle soldat, je suis prêt à te couvrir de richesses, car tu t’es battu avec bravoure. Demande-moi ce que tu voudras et, dans ma toute-puissance, je t’exaucerai.

— Ben euh … majesté … merci. Mais je ne sais pas trop …

— Allons allons ! je suis ton Roi … et tu peux me demander n’importe-quoi.

— Eh bien alors, majesté, si vous insistez …

— Oui ?

— La guerre a rendu ces dernières années bien difficiles et j’aimerais que vous m’aidiez à mettre les miens à l’abri de la famine. Nos réserves de sucre sont épuisées et vous pourriez m’aider à les reconstituer …

— Noble demande que la tienne ! De combien de sucre penses-tu avoir besoin ?
Tu peux demander ce que tu veux à ton Roi.

— Votre altesse est trop bonne. Eh bien, disons que sur un échiquier de 64 cases, vous pourriez dire à vos gens qu’ils déposent un morceau de sucre sur la première case, trois sur la seconde, neuf sur la troisième, vingt-sept sur la suivante, puis quatre-vingt un … et ainsi de suite jusqu’à la dernière case.

— Voilà une requête bien modeste. Rentre chez toi, à présent. Je ferai en sorte que, dès demain matin, mes gardes t’apportent la quantité de sucre que tu réclames.

Evidemment, le roi n’a jamais pu satisfaire cette demande exorbitante.

Il aurait en effet fallu qu’il rassemble $N$ morceaux de sucre, avec :

$N=1+3+3^2+3^3+3^4+\cdots+3^{63}$

c’est-à-dire, selon la formule $\left(\heartsuit\right)$ :

$N=\frac{3^{64}-1}{2}$

Sous cette forme, ça n’a peut-être l’air de rien. Mais le calcul donne :

$\boxed{N=1\thinspace716\thinspace841\thinspace910\thinspace146\thinspace256\thinspace242\thinspace328\thinspace924\thinspace544\thinspace640}$

soit plus de 1700 milliards de milliards de milliards de morceaux de sucre …

Tous les champs de canne à sucre de la planète n’y suffiraient pas.

Afin de mieux se représenter la chose, imaginons que la surface du globe terrestre soit une sphère bien lisse et qu’on y répartisse uniformément tous ces morceaux de sucre.

🤔 Quelle serait alors l’épaisseur de la couche de sucre recouvrant la terre ?

Allez, faites votre calcul (en considérant qu’un morceau de sucre occupe un volume de 1 $cm^{3})$ et rendez-vous en annexe pour voir si on est d’accord …

3 – Retour sur la formule $\left(\heartsuit\right)$

On est parfois conduit, au cours d’un calcul, à simplifier une expression du type :

$G_{p,n}=\sum_{k=p}^{n}q^{k}\qquad\text{pour }q\in\mathbb{C}-\left\{ 1\right\}\text{ et }0\leqslant p\leqslant n$

Il est facile, en mettant $q^{p}$ en facteur, de se ramener à la formule $\left(\heartsuit\right).$ En effet :

$G_{p,n}=q^{p}\sum_{k=p}^{n}q^{k-p}$

d’où, après le changement d’indice $j=k-p$ :

$G_{p,n}=q^{p}\sum_{j=0}^{n-p}q^{j}=\frac{q^{p}\left(1-q^{n-p+1}\right)}{1-q}$

soit finalement :

$\boxed{G_{p,n}=\frac{q^{p}-q^{n+1}}{1-q}}\qquad\left(\star\star\right)$

Certains ont l’habitude de mémoriser cette formule ainsi :

$\boxed{\frac{\left(\text{premier terme}\right)-\left(\text{dernier terme}\right)\times\left(\text{raison}\right)}{1-\text{raison}}}$

Evidemment, on parvient au même résultat en considérant que :

$G_{p,n}=\sum_{k=0}^{n}q^{k}-\sum_{k=0}^{p-1}q^{k}=\frac{1-q^{n+1}}{1-q}-\frac{1-q^{p}}{1-q}$

puis en simplifiant cette dernière expression.

4 – Lien avec une célèbre identité remarquable

La formule suivante est classique :

Factorisation d’une différence de puissances n-èmes

Etant donnés un entier $n\geqslant2$ et un couple $\left(a,b\right)$ de nombres complexes :

( $\blacklozenge$ ) $\boxed{a^{n}-b^{n}=\left(a-b\right)\sum_{k=1}^{n}a^{k-1}b^{n-k}}$

Ceci se prouve aisément par récurrence.

Preuve (cliquer pour déplier / replier)

Fixons $\left(a,b\right)\in\mathbb{C}^{2}$ et montrons que l’assertion :

$\left(\mathcal{A}_{n}\right):\qquad a^{n}-b^{n}=\left(a-b\right)\sum_{k=1}^{n}a^{k-1}b^{n-k}$

est vraie pour tout entier $n\geqslant2$ .

➡ D’évidence, $\left(\mathcal{A}_{2}\right)$ est vraie. Il s’agit de l’égalité

$a^2-b^2=(a-b)(a+b)$

bien connue dès la fin du collège (normalement).

➡ En supposant $\left(\mathcal{A}_{n}\right)$ vraie pour un certain $n\geqslant2,$ on observe que :

$\begin{equation*}\begin{split}a^{n+1}-b^{n+1} & = a\left(a^{n}-b^{n}\right)+ab^{n}-b^{n+1}\\& = a\left(a-b\right)\left(\sum_{k=1}^{n}a^{k-1}b^{n-k}\right)+\left(a-b\right)b^{n}\\& = \left(a-b\right)\left[\left(\sum_{k=1}^{n}a^{k}b^{n-k}\right)+b^{n}\right]\end{split}\end{equation*}$

En effectuant le changement d’indice $j=k+1,$ il vient :

$\begin{equation*}\begin{split}a^{n+1}-b^{n+1} & = \left(a-b\right)\left[\left(\sum_{j=2}^{n+1}a^{j-1}b^{n+1-j}\right)+b^{n}\right]\end{split}\end{equation*}$

soit finalement :

$a^{n+1}-b^{n+1}=\left(a-b\right)\sum_{j=1}^{n+1}a^{j-1}b^{n+1-j}$

comme souhaité.

Il est facile de constater que les formules $\left(\blacklozenge\right)$ et $\left(\heartsuit\right)$ se déduisent l’une de l’autre. En effet :

➡ Si l’on dispose de $\left(\blacklozenge\right)$ et si $q\in\mathbb{C}-\left\{ 1\right\} ,$ il suffit de choisir $a=q$ et $b=1$ pour obtenir $\left(\heartsuit\right).$

⬅ Réciproquement, si l’on connaît $\left(\heartsuit\right)$ alors étant donnés $a,b\in\mathbb{C}$ tels que $a\neq0$ et $b\neq a,$
on voit que :

$\begin{equation*}\begin{split}\sum_{k=0}^{n-1}\left(\frac{b}{a}\right)^{k} & = \frac{1-\left(\frac{b}{a}\right)^{n}}{1-\frac{b}{a}}\\& = \frac{1}{a^{n-1}}\:\frac{a^{n}-b^{n}}{a-b}\end{split}\end{equation*}$

d’où $\left(\blacklozenge\right)$ en multipliant chaque membre par $a^{n -1}\left(a-b\right).$
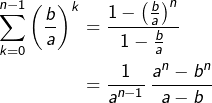
Et bien sûr la formule $\left\blacklozenge\right)$ est vraie si $a=0$ ou $a=b$ .

5 – Aire d’un domaine fractal

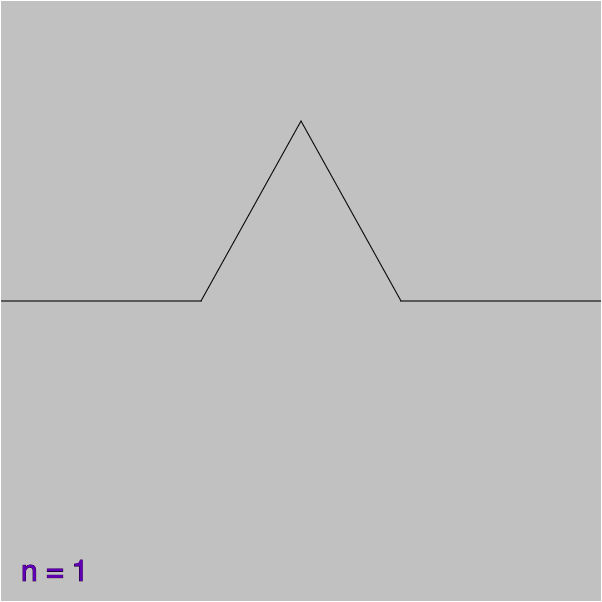
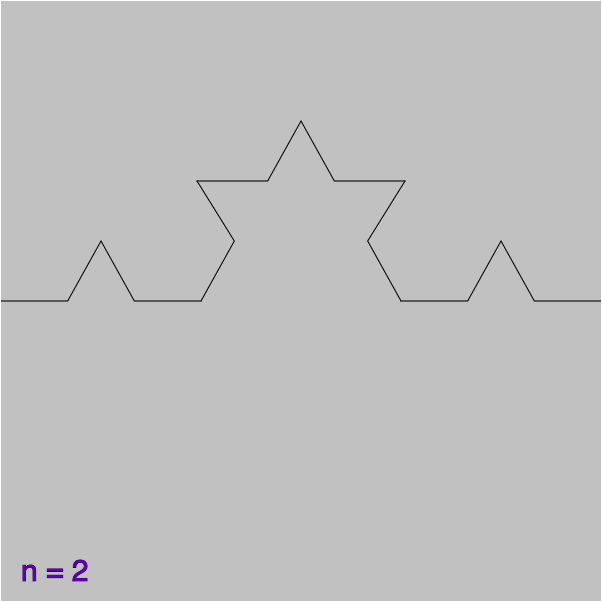
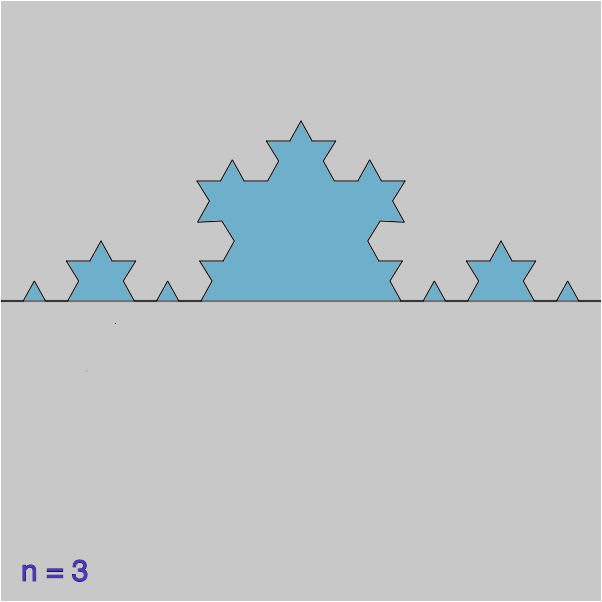
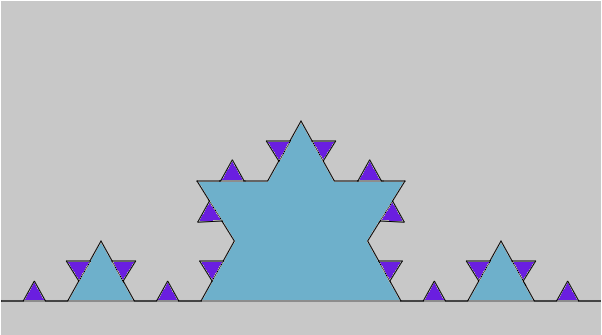
Une ligne polygonale est une succession de segments de droites, chaque segment (du premier à l’avant-dernier) ayant pour extrémité l’origine du segment suivant. Les dessins ci-dessous montrent des lignes polygonales notées $L_{0},$ $L_{1},$ $L_{2},$ etc …

On suppose que $L_{0}$ est de longueur 1 et l’on se propose de calculer l’aire du domaine $D_{n}$ « compris entre $L_{n}$ et $L_{0}$ » (ci-dessous, $D_{3}$ est colorié en bleu).

On devine que la suite $(L_n)_{n\geqslant0}$ converge (encore faudrait-il préciser en quel sens … car il ne s’agit pas d’une suite de nombres réels, mais bien d’une suite de parties de $\mathbb{R}^2$ ). L’objet limite est la fractale de Von Koch, ainsi nommée en hommage au célèbre mathématicien suédois.

Notons $\ell_{n}$ la longueur de $L_{n}$ et $d_{n}$ l’aire du domaine $D_{n}.$

On observe que la ligne polygonale $L_{n+1}$ est constituée de quatre copies de $L_{n},$ ayant subi chacune une similitude (directe) de rapport $\frac{1}{3}$ (pour le dire simplement : une réduction au tiers de la taille). Ainsi :

$\begin{equation*}\begin{split}\ell_{n+1} & = \frac{4}{3}\ell_{n}\end{split}\end{equation*}$

La suite $\left(\ell_{n}\right)_{n\geqslant0}$ est donc géométrique de raison $\frac{4}{3}.$ Comme $\ell_{0}=1,$ on en déduit que :

$\boxed{\forall n\in\mathbb{N},\:\ell_{n}=\left(\frac{4}{3}\right)^{n}}$

Quant au domaine $D_{n+1},$ il est l’union de $D_{n}$ et de $4^{n}$ triangles équilatéraux, chacun étant l’image d’un triangle équilatéral de côté 1 par une similitude de rapport $\frac{1}{3^{n+1}}.$

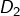Le domaine $D_2$ en bleu, complété par l’union de 16 triangles pour former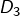 $D_3$

Attention :

Par une similitude de rapport $k>0,$
les longueurs sont multipliées par $k$
mais les aires sont multipliées par $k^{2}.$

On a donc, pour tout $n\in\mathbb{N}$ :

$d_{n+1}=d_{n}+4^{n}\frac{\sqrt{3}}{4}\left(\frac{1}{3^{n+1}}\right)^{2}$

c’est-à-dire :

$d_{n+1}=d_{n}+\frac{\sqrt{3}}{36}\left(\frac{4}{9}\right)^{n}$

Après sommation télescopique (et vu que $d_{0}=0)$ :

$d_{n}=\sum_{k=0}^{n-1}\left(d_{k+1}-d_{k}\right)=\frac{\sqrt{3}}{36}\sum_{k=0}^{n-1}\left(\frac{4}{9}\right)^{k}$

c’est-à-dire, selon la formule $\left(\heartsuit\right)$ :

$d_{n}=\frac{\sqrt{3}}{36}\frac{1-\left(\frac{4}{9}\right)^{n}}{1-\frac{4}{9}}$

soit finalement :

$\boxed{\forall n\in\mathbb{N},\thinspace d_{n}=\frac{\sqrt{3}}{20}\left(1-\left(\frac{4}{9}\right)^{n}\right)}$

La suite $\left(\ell_{n}\right)_{n\in\mathbb{N}}$ diverge donc vers l’infini tandis que la suite $\left(d_{n}\right)_{n\in\mathbb{N}}$ converge !

La limite de la suite des aires est donnée par :

$\lim_{n\to\infty}d_n=\frac{\sqrt{3}}{20}\simeq0,0866$

Cette valeur est un peu inférieure au tiers de l’aire du triangle rectangle isocèle englobant (c’est-à-dire : $\frac{1}{3}\times\frac{1}{4}\simeq0,0833)$ , ce qui paraît en accord avec la figure ci-dessous :

Noter que l’on pouvait obtenir beaucoup plus vite l’aire du domaine limite, en considérant (cf. figure ci-dessous) qu’il est l’union de $D_1$ (dont l’aire est celle du triangle équilatéral de côté $\frac13$ , représenté en bleu) et de 4 copies en réduction du même domaine limite (représentées en vert) :

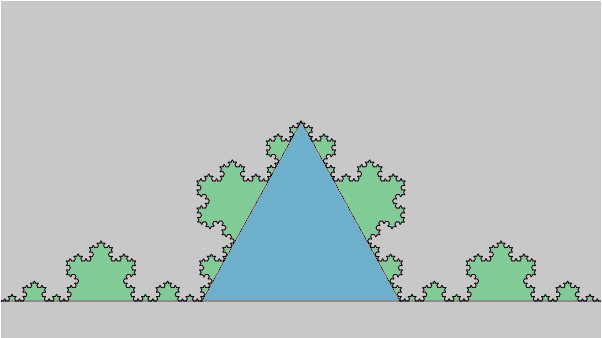
Ainsi :

$d=\frac{\sqrt3}{36}+4\frac{d}{9}$

ce qui redonne bien :

$d=\frac{\sqrt3}{20}$

6 – Dérivation d’une somme géométrique

On souhaite trouver une formule explicite pour :

$P_{n}\left(x\right)=\sum_{k=1}^{n}k\thinspace x^{k}\qquad\text{avec }n\in\mathbb{N}^{\star}\text{ et }x\in\mathbb{R}-\left\{ 1\right\}$

Pour cela, on dispose d’au moins quatre stratégies différentes …

➡ Stratégie 1 : par télescopie

On observe que :

$\begin{equation*}\begin{split}\left(1-x\right)P_{n}\left(x\right) & = \sum_{k=1}^{n}\left(kx^{k}-kx^{k+1}\right)\\& = \sum_{k=1}^{n}\left(kx^{k}-\left(k+1\right)x^{k+1}\right)+\sum_{k=1}^{n}x^{k+1}\end{split}\end{equation*}$

donc, d’après $\left(\star\star\right)$ :

$\left(1-x\right)P_{n}\left(x\right)=x-\left(n+1\right)x^{n+1}+\frac{x^{2}\left(1-x^{n}\right)}{1-x}$

soit, après simplification :

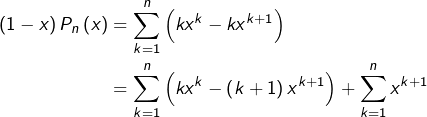
$\fcolorbox{black}{myBlue}{$\displaystyle{P_{n}\left(x\right)=\frac{nx^{n+2}-\left(n+1\right)x^{n+1}+x}{\left(1-x\right)^{2}}}$}$

Il est intéressant de noter que pour $\left|x\right|<1,$ on obtient après passage à la limite :

$\sum_{k=1}^{\infty}k\thinspace x^{k}=\frac{x}{\left(1-x\right)^{2}}$

Remarque

Cette formule intervient en probabilités, lorsqu’on calcule l’espérance d’une loi géométrique.

En effet, étant donné $p\in\left]0,1\right[$ et une variable aléatoire dont la loi est donnée par :

$\forall k\in\mathbb{N}^{\star},\thinspace\mathbb{P}\left(X=k\right)=\left(1-p\right)^{k-1}p$

on calcule son espérance par la formule :

$\begin{equation*}\begin{split}\mathbb{E}\left(X\right) & = \sum_{k=1}^{\infty}k\thinspace\mathbb{P}\left(X=k\right)\\& = \frac{p}{1-p}\sum_{k=1}^{\infty}k\thinspace\left(1-p\right)^{k}\\& = \frac{p}{1-p}\thinspace\frac{1-p}{p^{2}}\\& = \frac{1}{p}\end{split}\end{equation*}$

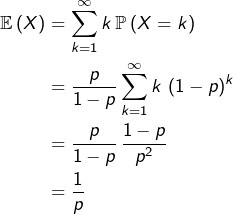
➡ Stratégie 2 : par dérivation

Tout repose sur le fait que :

$P_{n}\left(x\right)=x\thinspace\frac{d}{dx}\left(\sum_{k=0}^{n}x^{k}\right)$

En appliquant la formule $\left(\heartsuit\right)$ , il vient :

$\begin{eqnarray*}P_{n}\left(x\right) & = & x\thinspace\frac{d}{dx}\left(\frac{x^{n+1}-1}{x-1}\right)\\& = & x\thinspace\frac{\left(n+1\right)x^{n}\left(x-1\right)-\left(x^{n+1}-1\right)}{\left(x-1\right)^{2}}\end{eqnarray*}$

et l’on retrouve (heureusement) le résultat encadré plus haut, après simplification.

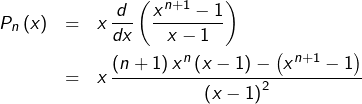
➡ Stratégie 3 : par interversion

On observe que :

$\begin{equation*}\begin{split}P_{n}\left(x\right) & = \sum_{k=1}^{n}\left(\sum_{i=1}^{k}x^{k}\right)\\& \underset{\star}{=} \sum_{i=1}^{n}\left(\sum_{k=i}^{n}x^{k}\right)\\& = \sum_{i=1}^{n}\frac{x^{i}-x^{n+1}}{1-x}\\& = \frac{1}{1-x}\left(\sum_{i=1}^{n}x^{i}\right)-\frac{nx^{n+1}}{1-x}\end{split}\end{equation*}$

l’égalité $(\star)$ résultant de l’interversion des sommes sur un domaine triangulaire (voir cet article). Et donc :

$\begin{equation*}\begin{split}P_{n}\left(x\right) & = \frac{1}{1-x}\left(\frac{x-x^{n+1}}{1-x}-nx^{n+1}\right)\end{split}\end{equation*}$

et il ne reste qu’à simplifier.

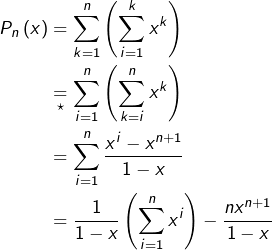
➡ Stratégie 4 : par équation

L’astuce est la suivante. On écrit artificiellement :

$\begin{equation*}\begin{split}P_{n}\left(x\right) & = \sum_{k=1}^{n}\left[\left(k+1\right)x^{k}-x^{k}\right]\\& = \frac{1}{x}\left(\sum_{k=2}^{n+1}kx^{k}\right)-\frac{x-x^{n+1}}{1-x}\end{split}\end{equation*}$

d’où l’équation vérifiée par $P_{n}\left(x\right)$ :

$P_{n}\left(x\right)=\frac{1}{x}\left(P_{n}\left(x\right)+\left(n+1\right)x^{n+1}-x\right)-\frac{x-x^{n+1}}{1-x}$

On en déduit :

$\left(\frac{1}{x}-1\right)P_{n}\left(x\right)=\frac{x-\left(n+1\right)x^{n+1}}{x}+\frac{x-x^{n+1}}{1-x}$

et il ne reste qu’à simplifier.

7 – Une somme trigonométrique

Pour tout couple $\left(n,\theta\right)$ formé d’un entier $n\geqslant1$ et d’un réel $\theta,$ considérons la somme :

$A_{n}\left(\theta\right)=\sum_{k=1}^{n}\cos\left(k\theta\right)$

et cherchons à la calculer explicitement (contrairement aux apparences, cette question n’a rien d’artificiel : elle apparaît naturellement dans l’étude des séries de Fourier et tout particulièrement du noyau de Dirichlet).

Cette expression ne se présente pas sous les traits d’une somme géométrique… mais presque :

Observation-clef

L’expression $A_{n}\left(\theta\right)$ peut être vue comme la partie
réelle d’une somme géométrique.

Posons en effet :

$Z_{n}\left(\theta\right)=\sum_{k=1}^{n}e^{ik\theta}$

de sorte que $A_{n}\left(\theta\right)=\text{Re}\left(Z_{n}\left(\theta\right)\right).$ Selon la formule de Moivre :

$Z_{n}\left(\theta\right)=\sum_{k=1}^{n}\left(e^{i\theta}\right)^{k}$

ce qui montre bien qu’il s’agit d’une somme géométrique de raison $e^{i\theta}.$

Si $\theta$ est multiple de $2\pi,$ alors $e^{i\theta}=1$ et donc $Z_{n}\left(\theta\right)=n.$

Supposons maintenant que $\theta$ n’est pas multiple de $2\pi.$ Alors $e^{i\theta}\neq1$ et la formule $\left(\star\star\right)$ s’applique (avec $p=1)$ :

$Z_{n}\left(\theta\right)=\frac{e^{i\theta}-e^{i\left(n+1\right)\theta}}{1-e^{i\theta}}$

Il est judicieux d’équilibrer les exposants :

$Z_{n}\left(\theta\right)=e^{i\left(n+1\right)\theta/2}\thinspace\frac{e^{-in\theta/2}-e^{in\theta/2}}{e^{-i\theta/2}-e^{i\theta/2}}$

ce qui donne finalement, via la formule d’Euler pour le sinus :

$Z_{n}\left(\theta\right)=e^{i\left(n+1\right)\theta/2}\thinspace\frac{\sin\left(\frac{n\theta}{2}\right)}{\sin\left(\frac{\theta}{2}\right)}$

Il est à présent clair que :

$A_{n}\left(\theta\right)=\frac{\sin\left(\frac{n\theta}{2}\right)\cos\left(\frac{\left(n+1\right)\theta}{2}\right)}{\sin\left(\frac{\theta}{2}\right)}$

Selon le contexte, il peut être opportun de linéariser le numérateur de cette dernière fraction, via la transformation

$\sin\left(a\right)\cos\left(b\right)=\frac{1}{2}\left[\sin\left(a+b\right)+\sin\left(a-b\right)\right]$

ce qui donne l’expression alternative :

$A_{n}\left(\theta\right)=\frac{\sin\left(\left(n+\frac{1}{2}\right)\theta\right)}{2\sin\left(\frac{\theta}{2}\right)}-\frac{1}{2}$

Résumons :

$\fcolorbox{black}{myBlue}{$\forall n\in\mathbb{N}^{\star},\thinspace\forall\theta\in\mathbb{R},\thinspace\displaystyle\sum_{k=1}^{n}\cos\left(k\theta\right)=\left\{ \begin{array}{cc}\dfrac{\sin\left(\left(n+\frac{1}{2}\right)\theta\right)}{2\sin\left(\frac{\theta}{2}\right)}-\dfrac{1}{2} & \text{si }\theta\notin2\pi\mathbb{Z}\\\\n & \text{sinon}\end{array}\right.$}$

L’idée principale qui a mené à cette formule est à retenir : considérer cette somme comme la partie réelle d’une somme géométrique.

Vous pourrez obtenir une formule similaire pour la somme 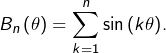${\displaystyle B_{n}\left(\theta\right)=\sum_{k=1}^{n}\sin\left(k\theta\right)}.$ Cette question est abordée à l’exercice n° 4 de cette fiche.

8 – Une famille de séries alternées

Posons pour tout $q\in\mathbb{N}^{\star}$ :

$\sigma_{q}=\sum_{k=0}^{\infty}\frac{\left(-1\right)^{k}}{qk+1}$

Le théorème des séries alternées garantit l’existence des nombres $\sigma_{q}$ puisque, pour tout $q\in\mathbb{N}^{\star},$ la suite $\left(\frac{1}{qk+1}\right)_{k\geqslant0}$ décroît et converge vers 0.

Dans cette section, nous n’allons pas seulement établir l’existence des $\sigma_{q}$ . Nous allons surtout en donner une expression intégrale sans RIEN n’avoir à connaître sur les séries numériques.

L’ingrédient principal de ce qui va suivre est, vous vous en doutez, une somme géométrique …

Introduisons une suite d’applications $\left(S_{n}\right)_{n\geqslant1}$ définies sur $\left[0,1\right]$ par :

$S_{n}\left(t\right)=\sum_{k=0}^{n-1}\left(-1\right)^{k}t^{qk}$

et intégrons $S_{n}$ sur $\left[0,1\right].$ Par linéarité de l’intégrale :

$\int_{0}^{1}S_{n}\left(t\right)\thinspace dt=\sum_{k=0}^{n-1}\left(-1\right)^{k}\int_{0}^{1}t^{qk}\thinspace dt=\sum_{k=0}^{n-1}\frac{\left(-1\right)^{k}}{qk+1}=\sigma_{q}$

Par ailleurs, la formule $\left(\star\right)$ nous dit que, pour tout $t\in\left[0,1\right]$ :

$S_{n}\left(t\right)=\sum_{k=0}^{n-1}\left(-t^{q}\right)^{k}=\frac{1-\left(-t^{q}\right)^{n}}{1+t^{q}}$

de sorte que :

$\int_0^1S_{n}\left(t\right)\,dt=\int_{0}^{1}\frac{1}{1+t^{q}}\thinspace dt-R_{n}\qquad\text{avec }R_{n}=\left(-1\right)^{n}\int_{0}^{1}\frac{t^{qn}}{1+t^{q}}\thinspace dt$

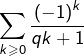Si l’on prouve que $\lim_{n\rightarrow\infty}R_{n}=0,$ il en résultera la convergence de la série $\sum_{k\geqslant0}\frac{\left(-1\right)^{k}}{qk+1}$ et la formule :

$\boxed{\sigma_{q}=\int_{0}^{1}\frac{1}{1+t^{q}}\thinspace dt}$

Or c’est facile à voir, puisque :

$\left|R_{n}\right|=\int_{0}^{1}\frac{t^{qn}}{1+t^{q}}\thinspace dt\leqslant\int_{0}^{1}t^{qn}\thinspace dt=\frac{1}{qn+1}\underset{n\rightarrow\infty}{\rightarrow}0$

A titre d’exemple, détaillons les cas particuliers $q=1,$ $q=2$ et $q=3.$

Les deux premiers sont immédiats; on obtient les formules célèbres :

$\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k=0}^{\infty}\frac{\left(-1\right)^{k}}{k+1}=\ln\left(2\right)}$}\qquad\text{et}\qquad\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k=0}^{\infty}\frac{\left(-1\right)^{k}}{2k+1}=\frac{\pi}{4}}$}$

Le troisième est un peu moins classique.

Pour calculer explicitement $\sigma_{3},$ commençons par décomposer la fraction rationnelle $\frac{1}{X^{3}+1}$ en éléments simples. On obtient aisément :

$\frac{1}{X^{3}+1}=\frac{1}{3\left(X+1\right)}+\frac{-X+2}{3\left(X^{2}-X+1\right)}$

Ensuite, il faut calculer :

$\alpha=\int_{0}^{1}\frac{1}{t+1}\thinspace dt=\ln\left(2\right)$

puis :

$\begin{equation*}\begin{split}\beta & = \int_{0}^{1}\frac{-t+2}{t^{2}-t+1}\thinspace dt\\& = \int_{0}^{1}\frac{-t+2}{\left(t-\frac{1}{2}\right)^{2}+\frac{3}{4}}\thinspace dt\\& = \int_{-1/2}^{1/2}\frac{-s+\frac{3}{2}}{s^{2}+\frac{3}{4}}\thinspace ds\\& = \left[-\frac{1}{2}\ln\left(s^{2}+\frac{3}{4}\right)+\sqrt{3}\arctan\left(\frac{2s}{\sqrt{3}}\right)\right]_{-1/2}^{1/2}\\& = 2\sqrt{3}\arctan\left(\frac{1}{\sqrt{3}}\right)\\& = \frac{\pi\sqrt{3}}{3}\end{split}\end{equation*}$

d’où l’on tire finalement $\sigma_{3}=\frac{1}{3}\left(\alpha+\beta\right),$ c’est-à-dire :

$\fcolorbox{black}{myBlue}{$\displaystyle{\sum_{k=0}^{\infty}\frac{\left(-1\right)^{k}}{3k+1}=\frac{1}{3}\ln\left(2\right)+\frac{\pi\sqrt{3}}{9}}$}$

Annexe – Une montagne de sucre

Adoptons les notations suivantes :

$v$ = le volume d’un morceau de sucre,
$N$ = le nombre de morceaux de sucre,
$R$ = le rayon de la terre,
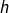$h$ = la hauteur de la couche de sucre.

Alors :

$\boxed{Nv=\frac{4}{3}\pi\left[\left(R+h\right)^{3}-R^{3}\right]}$

ce qui montre que $h$ est solution de l’équation du troisième degré suivante :

$x^{3}+3Rx^{2}+3R^{2}x-\frac{3Nv}{4\pi}=0$

Comme $x\mapsto\left(R+x\right)^{3}$ est strictement croissante, cette équation possède une unique solution réelle.

Les données numériques sont (en arrondissant légèrement) :

$N=1.7\times10^{30},\qquad v=1\;cm^{3}=10^{-6}\;m^{3},\qquad R=6\thinspace371\;km=6\thinspace371\thinspace000\;m$

Avec l’aide d’un logiciel adéquat, on obtient :

$h\simeq0.67\times10^{8}$

Bien sûr, ce résultat est exprimé en mètres.

Il faudrait donc recouvrir la terre d’une couche haute d’environ 67 000 km. Je ne sais pas si vous voyez le truc … Cette altitude est supérieure à dix fois le rayon terrestre. Elle n’est pas très éloignée de l’altitude de l’orbite géostationnaire, soit à peu près 1/6 de la distance terre-lune !!

Le titre de la section 2 a donc été mal choisi. Il aurait fallu opter pour quelque chose comme « une quantité astronomique de sucre ! ».

Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Partager cet article

Cet article a 2 commentaires

Oncle_Junior 10 Nov 2022 Répondre

Bonjour Monsieur,
Merci pour cet article !
Dans la section 8, après « de sorte que » il me semble qu’il manque le signe intégrale devant Sn (et plus bas dans la calcul de bêta, les bornes -1/2 et 1/2 s’affichent mal pour la primitive entre crochets, mais cela est pê du à l’affichage sur smartphone !).
Bien à vous
1. René Adad 11 Nov 2022 Répondre
  
  … et merci de m’avoir signalé ces fautes de frappes. J’ai fait les rectifications nécessaire.