Solution pour le challenge n° 37

Solution pour le challenge 37

Etant donné une couple $\left(a,b\right)$ de nombres réels, on sait (formule d’addition du sinus) que :
$\displaystyle{\sin\left(a+b\right)=\sin\left(a\right)\cos\left(b\right)+\cos\left(a\right)\sin\left(b\right)}$

D’après l’inégalité triangulaire et vu que $\vert\cos(t)\vert\leqslant1$ pour tout $t\in\mathbb{R}$ , il s’ensuit que :

Une récurrence immédiate montre alors que, pour tout $n\in\mathbb{N}^{\star}$ et pour tout $\left(x_{1},\cdots,x_{n}\right)\in\mathbb{R}^{n}$ :

$\left|\sin\left(\sum_{k=1}^{n}x_{k}\right)\right|\leqslant\sum_{k=1}^{n}\left|\sin\left(x_{k}\right)\right|\quad\left(\star\right)$

Posons maintenant 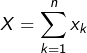$\displaystyle{X=\sum_{k=1}^{n}x_{k}}$ .

D’après $\left(\star\right)$ :

$\begin{eqnarray*}& &\sum_{k=1}^{n}\left|\sin\left(x_{k}\right)\right|+\left|\cos\left(\sum_{k=1}^{n}x_{k}\right)\right|\\& \geqslant & \left|\sin\left(X\right)\right|+\left|\cos\left(X\right)\right|\\& \geqslant & \sin^{2}\left(X\right)+\cos^{2}\left(X\right)=1\end{eqnarray*}$

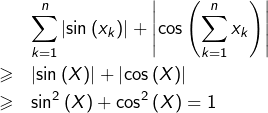
comme souhaité.

Pour consulter l’énoncé, c’est ici

Partager cet article

Laisser un commentaire Annuler la réponse