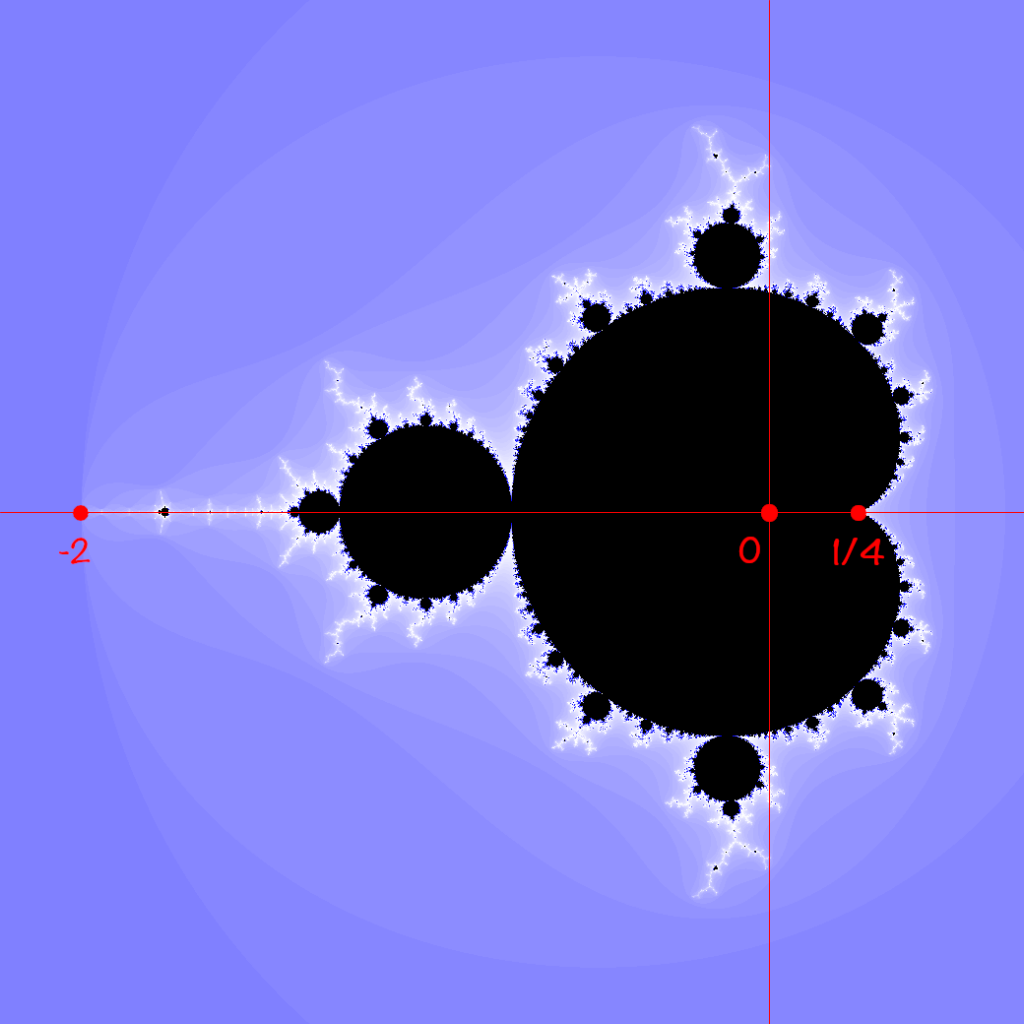
L’ensemble de Mandelbrot, noté ![]() , a été défini au début de cet article.
, a été défini au début de cet article.
L’objet de ce qui suit est de prouver le résultat élémentaire suivant :
Proposition
La trace sur ![]() de l’ensemble de Mandelbrot :
de l’ensemble de Mandelbrot : ![]()
D’après le lemme d’évasion, on sait que si ![]() alors
alors ![]() et donc
et donc ![]() Par conséquent
Par conséquent ![]() et en particulier :
et en particulier : ![]() .
.
De plus, on voit facilement que si ![]() , alors la suite définie par :
, alors la suite définie par :
![]()
![]()
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{M\cap\mathbb{R}\subset\left[-2,\dfrac{1}{4}\right]}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5010b2c410bf8fbc3866c410b72bdb81_l3.png)
Prouvons à présent l’inclusion inverse.
Pour tout ![]() l’application
l’application ![]() possède deux points fixes (confondus en
possède deux points fixes (confondus en ![]() lorsque
lorsque ![]() à savoir :
à savoir :
![]()
- si
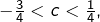 alors
alors 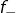 est attractif puisque
est attractif puisque 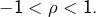
- si
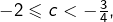 alors
alors  est répulsif car
est répulsif car 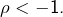
- et pour
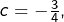 le point fixe
le point fixe 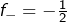 est indifférent car
est indifférent car 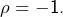
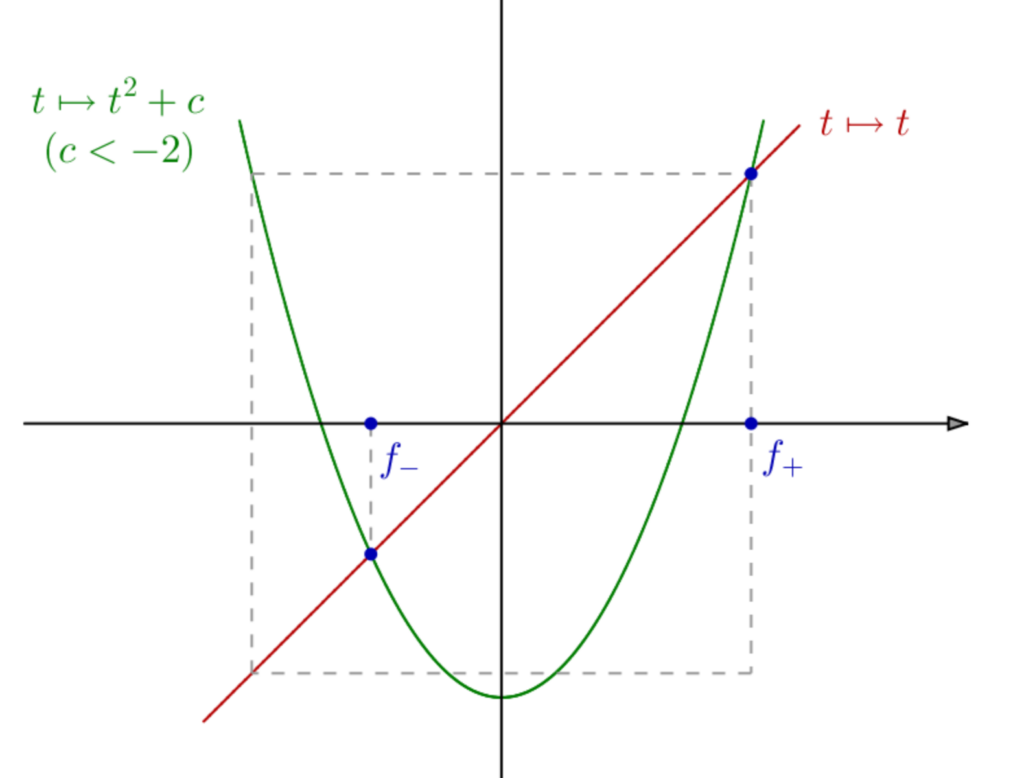
Le point important est que l’intervalle ![]() est stable par
est stable par ![]()
En effet, si ![]() alors :
alors :
![]()
![]()
Détails
On résout, pour ![]() l’inéquation
l’inéquation ![]() c’est-à-dire :
c’est-à-dire :
![]()
![]()
![]()
Comme ![]() la suite
la suite ![]() est bornée et donc
est bornée et donc ![]() Ainsi :
Ainsi :
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{M\cap\mathbb{R}\supset\left[-2,\dfrac{1}{4}\right]}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0242fa0bcf31dc341b25e73e76b64b19_l3.png)
Remarque
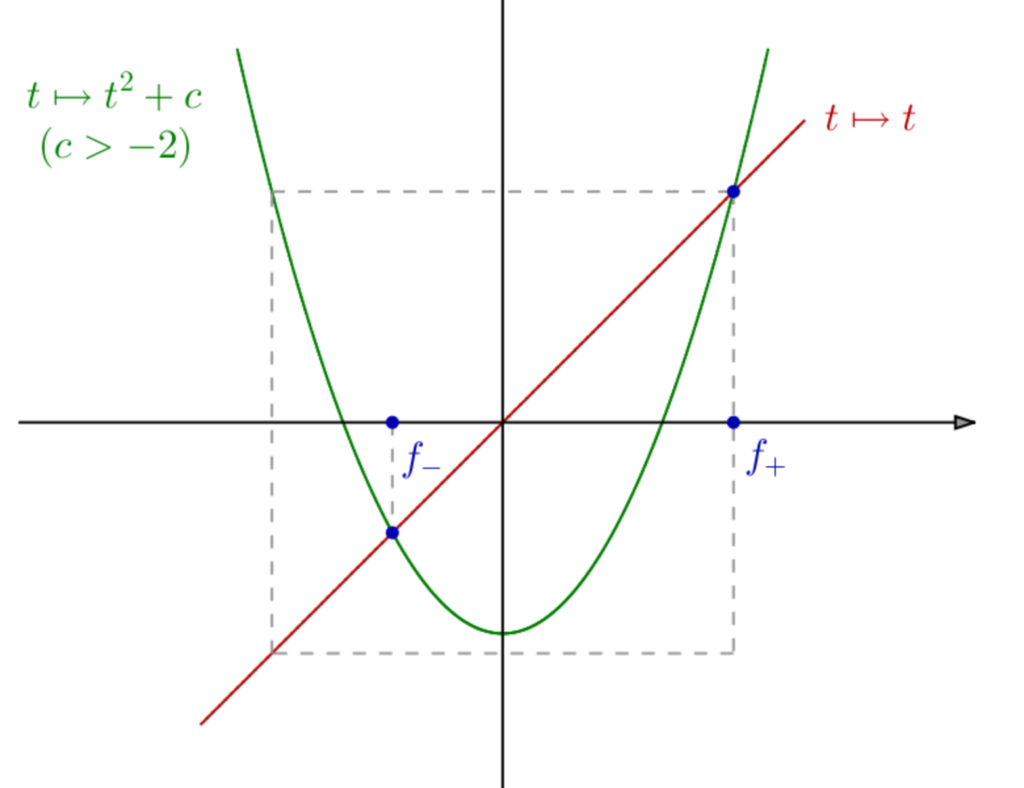
Si ![]() alors
alors ![]() n’est plus stable par
n’est plus stable par ![]() En effet :
En effet :
![]()
- pour
 légèrement inférieur à
légèrement inférieur à 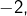
- pour
 légèrement supérieur à
légèrement supérieur à 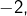
- pour
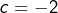 (le cas limite).
(le cas limite).


Un article intéressant
Merci
DR