Lettre B

BASE CANONIQUE

Si $E$ est un espace vectoriel abstrait de dimension finie $n\geqslant1,$ il n’existe pas parmi les bases de $E$ de base privilégiée.

En revanche, lorsque $E$ est explicitement identifié, on peut généralement distinguer une base plus naturelle, plus standard, que toute autre.

Cette base est appelée la base canonique de $E.$

➢ Par exemple, si $E=\mathbb{K}^{n}$ alors sa base canonique est $\left(e_{1},\cdots,e_{n}\right)$ où l’on a posé :

$\begin{eqnarray*}e_{1} & = & \left(1,0,0,\cdots,0,0\right)\\ e_{2} & = & \left(0,1,0,\cdots,0,0\right)\\ \vdots & & \vdots\\ e_{n} & = & \left(0,0,0,\cdots,0,1\right)\end{eqnarray*}$

➢ Autre exemple, si $E=\mathbb{K}_{n}\left[X\right]$ (espace de polynômes de degré inférieur ou égal à $n),$ alors sa base canonique est :

$\left(1,X,X^{2},\cdots,X^{n}\right)$

ce qui n’est au fond qu’une reformulation de la même chose, puisque par définition $X^{k}$

est la suite presque nulle :

$\left(0,0,0,\cdots0,1,0,\cdots\right)$

dans laquelle chaque terme est nul à l’exception du $k-$

ème, qui vaut 1 (attention : les termes de la suite sont numérotés à partir de l’indice 0).

Encore un, pour la route …

➢ Si $E=\mathcal{M}_{n,p}\left(\mathbb{K}\right)$ (espace des matrices rectangulaires à $n$ lignes et $p$ colonnes), alors sa base canonique est formée des matrices élémentaires :

$E_{r,s}=\left[\delta_{i,r}\delta_{j,s}\right]_{{1\leqslant i\leqslant n\atop 1\leqslant j\leqslant q}}$

avec $1\leqslant r\leqslant n,$

$1\leqslant s\leqslant p$

et où $\delta_{u,v}$

est le symbole de Kronecker.

Autrement dit, $E_{r,s}$ est la matrice dont tous les termes sont nuls à l’exception de celui situé à l’intersection de la ligne $r$ et de la colonne $s,$ qui vaut 1. On reconnaît encore la même idée.

Noter que l’ordre des vecteurs dans une base a son importance; il faut donc le préciser en cas de doute. Aucun doute pour les deux premiers exemples, mais les choses sont moins nettes pour les matrices élémentaires. On peut adopter par défaut l’ordre lexicographique sur les couples $\left(r,s\right)\in\left\llbracket 1,n\right\rrbracket \times\left\llbracket 1,p\right\rrbracket .$ Ainsi, dans le cas particulier où $n=2$ et $p=3$ , la base canonique de $\mathcal{M}_{2,3}\left(\mathbb{K}\right)$ sera :

$\left(E_{1,1},\,E_{1,2},\,E_{1,3},\,E_{2,1},\,E_{2,2},\,E_{2,3}\right)$

BERNOULLI (inégalité)

Proposition

Etant donné un réel $x\in\left]-1,0\right[\cup\left]0,+\infty\right[$ ainsi qu’un entier $n\geqslant2$ :

$\left(1+x\right)^{n}>1+nx$

On prouve ceci par récurrence. Pour $n=2,$ c’est immédiat puisque $x\neq0$ :

$\left(1+x\right)^{2}=1+2x+x^{2}>1+2x$

Ensuite, en supposant l’inégalité vraie pour un certain exposant $n\geqslant2$

$\begin{eqnarray*}\left(1+x\right)^{n+1} & = & \left(1+x\right)^{n}\left(1+x\right)\\& > & \left(1+nx\right)\left(1+x\right)\end{eqnarray*}$

d’après l’HR et parce que $1+x>0.$

Or :

$\left(1+nx\right)\left(1+x\right)=1+\left(n+1\right)x+nx^{2}>1+\left(n+1\right)x$

ce qui donne la conclusion.

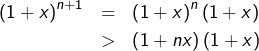
Remarque

Si $x>0,$ on peut aussi s’en sortir avec la formule du binôme :

$\left(1+x\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}x^{k}=1+nx+\sum_{k=2}^{n}\binom{n}{k}x^{k}$

Comme chacun des termes de cette dernière somme est strictement positif, on obtient l’inégalité voulue.

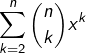En revanche, pour $x\in\left]0,1\right[$ , les termes cette somme sont de signe alterné et le signe de $\displaystyle{\sum_{k=2}^{n}\binom{n}{k}x^{k}}$ ne saute pas aux yeux.

BIJECTION

Une bijection d’un ensemble $E$ vers un ensemble $F$ est, en quelque sorte, une « correspondance parfaite » entre ces deux ensembles.

Intuitivement, cela signifie que :

de chaque élément de $E$ part une unique flèche vers un élément de $F$ ,
vers chaque élément de $F$ parvient une unique flèche provenant d’un élément de $E$ .

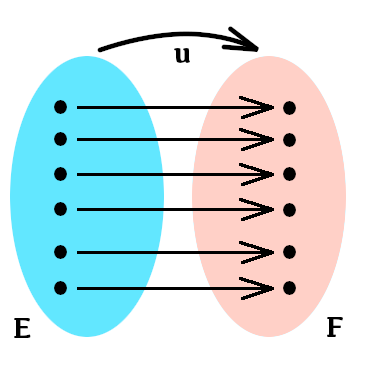
De manière précise, une bijection est une application $u:E\to F$ à la fois injective et surjective.

➢ L’injectivité signifie que tout élément de $F$ possède au plus un antécédent par $u$ .

➢ La surjectivité signifie que tout élément de $F$ possède au moins un antécédent par $u$ .

La superposition des deux conditions signifie que tout élément de $F$ possède un unique antécédent par $u$ . En symboles :

$\forall y\in F,\exists !x\in E;\,u(x)=y$

Chacune des applications suivantes est un exemple de bijection :

$f:\{0,1,2\}\to\{0,2,4\},n\mapsto 2n$

$g:\mathbb{N}\to\mathbb{N}^\star,n\mapsto n+1$

$h:\mathbb{N}\to\mathbb{Z},n\mapsto\left\{\begin{matrix}\frac{n}{2} & \text{si }n\text{ est pair}\\\\-\frac{n+1}{2} & \text{sinon}\end{matrix}\right.$

S’il existe une bijection $u:E\to F$ , alors il existe une bijection de $v:F\to E$ (à commencer par la bijection réciproque de $u$ , notée $u^{-1}$ , qui a tout élément de $F$ associe son unique antécédent par $u$ ). On peut donc parler d’ensembles « en bijection », sans préciser d’ensemble de départ ni d’arrivée : deux tels ensembles sont dits équipotents. Dans le cas de deux ensembles finis, cela signifie simplement que les deux ensembles ont le même cardinal.

Les exemples ci-dessus montrent que $\mathbb{N}^\star$ et $\mathbb{Z}$ sont équipotents à $\mathbb{N}$ . On peut montrer que c’est aussi le cas de $\mathbb{Q}$ : pour cette raison, $\mathbb{N}$ , $\mathbb{N}^\star$ et $\mathbb{Q}$ sont dits dénombrables. On peut montrer que $\mathbb{R}$ , en revanche, n’est pas dénombrable.

BINOMIAUX (coefficients)

Si $n,k$ sont deux entiers naturels, on note $\binom{n}{k}$ le nombre de parties de cardinal $k$ dans un ensemble de cardinal $n.$

Cet entier est évidemment nul si $k>n.$ Et sinon, on peut montrer que :

$\binom{n}{k}=\frac{n!}{k!\left(n-k\right)!}$

Si $1\leqslant k\leqslant n,$

cette formule peut s’écrire, après simplification par $\left(n-k\right)!$

$\binom{n}{k}=\frac{n\left(n-1\right)\cdots\left(n-k+1\right)}{k!}$

Les entiers $\binom{n}{k}$

sont appelés coefficients binomiaux, car ils interviennent dans la célèbre formule du binôme de Newton :

$\left(a+b\right)^{n}=\sum_{k=0}^{n}\binom{n}{k}a^{n-k}b^{k}$

formule dans laquelle $a,b$

sont deux nombres complexes.

Plus généralement, cette égalité reste valable dans un anneau, pour tout couple $\left(a,b\right)$ d’éléments qui commutent. On peut notamment l’appliquer à une couple de matrices carrées de même taille, à coefficients dans un même corps $\mathbb{K}$ .

Il existe de nombreuses formules faisant intervenir les coefficients binomiaux. Quelques unes des plus importantes son détaillées dans cet article.

Les coefficients binomiaux généralisés sont définis, pour tout $\left(\alpha,k\right)\in\mathbb{R}\times\mathbb{N},$ par :

$\binom{\alpha}{k}=\frac{\alpha\left(\alpha-1\right)\cdots\left(\alpha-k+1\right)}{k!}$

On peut montrer que :

$\forall t\in\left]-1,1\right[,\:\left(1+t\right)^{\alpha}=\sum_{k=0}^{\infty}\binom{\alpha}{k}t^{k}$

BOLZANO-WEIERSTRASS (théorème de)

Une suite réelle $\left(x_{n}\right)_{n\in\mathbb{N}}$ ne possède pas nécessairement de valeurs d’adhérence, comme on le voit en considérant la suite croissante des entiers naturels.

C’est toutefois le cas si la suite considérée est supposée bornée. Ce résultat constitue le théorème de Bolzano-Weierstrass.

En voici deux esquisses de preuve …

1 – Par dichotomie. Par hypothèse, il existe des réels $a<b$ tels que $x_n\in\left[a,b\right]$ pour tout $n\in\mathbb{N}.$ Notons $m=\frac{a+b}{2}.$ L’un au moins des deux segments $\left[a,m\right]$ ou $\left[m,b\right]$ contient $x_{n}$ pour une infinité d’indices $n$ (tout simplement parce que l’union de deux ensembles finis est un ensemble fini !). En répétant cet argument, on construit par récurrence une suite $\left(S_{k}\right)_{k\geqslant0}$ de segments tels que :

$\forall k\in\mathbb{N},\;S_{k+1}\subset S_{k},$
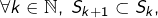
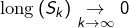$\text{long}\left(S_{k}\right)\underset{k\rightarrow\infty}{\rightarrow}0$ (plus précisément : $\text{long}\left(S_{k}\right)=\frac{b-a}{2^{k}})$ ,
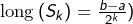l’ensemble 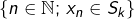$\left\{ n\in\mathbb{N};\thinspace x_{n}\in S_{k}\right\}$ est infini pour tout $k$ .

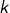La propriété des segments emboîtés s’applique et montre que $\bigcap_{k=0}^{\infty}S_{k}$ est un singleton $\left\{ \lambda\right\} .$

On vérifie que $\lambda$ est la limite d’une suite extraite de $\left(x_{n}\right)_{n\geqslant0},$ autrement dit : une valeur d’adhérence de cette suite.

2 – Via le lemme des pics. Ce résultat un peu technique dit que de toute suite réelle, on peut extraire une sous-suite monotone. Il fait l’objet de l’exercice n° 9 de cette fiche. On se donne alors une suite réelle bornée; on en extrait (grâce au lemme des pics) une sous-suite monotone, qui est évidemment bornée donc convergente (d’après le théorème de la limite monotone).

On peut aussi voir les choses de plus haut : le théorème de Bolzano-Weierstrass exprime la compacité séquentielle relative des parties bornées de $\mathbb{R}.$

Si l’on considère plus généralement une suite $\left(x_{n}\right)_{n\geqslant0}$ à termes dans un espace métrique, alors l’ensemble de ses valeurs d’adhérence est :

$V=\bigcap_{n=0}^{\infty}\overline{X_{n}}$

où $X_{n}$

désigne l’ensemble $\left\{ x_{k};\thinspace k\geqslant n\right\} .$

On voit ainsi que $V$ est fermé (en tant qu’intersection d’une famille de fermés).

Maintenant, si la suite considérée est à termes dans un espace vectoriel normé de dimension finie, alors $V$ apparaît comme l’intersection d’une suite décroissante de compacts non vides, ce qui prouve que $V\neq\emptyset.$

BORNÉ

La notion de partie bornée est présentée ici dans $\mathbb{R}$ par souci de simplicité. Son cadre naturel est celui des espaces métriques.

On dit qu’une partie $B$ de $\mathbb{R}$ est bornée lorsque :

$\exists M\in\mathbb{R}^{+},\thinspace\forall x\in B,\thinspace\left|x\right|\leqslant M$

Il revient au même d’affirmer qu’il existe deux réels $a,b$

tels que $a<b$

et $B\subset\left[a,b\right].$

Il est facile de voir que :

l’intersection d’une famille de parties bornées est bornée.
l’union d’une famille finie de parties bornées est bornée.

Parmi les parties bornées de $\mathbb{R},$ on peut distinguer :

les intervalles bornés. Ce sont ceux de l’une des formes suivantes :
$\emptyset,\:\left\{ a\right\} ,\:\left[a,b\right],\:\left[a,b\right[,\:\left]a,b\right],\:\left]a,b\right[$
les parties fermées et bornées. Pour une telle partie 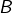$B$ , on peut extraire de toute suite 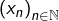$\left(x_{n}\right)_{n\in\mathbb{N}}$ à termes dans 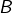$B$ une sous-suite convergente dont la limite appartient à 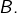$B.$ La réciproque est vraie : toute partie de $\mathbb{R}$ ayant cette propriété est fermée et bornée. En d’autres termes, les parties fermées et bornées de $\mathbb{R}$ sont exactement les parties compactes de $\mathbb{R}$ .

A l’intersection des deux catégories 1 et 2 ci-dessus, on trouve les segments (intervalles fermés et bornés).

Maintenant, si $D\subset\mathbb{R}$ alors une application $f:D\rightarrow\mathbb{R}$ est dite bornée lorsque $f\left\langle D\right\rangle$ est une partie bornée au sens précédent. Cela signifie donc qu’il existe $M\in\mathbb{R}^{+}$ tel que :

$\forall x\in D,\thinspace\left|f\left(x\right)\right|\leqslant M$

Partager cet article