
1 – Le principe d’inclusion / exclusion
![]()
![]()
A présent, passons au cas général …
Théorème 1 (« formule du crible » ou « de Poincaré » ou « principe d’inclusion-exclusion »)
![]()
![Rendered by QuickLaTeX.com \[\boxed{\#\bigcup_{i=1}^{n}A_{i}=\sum_{k=1}^{n}\left(-1\right)^{k-1}S_{k}}\qquad\left(\star\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1ffbc5c407a8e892812dd3752aca7ad8_l3.png)
Remarque 1
![]()
![]()
![]()
![]()
![]()
Remarque 2
Revenons à n quelconque.
L’entier ![]() est la somme des cardinaux des intersections
est la somme des cardinaux des intersections ![]() à
à ![]() des
des ![]() En particulier :
En particulier :
![Rendered by QuickLaTeX.com \[S_{1}=\sum_{i=1}^{n}\#A_{i}\qquad\text{et}\qquad S_{n}=\#\bigcap_{i=1}^{n}A_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa2e8f600ae3513cf0deb41def70d9ed_l3.png)
Noter que la somme qui définit ![]() comporte
comporte ![]() termes.
termes.
Pour une preuve de la formule du crible, voir plus bas : le corollaire qui suit la preuve du Lemme 3.
2 – Des égalités tronquées qui deviennent inégalités
On va maintenant prouver que si, dans l’égalité ![]() , le second membre est « tronqué », c’est-à-dire si l’on n’en conserve que les
, le second membre est « tronqué », c’est-à-dire si l’on n’en conserve que les ![]() premiers termes (pour un certain
premiers termes (pour un certain ![]() ), alors on obtient une inégalité. Plus précisément :
), alors on obtient une inégalité. Plus précisément :
Théorème 2 (inégalités de Bonferroni)
Si ![]() sont des ensembles finis, alors :
sont des ensembles finis, alors :
![Rendered by QuickLaTeX.com \[\forall j\in\llbracket1,n\rrbracket,\:\left\{ \begin{matrix}{\displaystyle \#\bigcup_{i=1}^{n}A_{i}\geqslant\sum_{k=1}^{j}\left(-1\right)^{k-1}S_{k}} & & \text{si }j\text{ est pair}\\\\{\displaystyle \#\bigcup_{i=1}^{n}A_{i}\leqslant\sum_{k=1}^{j}\left(-1\right)^{k-1}S_{k}} & & \text{si }j\text{ est impair}\end{matrix}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c2a3c361d0219889ea62f7bf9c453d9e_l3.png)
Ces inégalités peuvent être formulées en termes de probabilités.
C’est ainsi que le mathématicien italien Carlo Emilio BONFERRONI (1892 – 1960) les publia en 1935, sous une forme appliquée à un problème d’assurance-vie (!), puis en 1936 dans un style plus abstrait.

Le cas particulier ![]() est très classique :
est très classique :
Théorème 3 (inégalité de Boole)
Si ![]() sont des ensembles finis, alors :
sont des ensembles finis, alors :
![Rendered by QuickLaTeX.com \[\#\bigcup_{i=1}^{n}A_{i}\leqslant\sum_{i=1}^{n}\#A_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2980da0632d007764994a632c4b69198_l3.png)
Preuve (cliquer pour déplier / replier)
On prouve aisément ceci par récurrence.
Pour ![]() , il n’y a rien à démontrer. Pour
, il n’y a rien à démontrer. Pour ![]() , on sait que :
, on sait que :
![]()
![Rendered by QuickLaTeX.com \[\#\bigcup_{i=1}^{n+1}A_{i}=\#\left[\left(\bigcup_{i=1}^{n}A_{i}\right)\cup A_{n+1}\right]\leqslant\#\bigcup_{i=1}^{n}A_{i}+\#A_{n+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-73d391dfcc1932993830495aad894c66_l3.png)
On conclut avec l’hypothèse de récurrence.

Pour traiter le cas général (théorème 2), on aura besoin de quelques résultats préliminaires, rassemblés dans la section suivante.
3 – Trois lemmes techniques
Lemme 1
Soient ![]() des réels positifs (avec
des réels positifs (avec ![]() ). On suppose qu’il existe
). On suppose qu’il existe ![]() tel que
tel que ![]() soit croissante et
soit croissante et ![]() soit décroissante. Si de plus :
soit décroissante. Si de plus :
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{n}\left(-1\right)^{i}a_{i}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7934ccdd505abb0c51a8794b6a0d3d48_l3.png)
![Rendered by QuickLaTeX.com \[\left\{ \begin{matrix}{\displaystyle \sum_{i=0}^{j}\left(-1\right)^{i}a_{i}\geqslant0} & & \text{si }j\text{ est pair}\\\\{\displaystyle \sum_{i=0}^{j}\left(-1\right)^{i}a_{i}\leqslant0} & & \text{si }j\text{ est impair}\end{matrix}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b19dc80473a05de0bf91f1078b5c0e7d_l3.png)
Preuve (cliquer pour déplier / replier)
Supposons ![]() .
.
➡ Si ![]() est pair, alors en posant
est pair, alors en posant ![]() :
:
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{2q}\left(-1\right)^{i}a_{i}=a_{0}+\sum_{i=1}^{q}\left(a_{2i}-a_{2i-1}\right)\geqslant0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4c5ca2c081ac5b128be7939550c2c702_l3.png)
➡ Si
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{2q+1}\left(-1\right)^{i}a_{i}=\sum_{i=0}^{q}\left(a_{2i}-a_{2i+1}\right)\leqslant0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1fc832beb8f6631925fbc97744285fa0_l3.png)
Supposons maintenant ![]() . On constate que :
. On constate que :
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{j}\left(-1\right)^{i}a_{i}=\underbrace{\sum_{i=0}^{n}\left(-1\right)^{i}a_{i}}_{=0}-\sum_{i=j+1}^{n}\left(-1\right)^{i}a_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6e99da4bff1decea401e86dc732ba627_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{j}\left(-1\right)^{i}a_{i}=-\sum_{\ell=0}^{n-j-1}\left(-1\right)^{n-\ell}a_{n-\ell}=\left(-1\right)^{n-1}\sum_{\ell=0}^{n-j-1}\left(-1\right)^{\ell}a_{n-\ell}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2beb3571be47c3e0e32be551d5f5617a_l3.png)
La dernière somme est du signe de ![]() , donc
, donc 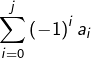 est du signe de
est du signe de ![]() .
.
Corollaire (Application du Lemme 1 aux coefficients binomiaux)
Pour ![]() donné, la suite finie de terme général
donné, la suite finie de terme général ![]() (pour
(pour ![]() ) est d’abord croissante, jusqu’au terme d’indice
) est d’abord croissante, jusqu’au terme d’indice ![]() , puis décroissante.
, puis décroissante.
De plus :
![Rendered by QuickLaTeX.com \[\sum_{i=0}^{n}\left(-1\right)^{i}\binom{n}{i}=\left(1-1\right)^{n}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-72b60a4f39f36b5d7f7751686ac4b879_l3.png)
Donc, en appliquant le lemme précédent :
![Rendered by QuickLaTeX.com \[\forall j\in\llbracket0,n-1\rrbracket,\:\left(-1\right)^{j}\sum_{i=0}^{j}\left(-1\right)^{i}\binom{n}{i}\geqslant0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a6a4d36002292684567eeacc65fd65f0_l3.png)
![Rendered by QuickLaTeX.com \[\forall j\in\llbracket0,n-1\rrbracket,\:\sum_{i=0}^{j}\left(-1\right)^{i}\binom{n}{i}=\left(-1\right)^{j}\binom{n-1}{j}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7de5bb6c6e69ccb075c8566f326ad03e_l3.png)
Lemme 2
![]()
![]()
Alors, pour tout ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\sum_{1\leqslant i_{1}<\cdots<i_{k}\leqslant n}\mathds{1}_{A_{i_{1}}\cap\cdots\cap A_{i_{k}}}\left(x\right)=\binom{\theta\left(x\right)}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3358e3dd6c3f1eb2db8e6e5b29bae8b8_l3.png)
Preuve (cliquer pour déplier / replier)
En notant ![]() , on voit que :
, on voit que :
![]()
où
![Rendered by QuickLaTeX.com \[\sum_{1\leqslant i_{1}<\cdots<i_{k}\leqslant n}\mathds{1}_{A_{i_{1}}\cap\cdots\cap A_{i_{k}}}\left(x\right)=\# {\mathcal{P}}_k\left(I\right)=\binom{\#I}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6aa52e91da45ac5ba5cb265ebf67c21e_l3.png)
et le résultat en découle puisque ![]() .
.
Lemme 3
Soient ![]() des ensembles
des ensembles ![]() et
et ![]() un ensemble contenant chacun des
un ensemble contenant chacun des ![]() .
.
Alors, la fonction indicatrice de l’union des ![]() est donnée par :
est donnée par :
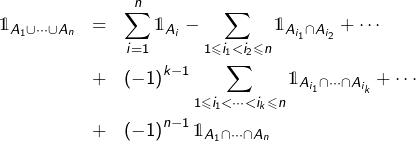
Preuve (cliquer pour déplier / replier)
Pour tout ![]() :
:

donc :
![Rendered by QuickLaTeX.com \[1-\prod_{i=1}^{n}\left(1-\mathds{1}_{A_{i}}\left(x\right)\right)=\mathds{1}_{A_{1}\cup\cdots\cup A_{n}}\left(x\right)\qquad\left(\star\star\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-50f42c88382c15f87823843297b269d4_l3.png)
Par ailleurs, on connaît la formule de développement d’un polynôme unitaire scindé (ici, à coefficients entiers, mais plus généralement à coefficients dans un anneau commutatif) :
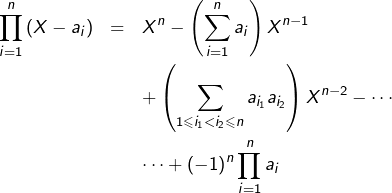
En remplaçant, pour chaque ![]() , le coefficient
, le coefficient ![]() par
par ![]() et en évaluant l’identité polynomiale en 1, on obtient :
et en évaluant l’identité polynomiale en 1, on obtient :
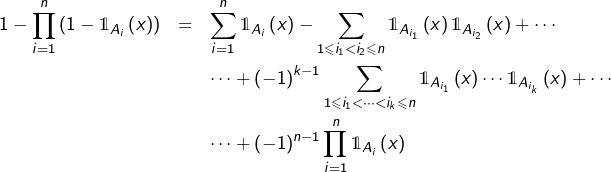
d’où le résultat, d’après ![]() .
.
Corollaire
En passant aux cardinaux dans l’égalité établie au lemme 3 (ce qui suppose bien sûr que les ensembles en présence soient tous finis) on obtient la formule du crible.
4 – Où l’on assemble les pièces du puzzle
Nous prouvons maintenant le théorème 2. Pour cela, reprenons les notations du théorème 1 et posons, pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[a_{j}=\#\bigcup_{i=1}^{n}A_{i}-\left[\sum_{k=1}^{j}\left(-1\right)^{k-1}S_{k}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a1891bac67523c9fc6306a4eea5e28ab_l3.png)
D’après le lemme 2, en notant toujours
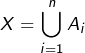 et en intervertissant deux sommes :
et en intervertissant deux sommes : ![Rendered by QuickLaTeX.com \[a_{j}=\sum_{x\in X}\left[1-\sum_{k=1}^{j}\left(-1\right)^{k-1}\binom{\theta\left(x\right)}{k}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-403bb71a9034acea669385c5d53131e3_l3.png)
c’est-à-dire :
![Rendered by QuickLaTeX.com \[a_{j}=\sum_{x\in X}\left[\sum_{k=0}^{j}\left(-1\right)^{k}\binom{\theta\left(x\right)}{k}\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fdfb498a7a5753826e7c28e14f95a585_l3.png)
Enfin, d’après le lemme 1 et son corollaire, chacune des sommes internes est du signe de
5 – Une jolie application d’une inégalité de Bonferroni
Les 30-èmes OIM (Olympiades Internationales de Mathématiques) se sont tenues en Allemagne en 1989. Le 6-ème problème proposé était le suivant :
Une permutation ![]() de l’ensemble
de l’ensemble ![]() , où
, où ![]() , possède la propriété
, possède la propriété ![]() s’il existe au moins un indice
s’il existe au moins un indice ![]() tel que
tel que ![]()
Prouver que, pour tout ![]() le nombre de permutations possédant la propriété
le nombre de permutations possédant la propriété ![]() est supérieur au nombre de celles qui ne la possèdent pas.
est supérieur au nombre de celles qui ne la possèdent pas.
Dans ce contexte, si ![]() , on appelle « permutation de l’ensemble
, on appelle « permutation de l’ensemble ![]() » toute liste de longueur
» toute liste de longueur ![]() constituée exactement des entiers de
constituée exactement des entiers de ![]() à
à ![]() mais dans un ordre quelconque. Il est bien connu qu’il existe
mais dans un ordre quelconque. Il est bien connu qu’il existe ![]() telles permutations.
telles permutations.
Cela dit, notons ![]() l’ensemble des permutations de l’ensemble
l’ensemble des permutations de l’ensemble ![]() , pour lesquelles
, pour lesquelles ![]() et
et ![]() occupent des positions contigües (avec
occupent des positions contigües (avec ![]() ).
).
Par exemple, pour ![]() , les permutations
, les permutations ![]() et
et ![]() appartiennent à
appartiennent à ![]() puisque
puisque ![]() et
et ![]() se retrouvent côte à côte; alors que la permutation
se retrouvent côte à côte; alors que la permutation ![]() n’appartient pas à
n’appartient pas à ![]() .
.
Mais revenons au cas général…
Le nombre de permutations de ![]() possédant la propriété
possédant la propriété ![]() est :
est :
![Rendered by QuickLaTeX.com \[\varphi_{n}=\#\bigcup_{i=1}^{n}A_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9ca15ec57834c97eec6ada595aba5373_l3.png)
![Rendered by QuickLaTeX.com \[\varphi_{n}\geqslant\sum_{i=1}^{n}\#A_{i}-\sum_{1\leqslant i<j\leqslant n}\#\left(A_{i}\cap A_{j}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f0db1410a1c9bc00e03e1905809f4df1_l3.png)
![]()
![]()
![]()
Quant au nombre de permutations ne possédant pas la propriété P, il vaut :
![]()
Or, manifestement :
![]()
Et voilà !
Vos questions ou remarques seront toujours les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

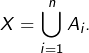 Pour tout
Pour tout