
1 – De quoi s’agit-il ?
Que se cache-t-il derrière les mots condition nécessaire et condition suffisante ?
Imaginons la situation suivante …
Vous effectuez des démarches administratives et vous avez besoin d’un document particulier (un acte de naissance, par exemple).
Pour que ce document puisse vous être délivré, on vous demande de vous présenter à la mairie, muni(e) d’une attestation de domicile et d’une pièce d’identité.
Si vous fournissez seulement l’attestation de domicile mais aucune pièce d’identité, l’officier d’état civil refusera de vous remettre le document demandé.
Essayons de formaliser un peu cette histoire et considérons les deux phrases (on dit aussi, deux propositions) :
- Phrase 1 : je me présente à la mairie muni(e) d’une attestation de domicile.
- Phrase 2 : j’obtiens, de la part de l’officier d’état civil, le document dont j’ai besoin.
On comprend que la phrase 1 exprime une condition qui doit être remplie pour que la phrase 2 soit vraie, mais que cette condition ne suffit pas à elle seule.
La condition exprimée par la phrase 1 est nécessaire (à l’obtention du document), mais elle n’est pas suffisante.
Si la phrase 1 est remplacée par « je me présente à la mairie muni(e) d’une attestation de domicile et d’une pièce d’identité », on obtient une condition nécessaire et suffisante.
Et si cette phrase est remplacée par « je me présente à la mairie muni(e) d’un magnifique bouquet de fleurs », on obtient une condition qui n’est sans doute ni nécessaire ni suffisante …

En mathématiques, on cherche en permanence à déterminer la nature du lien logique qui peut exister entre deux (ou plusieurs) propositions.
Parfois, une condition du type « la proposition ![]() est vraie » s’avèrera nécessaire mais non suffisante pour qu’une proposition
est vraie » s’avèrera nécessaire mais non suffisante pour qu’une proposition ![]() soit vraie; parfois elle sera suffisante mais non nécessaire.
soit vraie; parfois elle sera suffisante mais non nécessaire.
Il arrivera aussi que ![]() soit nécessaire et suffisante à la réalisation de
soit nécessaire et suffisante à la réalisation de ![]() On dit dans ce cas que les propositions
On dit dans ce cas que les propositions ![]() et
et ![]() sont équivalentes.
sont équivalentes.
Passons maintenant à l’étude d’exemples mathématiques …
2 – deux, quatre, huit
Considérons, pour tout entier naturel n, les trois propositions suivantes :
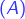 :
:  est multiple de 2
est multiple de 2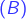 :
:  est multiple de 4
est multiple de 4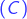 :
:  est multiple de 8
est multiple de 8
Il est immédiat que ![]() et que
et que ![]() .
.
En effet, si ![]() est vérifiée, alors il existe un entier naturel
est vérifiée, alors il existe un entier naturel ![]() tel que
tel que ![]() , ce qu’on peut aussi écrire
, ce qu’on peut aussi écrire ![]() , avec
, avec ![]() . Ceci prouve que
. Ceci prouve que ![]() est vérifiée.
est vérifiée.
L’argument est similaire pour la seconde implication.
On voit donc que ![]() est une condition suffisante pour
est une condition suffisante pour ![]() et que
et que ![]() est une condition nécessaire pour
est une condition nécessaire pour ![]() .
.
Mais ![]() n’est pas une condition nécessaire pour
n’est pas une condition nécessaire pour ![]() : un entier
: un entier ![]() multiple de 4 n’a aucune raison d’être multiple de 8 (par exemple :
multiple de 4 n’a aucune raison d’être multiple de 8 (par exemple : ![]() ).
).
Et de même ![]() n’est pas une condition suffisante pour
n’est pas une condition suffisante pour ![]() : un entier
: un entier ![]() multiple de 2 n’a aucune raison d’être multiple de 4 (par exemple :
multiple de 2 n’a aucune raison d’être multiple de 4 (par exemple : ![]() ).
).
On peut alors se demander quelle pourrait être une CNS (acronyme de « Condition Nécessaire et Suffisante ») pour ![]() soit vraie, autrement dit : quel pourrait être un critère de divisibilité par 4 ?
soit vraie, autrement dit : quel pourrait être un critère de divisibilité par 4 ?
Une possibilité est la suivante (on note ![]() le chiffre des unités de
le chiffre des unités de ![]() et
et ![]() son chiffre des dizaines) :
son chiffre des dizaines) :
![]() : l’entier formé par
: l’entier formé par ![]() et
et ![]() (dans cet ordre, à savoir l’entier
(dans cet ordre, à savoir l’entier ![]() ) est multiple de 4.
) est multiple de 4.
Dans l’équivalence entre ![]() et
et ![]() , le sens « utile » est certainement
, le sens « utile » est certainement ![]() . Par exemple, l’entier 12131487624 est certainement multiple de 4 puisque c’est le cas de 24 .
. Par exemple, l’entier 12131487624 est certainement multiple de 4 puisque c’est le cas de 24 .
Bien sûr, il faut expliquer pourquoi cette condition ![]() est équivalente à
est équivalente à ![]() . Vous pouvez probablement produire vous-même une preuve de cette équivalence. Et si nécessaire, un simple clic vous donnera accès à tous les détails …
. Vous pouvez probablement produire vous-même une preuve de cette équivalence. Et si nécessaire, un simple clic vous donnera accès à tous les détails …
Preuve (cliquer pour déplier / replier)
On va avoir besoin d’effectuer la division de ![]() par 100 en écrivant :
par 100 en écrivant :
![]()
![]()
Il s’agit donc de prouver que si ![]() est multiple de 4, alors
est multiple de 4, alors ![]() est multiple de 4 puis d’établir l’implication réciproque.
est multiple de 4 puis d’établir l’implication réciproque.
- La condition
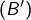 est nécessaire : en effet, si
est nécessaire : en effet, si 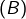 est vraie, alors il existe un entier naturel
est vraie, alors il existe un entier naturel 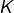 tel que
tel que
c’est-à-dire![Rendered by QuickLaTeX.com \[n=4K\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-09a54868e611dcc722beec8fdd740325_l3.png)
ou encore![Rendered by QuickLaTeX.com \[r=4K-100q\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0cd9fb0391abf0155868da4217e7a3f3_l3.png)
ce qui prouve que![Rendered by QuickLaTeX.com \[r=4\left(K-25q\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fd6650b47b1ab476e3f7ab157683d8be_l3.png)
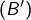 est vraie.
est vraie. - La condition
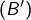 est suffisante : en effet; si
est suffisante : en effet; si  est multiple de 4, alors (vu que 100 est multiple de 4), on constate que
est multiple de 4, alors (vu que 100 est multiple de 4), on constate que 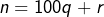 est aussi multiple de 4.
est aussi multiple de 4.
L’équivalence des propositions ![]() et
et ![]() est un exemple parmi les plus simples de critère de divisibilité. Pour en savoir plus à ce sujet, on pourra consulter cet article.
est un exemple parmi les plus simples de critère de divisibilité. Pour en savoir plus à ce sujet, on pourra consulter cet article.
3 – N est pair vs. le carré de N est pair
Rappelons qu’un nombre entier est dit pair lorsqu’il est le double d’un entier (autrement dit, lorsqu’il est multiple de 2).
Plus formellement : l’entier ![]() est pair lorsqu’il existe un entier
est pair lorsqu’il existe un entier ![]() tel que
tel que ![]() .
.
Les entiers pairs sont :
![]()
Il en existe évidemment une infinité !
Considérons un entier ![]() , positif ou nul, ainsi que les deux propositions :
, positif ou nul, ainsi que les deux propositions :
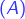 :
:  est pair
est pair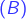 :
: 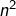 est pair
est pair
Il est facile de voir que ![]() est une conséquence de
est une conséquence de ![]() . En effet, l’hypothèse
. En effet, l’hypothèse ![]() se traduit par l’existence d’un entier naturel
se traduit par l’existence d’un entier naturel ![]() tel que
tel que ![]() . On en déduit que :
. On en déduit que :
![]()
Nous venons de prouver que ![]() implique
implique ![]() , autrement dit que
, autrement dit que ![]() est une conséquence de
est une conséquence de ![]() . Ceci se note conventionnellement :
. Ceci se note conventionnellement :
![]()
Il revient au même de dire que ![]() est une condition suffisante pour que
est une condition suffisante pour que ![]() soit réalisée. Ce vocabulaire est très clair : il suffit que la proposition
soit réalisée. Ce vocabulaire est très clair : il suffit que la proposition ![]() soit vraie pour que
soit vraie pour que ![]() soit aussi vraie.
soit aussi vraie.
Autre façon de dire la même chose : ![]() est une condition nécessaire pour que
est une condition nécessaire pour que ![]() soit réalisée. Là encore, la terminologie est limpide : si
soit réalisée. Là encore, la terminologie est limpide : si ![]() est vraie, alors
est vraie, alors ![]() est nécessairement vraie.
est nécessairement vraie.
Revenons maintenant à notre exemple.
Est-ce que, réciproquement, ![]() serait une condition suffisante pour que
serait une condition suffisante pour que ![]() soit réalisée ?
soit réalisée ?
La réponse est oui. Supposons en effet que ![]() soit pair et prouvons que
soit pair et prouvons que ![]() est pair.
est pair.
Imaginons un instant que ce ne soit pas le cas, autrement dit que ![]() soit impair. On pourrait donc écrire
soit impair. On pourrait donc écrire ![]() sous la forme
sous la forme ![]() (un entier impair est en effet le successeur d’un entier pair). Il en résulterait que :
(un entier impair est en effet le successeur d’un entier pair). Il en résulterait que :
![]()
Au final, nous avons prouvé que chacune des deux propositions ![]() et
et ![]() est conséquence de l’autre, ce qu’on exprime en disant qu’elles sont équivalentes. Et ceci se note :
est conséquence de l’autre, ce qu’on exprime en disant qu’elles sont équivalentes. Et ceci se note :
![]()
Si cet article vous a permis d’y voir plus clair, dites-le moi en laissant un commentaire ci-dessous ou bien en passant par le formulaire de contact ! Ca me fera plaisir 🙂

Merci beaucoup, des exemples simples et concis qui permettent de mieux s’y retrouver 🙂