Deux théorèmes sur les polynômes

On se propose d’établir, par des moyens élémentaires, deux résultats sur les polynômes, qui sont à la fois fondamentaux et d’un usage permanent en calcul algébrique.

Cet article s’adresse principalement à des élèves de terminale qui se destinent à des études supérieures scientifiques. La connaissance du principe de récurrence ainsi qu’un minimum d’habitude de la notation $\Sigma$ sont requis.

Commençons par rappeler une …

Définition

On dit de $f:\mathbb{R}\rightarrow\mathbb{R}$ que c’est une fonction polynôme lorsqu’il existe un entier naturel $n$ et des réels $a_{0},\cdots,a_{n}$ tels que :

$\forall x\in\mathbb{R},\thinspace f\left(x\right)=\sum_{k=0}^{n}a_{k}x^{k}$

Voici maintenant les deux théorèmes que nous avons en ligne de mire…

Théorème A

Soit $P$ une fonction polynôme et soit $\alpha\in\mathbb{R}$ tel que $P\left(\alpha\right)=0$ . Il existe alors une fonction polynôme $Q$ telle que :

$\forall x\in\mathbb{R},\thinspace P\left(x\right)=\left(x-\alpha\right)Q\left(x\right)$

Théorème B

Soit $n$ un entier naturel et soient des réels $a_{0},\cdots,a_{n}$ et $b_{0},\cdots,b_{n}$ tels que :

$\forall x\in\mathbb{R},\thinspace\sum_{k=0}^{n}a_{k}x^{k}=\sum_{k=0}^{n}b_{k}x^{k}$

Alors :

$\forall k\in\llbracket0,n\rrbracket,\thinspace a_{k}=b_{k}$

En pratique, lorsqu’on passe de

$\forall x\in\mathbb{R},\thinspace\sum_{k=0}^{n}a_{k}x^{k}=\sum_{k=0}^{n}b_{k}x^{k}$

$\forall k\in\llbracket0,n\rrbracket,\thinspace a_{k}=b_{k}$

on dit qu’on procède par “ identification des coefficients ”.

Le théorème B pourrait donc s’appeler le “ théorème d’identification polynomiale ”. Mais c’est une appellation non officielle : à un niveau plus avancé, on dira plutôt que le théorème B exprime, pour tout $n\in\mathbb{N}$ , l’indépendance linéaire de la famille de monômes $\left(x\mapsto x^{k}\right)_{0\leqslant k\leqslant n}$ .

Si vous êtes pressé(e) de voir comment s’utilisent concrètement ces deux théorèmes, vous pouvez directement passer à la section 5 … Mais l’objet principal de cet article se concentre aux sections 1 à 3, où les théorèmes en question sont établis.

1 – Une identité remarquable

Nous allons prouver qu’étant donnés un entier $n\geqslant2$ et deux réels $a,b$ quelconques :

$\fcolorbox{black}{myBlue}{$\displaystyle{a^{n}-b^{n}=\left(a-b\right)\sum_{k=1}^{n}a^{n-k}b^{k-1}}$}$

Procédons par récurrence et considérons l’assertion

$\left(\mathcal{A}_{n}\right)\::\qquad\forall\left(a,b\right)\in\mathbb{R}^{2},\:a^{n}-b^{n}=\left(a-b\right)\sum_{k=1}^{n}a^{n-k}b^{k-1}$

$\left(\mathcal{A}_{2}\right)$ est bien connue dès la fin du collège ! Il s’agit de l’identité remarquable :

$\boxed{\forall\left(a,b\right)\in\mathbb{R}^{2},\:a^{2}-b^{2}=\left(a-b\right)\left(a+b\right)}$

Ceci initialise notre récurrence. Passons à l’hérédité, en supposant $\left(\mathcal{A}_{n}\right)$ vraie pour un certain $n\geqslant2$ (c’est l’hypothèse de récurrence). Soient alors $a,b$ deux réels quelconques.

On observe que :

$a^{n+1}-b^{n+1}=b^{n}\left(a-b\right)+a\left(a^{n}-b^{n}\right)$

d’où, d’après l’hypothèse de récurrence :

$a^{n+1}-b^{n+1}=b^{n}\left(a-b\right)+a\left(a-b\right)\sum_{k=1}^{n}a^{n-k}b^{k-1}$

On peut maintenant factoriser par $\left(a-b\right)$ :

$\begin{matrix}a^{n+1}-b^{n+1} & = & {\displaystyle \left(a-b\right)\left[b^{n}+a\sum_{k=1}^{n}a^{n-k}b^{k-1}\right]}\\&&\\& = & {\displaystyle \left(a-b\right)\left[b^{n}+\sum_{k=1}^{n}a^{n+1-k}b^{k-1}\right]}\\&&\\& = & {\displaystyle \left(a-b\right)\sum_{k=1}^{n+1}a^{n+1-k}b^{k-1}}\end{matrix}$

comme souhaité.

Pour vous rafraîchir la mémoire au sujet des identités remarquables exigibles au lycée et de leurs principales applications, vous pouvez consulter la vidéo Identités Remarquables.

2 – Preuve du théorème A

Soit $P$ une fonction polynôme. Par définition, il existe $n\in\mathbb{N}$ et des réels $a_{0},\cdots,a_{n}$ tels que :

$\forall x\in\mathbb{R},\thinspace P\left(x\right)=\sum_{k=0}^{n}a_{k}x^{k}$

Soit $\alpha$ un réel vérifiant $P\left(\alpha\right)=0$ (on dit que $\alpha$ est une racine réelle de $P$ ).

Si $n=0,$ alors $P$ est une fonction constante, qui est fatalement la fonction nulle, ce qui rend triviale la propriété à démontrer (il suffit de prendre pour $Q$ la fonction nulle !).

Supposons désormais $n\geqslant1.$ On peut écrire, pour tout $x\in\mathbb{R}$ :

$P\left(x\right)=P\left(x\right)-P\left(\alpha\right)=\sum_{k=0}^{n}a_{k}\left(x^{k}-\alpha^{k}\right)=\sum_{k=1}^{n}a_{k}\left(x^{k}-\alpha^{k}\right)$

En appliquant l’identité remarquable établie à la première section, on voit que :

$P\left(x\right)=\sum_{k=1}^{n}a_{k}\left(x-\alpha\right)Q_{k}\left(x\right)$

où l’on a posé, pour tout $k\in\llbracket1,n\rrbracket$ :

$Q_{k}\left(x\right)=\sum_{j=1}^{k}x^{k-j}\alpha^{j-1}$

En définitive, on a bien montré que, pour tout $x\in\mathbb{R}$ :

$P\left(x\right)=\left(x-\alpha\right)Q\left(x\right)$

à condition de poser :

$Q\left(x\right)=\sum_{k=1}^{n}a_{k}\left(\sum_{j=1}^{k}x^{k-j}\alpha^{j-1}\right)$

De toute évidence, la fonction $Q$ ainsi définie est polynomiale, ce qui achève la preuve.

3 – Preuve du théorème B

Il s’agit de prouver que l’assertion :

$\left(\mathcal{P}_{n}\right)\::\qquad\begin{matrix}\forall\left(a_{0},\cdots,a_{n}\right)\in\mathbb{R}^{n+1},\thinspace\forall\left(b_{0},\cdots,b_{n}\right)\in\mathbb{R}^{n+1},\\\left({\displaystyle \forall x\in\mathbb{R},\thinspace\sum_{k=0}^{n}a_{k}x^{k}=\sum_{k=0}^{n}b_{k}x^{k}}\right)\Rightarrow\left(\forall k\in\llbracket0,n\rrbracket,\thinspace a_{k}=b_{k}\right)\end{matrix}$

est vraie pour tout $n\in\mathbb{N}.$

Par différence, il revient au même de prouver que l’assertion :

$\boxed{\left(\mathcal{Q}_{n}\right)\::\qquad\begin{matrix}\forall\left(c_{0},\cdots,c_{n}\right)\in\mathbb{R}^{n+1},\\\left({\displaystyle \forall x\in\mathbb{R},\thinspace\sum_{k=0}^{n}c_{k}x^{k}=0}\right)\Rightarrow\left(\forall k\in\llbracket0,n\rrbracket,\thinspace c_{k}=0\right)\end{matrix}}$

est vraie pour tout $n\in\mathbb{N},$ ce que nous allons faire par récurrence.

$\left(\mathcal{Q}_{0}\right)$ est vraie d’évidence (si $c_{0}$ est nul, alors $c_{0}$ est nul… rien de très exaltant !).

Supposons $\left(\mathcal{Q}_{n}\right)$ vraie pour un certain $n\in\mathbb{N}$ et soient alors $c_{0},\cdots,c_{n+1}$ des réels tels que :

( $\star$ ) $\forall x\in\mathbb{R},\thinspace\sum_{k=0}^{n+1}c_{k}x^{k}=0$

En choisissant $x=0,$ il vient $c_{0}=0.$

Par ailleurs, en dérivant chaque membre de $\left(\star\right),$ on obtient :

$\forall x\in\mathbb{R},\thinspace\sum_{k=1}^{n+1}kc_{k}x^{k-1}=0$

c’est-à-dire, après ré-indexation :

$\forall x\in\mathbb{R},\thinspace\sum_{k=0}^{n}\left(k+1\right)c_{k+1}x^{k}=0$

Il s’ensuit, d’après $\left(\mathcal{Q}_{n}\right),$ que $c_{1}=\cdots=c_{n+1}=0.$

Bref, les coefficients $c_{0},\cdots,c_{n+1}$ sont tous nuls. CQFD.

4 – Degré d’un polynôme non nul

Soit $P$ une fonction polynôme, qui n’est pas la fonction nulle.
Il existe $n\in\mathbb{N}$ et des réels $a_{0},\cdots,a_{n}$ tels que :

$\forall x\in\mathbb{R},\thinspace P\left(x\right)=\sum_{k=0}^{n}a_{k}x^{k}$

et de plus, l’un au moins de coefficients $a_{k}$ est non nul.

On peut donc supposer, sans perte de généralité, que $a_{n}\neq0.$ Avec cette petite contrainte, l’entier $n$ est déterminé de manière unique.

En effet, s’il existait deux entiers $m,n$ et des coefficients $a_{0},\cdots,a_{m}$ ainsi que $b_{0},\cdots,b_{n}$ tels que :

$m\neq n,\qquad a_{m}\neq0,\qquad b_{n}\neq0\qquad\text{et}\qquad\forall x\in\mathbb{R},\thinspace\sum_{k=0}^{m}a_{k}x^{k}=\sum_{k=0}^{n}b_{k}x^{k}$

on serait aussitôt en contradiction avec le théorème B.

Cet entier, qui est donc bien déterminé, s’appelle le degré de $P$ et il est noté $\deg\left(P\right).$

Définition

$\deg\left(P\right)$ est le plus grand exposant présent dans l’expression développée de $P$

→ Par exemple, si l’on pose :

$\forall x\in\mathbb{R},\thinspace f\left(x\right)=x^{2}+4x^{4}-x^{3}+1$

alors $\deg\left(f\right)=4$ .

Il n’est pas difficile de montrer que si deux fonctions polynômes (non nulles) ont pour degrés respectifs $p$ et $q$ , alors leur produit a pour degré $p+q$ .

→ Par exemple, si l’on pose :

$\forall x\in\mathbb{R},\thinspace g\left(x\right)=\left(x^{2}+1\right)^{2}\left(x-2\right)$

alors $\deg\left(g\right)=5$ .

5 – Utilisation combinée des deux théorèmes

Considérons le polynôme P défini par :

$P\left(x\right)=x^{3}-5x^{2}+2x+8$

et cherchons à le factoriser.

Pour cela, commençons par chercher une racine “ évidente ”…

Après quelques tâtonnements (cf. remarque 1 en fin de section), on découvre que :

$P\left(2\right)=2^{3}-5\times2^{2}+2\times2+8=8-20+4+8=0$

Le théorème A nous permet d’affirmer qu’il existe un polynôme Q tel que :

( $\star$ ) $\forall x\in\mathbb{R},\thinspace P\left(x\right)=\left(x-2\right)Q\left(x\right)$

Comme $\deg\left(P\right)=3,$ alors (cf. section 4) $\deg\left(Q\right)=2.$

Il existe donc des réels $a,b,c$ (avec $a\neq0$ ) tels que $Q\left(x\right)=ax^{2}+bx+c,$ pour tout $x\in\mathbb{R}.$

La relation $(\star)$ précédente devient :

$\fcolorbox{black}{myBlue}{$\forall x\in\mathbb{R},\thinspace x^{3}-5x^{2}+2x+8=\left(x-2\right)\left(ax^{2}+bx+c\right)$}$

c’est-à-dire, en développant le second membre :

$\forall x\in\mathbb{R},\thinspace x^{3}-5x^{2}+2x+8=ax^{3}+\left(b-2a\right)x^{2}+\left(c-2b\right)x-2c$

C’est là qu’intervient le théorème B. En identifiant les coefficients, on parvient au système :

$\left\{ \begin{matrix}a & = & 1\\b-2a & = & -5\\c-2b & = & 2\\-2c & = & 8\end{matrix}\right.$

d’où l’on tire facilement :

$a=1\qquad b=-3\qquad c=-4$

On est ainsi parvenu à la formule :

$\fcolorbox{black}{myBlue}{$\forall x\in\mathbb{R},\thinspace x^{3}-5x^{2}+2x+8=\left(x-2\right)\left(x^{2}-3x-4\right)$}$

Tant qu’à faire, allons jusqu’au bout du processus de factorisation !

Le trinôme $x^{2}-3x-4$ ayant pour discriminant $\Delta=\left(-3\right)^{2}-4\times1\times\left(-4\right)=25,$ ses racines sont :

$x_{1}=\frac{3+5}{2}=4\qquad\text{et}\qquad x_{2}=\frac{3-5}{2}=-1$

On peut finalement conclure que :

$\fcolorbox{black}{myBlue}{$\forall x\in\mathbb{R},\:x^{3}-5x^{2}+2x+8=\left(x-2\right)\left(x-4\right)\left(x+1\right)$}$

Remarque 1

On peut éviter les tâtonnements en utilisant le “ test des racines rationnelles ”, qui est présenté dans l’article Comment factoriser un polynôme ?

Remarque 2

On pouvait accélérer un peu le calcul ci-dessus en donnant d’emblée les valeurs des coefficients $a$ et $c$ . D’une manière un peu plus générale, lorsqu’on détecte une racine $\alpha$ pour le polynôme $P,$ deux coefficients de $Q$ sont accessibles sans calcul : le coefficient de plus haut degré et le coefficient constant.

Remarque 3

La technique d’identification présentée ici demeure assez rudimentaire. Il est, en pratique, plus efficace de poser la division euclidienne de $P\left(x\right)$ par $x-\alpha$ , ou d’appliquer un schéma de Horner, mais ceci fera l’objet d’un autre article 🙂

Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.

Partager cet article

Cet article a 5 commentaires

Oncle_Junior 19 Oct 2022 Répondre

Il me semblait que Q1 avec cette formule donnait une somme allant de 1 à 1… ! Ah ben oui au temps pour moi 😊
Je m’étais mis en tête que cela donnait la somme sur l’ensemble vide donc 0, mais la somme se réduit à un terme. Je ne dois pas pratiquer assez et surtout j’ai omis de prendre feuille et stylo !

Merci à vous, bonne soirée 🙂
Oncle_Junior 19 Oct 2022 Répondre

Bonjour Monsieur,
Merci pour cet article 🙂
Il me semble qu’il faut poser Q1=1 et définir les Qk à partir de k=2 dans la section 2.
Bien à vous.
1. René Adad 19 Oct 2022 Répondre
  
  La formule proposée pour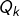 $Q_k$ , à savoir
  
  $Q_k=\sum_{j=1}^{k}x^{k-j}\alpha^{j-1}$
  
  donne en particulier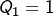 $Q_1=1$ , donc tout va bien 🙂
Oncle_Junior 19 Oct 2022 Répondre

Bonjour Monsieur,
Merci pour ces rappels 🙂

Pour les polynômes Qk de la section 2, il me semble qu’ils peuvent rester inchangés pour k entre 2 et n. En revanche, l’identité de la section précédente étant valide et démontrée à partir du rang 2, il me semble qu’il faudrait poser Q1(x)=x-a.

Bien à vous
1. René Adad 19 Oct 2022 Répondre
  
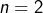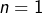  Je pense qu’il n’y a en fait aucun problème puisque, certes, la formule de factorisation établie à la section 1 l’a été à partir de $n=2$ , mais elle est néanmoins bien valide (et triviale !) pour $n=1$ .