Avant la réforme des programmes entrée en vigueur à la rentrée 2012, la technique d’intégration par parties était enseignée en terminale scientifique et l’on pouvait tomber sur des exercices relativement intéressants, où le calcul d’une intégrale était envisageable autrement qu’en connaissant d’emblée une primitive.
Après ladite réforme, cette technique de calcul ne figurait plus au programme. Les concepteurs de sujets de bac, qui envisageaient une question de calcul intégral, n’avaient plus beaucoup de choix : privés de cet outil, ils étaient contraints de se limiter à la courte liste des fonctions pour lesquelles une primitive est censée être connue des élèves ou bien, à la rigueur, de faire « constater » aux candidats que telle fonction est une primitive de telle autre. Le sujet était devenu quasi-stérile…
Mais restons optimiste ! A la faveur des nouveaux programmes de 2019, cette technique fondamentale va probablement retrouver la place qu’elle occupait autrefois (et qui, selon moi, lui revient), tout au moins pour les élèves ayant fait le choix d’un enseignement renforcé en mathématiques.
Section 1
Le point de départ est la formule de dérivation d’un produit…
On sait que si ![Rendered by QuickLaTeX.com u,v:[a,b]\rightarrow\mathbb{R}](https://math-os.com/wp-content/ql-cache/quicklatex.com-256f2d7ff63de0bbe907f752aae039ef_l3.png) sont deux fonctions dérivables, alors :
sont deux fonctions dérivables, alors :
![Rendered by QuickLaTeX.com \[\left(uv\right)'=u'v+uv'\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-63d003ee7c05cb019384b27258239056_l3.png)
Faisons maintenant une hypothèse plus forte, à savoir que 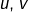 soient de classe
soient de classe 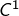 (c’est-à-dire dérivables et à dérivée continue). On peut alors intégrer l’égalité ci-dessus sur
(c’est-à-dire dérivables et à dérivée continue). On peut alors intégrer l’égalité ci-dessus sur ![Rendered by QuickLaTeX.com [a,b]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3931b6562a161a1275d216a8ceeb04fa_l3.png) pour obtenir :
pour obtenir :
![Rendered by QuickLaTeX.com \[\int_{a}^{b}\left(uv\right)'\left(t\right)\thinspace dt=\int_{a}^{b}u'\left(t\right)\thinspace v\left(t\right)\thinspace dt+\int_{a}^{b}u\left(t\right)\thinspace v'\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bc53d344f48861484c0e3f1d19fe6643_l3.png)
c’est-à-dire :
C’est la formule d’intégration par parties (IPP).
Deux intégrales figurent dans cette formule. Donc, si l’on sait calculer l’une d’elles, alors on sait aussi calculer l’autre ! C’est aussi simple que ça.
2 – Un premier exemple
Commençons avec l’intégrale :
![Rendered by QuickLaTeX.com \[A=\int_{0}^{1}\thinspace t\thinspace e^{-t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1348e8daf0f1a7bcd086e0a76c4a6849_l3.png)
Toute l’astuce consiste à choisir un « bon » couple 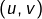 , autrement dit : voir la fonction
, autrement dit : voir la fonction 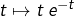 comme le produit de deux fonctions… l’une qu’on va dériver (et qu’on notera
comme le produit de deux fonctions… l’une qu’on va dériver (et qu’on notera  ) et l’autre qu’on va primitiver (et qu’on notera
) et l’autre qu’on va primitiver (et qu’on notera 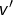 ).
).
Le plus naturel consiste à poser :
![Rendered by QuickLaTeX.com \[u(t)=t\qquad\text{et}\qquad v'(t)=e^{-t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b5b19e3625ef3c2504c3a8aa809a6c1b_l3.png)
puis :
![Rendered by QuickLaTeX.com \[u'\left(t\right)=1\qquad\text{et}\qquad v\left(t\right)=-e^{-t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-870dd668aeffe46037e7809ccf5ce335_l3.png)
Noter que pour 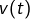 , on a choisi
, on a choisi  comme primitive de
comme primitive de 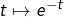 . On aurait pu, tout aussi bien, choisir
. On aurait pu, tout aussi bien, choisir 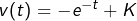 , avec une valeur arbitraire pour la constante
, avec une valeur arbitraire pour la constante 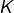 (la suite du calcul n’en serait pas affectée). Le plus simple consiste à choisir
(la suite du calcul n’en serait pas affectée). Le plus simple consiste à choisir 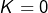 .
.
En appliquant alors la formule d’IPP, on obtient :
![Rendered by QuickLaTeX.com \[A=-\frac{1}{e}+\int_{0}^{1}e^{-t}\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c44abaa9faecfe35c17eaeb1bfb0d91f_l3.png)
soit finalement :
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{1}\thinspace t\thinspace e^{-t}\thinspace dt=1-\frac{2}{e}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b6220ba62630370350b7d147430a9dd6_l3.png)
3 – La notation « crochets »
Il est d’usage courant, si 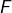 désigne une fonction définie sur
désigne une fonction définie sur ![Rendered by QuickLaTeX.com [a,b]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3931b6562a161a1275d216a8ceeb04fa_l3.png) , de noter
, de noter ![Rendered by QuickLaTeX.com [F(t)]_{a}^{b}](https://math-os.com/wp-content/ql-cache/quicklatex.com-e1cdba32872e00780d00921d65383deb_l3.png) pour désigner la différence
pour désigner la différence 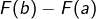 , qu’on appelle parfois la variation de
, qu’on appelle parfois la variation de 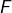 entre
entre  et
et 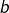 .
.
Si ![Rendered by QuickLaTeX.com f:[a,b]\rightarrow\mathbb{R}](https://math-os.com/wp-content/ql-cache/quicklatex.com-c6b6b8a0e43a2c074bc4fa6e9d8bddab_l3.png) est continue et si
est continue et si 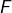 désigne une primitive de
désigne une primitive de  , l’égalité
, l’égalité
![Rendered by QuickLaTeX.com \[\int_{a}^{b}f\left(t\right)\thinspace dt=F\left(b\right)-F\left(a\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6febd201f7fe3f8a7bdc503ab481e858_l3.png)
peut donc s’écrire
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\int_{a}^{b}f\left(t\right)\thinspace dt=\left[F\left(t\right)\right]_{a}^{b}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ea933565e32d162eb3a640f941f3e16a_l3.png)
ou éventuellement
![Rendered by QuickLaTeX.com \[\int_{a}^{b}f\left(t\right)\thinspace dt=\left[F\left(t\right)\right]_{t=a}^{b}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-67514ac41e8d801addac5640bd8acc46_l3.png)
cette dernière notation pouvant s’avérer utile dans certains contextes, où d’autres symboles sont présents en plus de celui représentant la variable d’intégration. Par exemple, si
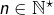
et
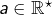
:
![Rendered by QuickLaTeX.com \[\int_0^xt^ne^{-at}\,dt=\left[-\frac{t^n}{a}e^{-at}\right]_{t=0}^x+\frac{n}{a}\int_0^xt^{n-1}e^{-at}\,dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-702a7eae255c02666fe9975b3d03a43e_l3.png)
L’intérêt d’écrire
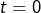
plutôt que
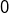
est clair : cela permet d’éviter, dans le calcul du terme entre crochets, de remplacer une
autre lettre que
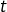
par
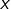
et par
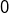
!
4 – Trois exemples supplémentaires
Calculons chacune des intégrales suivantes :
![Rendered by QuickLaTeX.com \[B=\int_{0}^{1}t^{2}\thinspace e^{-t}\thinspace dt\qquad C=\int_{0}^{\pi}\sin^{2}\left(t\right)\thinspace dt\qquad D=\int_{1}^{e^{2}}\ln\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9a9f43ffd15dd4e74ad009d18d707608_l3.png)
➡ Pour 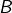 , nous allons intégrer par parties en posant :
, nous allons intégrer par parties en posant :
![Rendered by QuickLaTeX.com \[u\left(t\right)=t^{2}\qquad\text{et}\qquad v'\left(t\right)=e^{-t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4115334ba13e9f368653443cf61a5d53_l3.png)
ainsi que :
![Rendered by QuickLaTeX.com \[u'\left(t\right)=2t\qquad\text{et}\qquad v\left(t\right)=-e^{-t}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3e2993f85a0a5ee957b95901ca9cb783_l3.png)
ce qui conduit à :
![Rendered by QuickLaTeX.com \[B=\left[-t^{2}\thinspace e^{-t}\right]_{0}^{1}-\int_{0}^{1}-2t\thinspace e^{-t}\thinspace dt=-\frac{1}{e}+2A\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7233a617ce6e0b7eff20b55c2446fadf_l3.png)
où
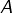
est l’intégrale calculée plus haut ! Ainsi :
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{1}t^{2}\thinspace e^{-t}\thinspace dt=2-\frac{5}{e}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa6d0a254c6d92735832d7d6bc91e267_l3.png)
➡ Pour 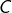 , nous allons intégrer par parties en posant :
, nous allons intégrer par parties en posant :
![Rendered by QuickLaTeX.com \[u\left(t\right)=\sin\left(t\right)\qquad\text{et}\qquad v'\left(t\right)=\sin\left(t\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e43babd40c11ae18736b8fd8138aee77_l3.png)
ainsi que :
![Rendered by QuickLaTeX.com \[u'\left(t\right)=\cos\left(t\right)\qquad\text{et}\qquad v\left(t\right)=-\cos\left(t\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-49e5592245cab61230edd183fd9014c1_l3.png)
ce qui donne :
![Rendered by QuickLaTeX.com \[C=\left[-\sin\left(t\right)\cos\left(t\right)\right]_{0}^{\pi}+\int_{0}^{\pi}\cos^{2}\left(t\right)\thinspace dt\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b29eabea6cde8c7d2ad288bb483db7d8_l3.png)
Le terme entre crochets est nul.
Quant à la dernière intégrale écrite, on a intérêt à l’écrire comme ceci :
![Rendered by QuickLaTeX.com \[\int_{0}^{\pi}\cos^{2}\left(t\right)\thinspace dt=\int_{0}^{\pi}\left(1-\sin^{2}\left(t\right)\right)\thinspace dt=\pi-C\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-03036f8bc63b14f20d3e114b2148e198_l3.png)
de sorte que
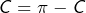
et finalement :
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{\pi}\sin^{2}\left(t\right)\thinspace dt=\frac{\pi}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3115454f4d80a25a096db7621e3c305e_l3.png)
Remarque
Intégrer par parties n’était pas un passage obligé pour le calcul de 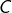 .
.
On pouvait linéariser l’expression 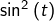 en écrivant que, pour tout
en écrivant que, pour tout ![Rendered by QuickLaTeX.com t\in\left[0,\pi\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2ddc4b54b410b686a13b0aa9c8463dcd_l3.png) :
:
![Rendered by QuickLaTeX.com \[\sin^{2}\left(t\right)=\frac{1-\cos\left(2t\right)}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9fcc4ac075894025476d49525edfab77_l3.png)
ce qui permet un calcul direct :
![Rendered by QuickLaTeX.com \[C=\left[\frac{t}{2}-\frac{\sin(2t)}{4}\right]_{0}^{\pi}=\frac{\pi}{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-342c6a59b1fd7b34eb42de2d977498af_l3.png)
➡ Enfin, pour 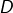 , il faut un petit peu d’astuce. Posons :
, il faut un petit peu d’astuce. Posons :
![Rendered by QuickLaTeX.com \[u\left(t\right)=\ln\left(t\right)\qquad\text{et}\qquad v'\left(t\right)=1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f7f2c228184a91de5882527087133ec7_l3.png)
ainsi que :
![Rendered by QuickLaTeX.com \[u'\left(t\right)=\frac{1}{t}\qquad\text{et}\qquad v\left(t\right)=t\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2f9c6965d1c6183e64b8023a70e7ca21_l3.png)
ce qui conduit à :
![Rendered by QuickLaTeX.com \[D=\left[t\ln\left(t\right)\right]_{1}^{e^{2}}-\int_{1}^{e^{2}}\thinspace dt=e^{2}\ln\left(e^{2}\right)-\left(e^{2}-1\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7d9a69b6ff346bd1a82cac2159063d64_l3.png)
soit finalement :
![Rendered by QuickLaTeX.com \[\boxed{\int_{1}^{e^{2}}\ln\left(t\right)\thinspace dt=e^{2}+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-17004e0b00507eaaa1a68cd950496ec6_l3.png)
Vos questions ou remarques sont les bienvenues. Vous pouvez laisser un commentaire ci-dessous ou bien passer par le formulaire de contact.
J’aime ça :
J’aime chargement…
![]()
![]() soient de classe
soient de classe ![]() (c’est-à-dire dérivables et à dérivée continue). On peut alors intégrer l’égalité ci-dessus sur
(c’est-à-dire dérivables et à dérivée continue). On peut alors intégrer l’égalité ci-dessus sur ![]() pour obtenir :
pour obtenir :![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{1}\thinspace t\thinspace e^{-t}\thinspace dt=1-\frac{2}{e}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b6220ba62630370350b7d147430a9dd6_l3.png)
![]() désigne une fonction définie sur
désigne une fonction définie sur ![]() , de noter
, de noter ![]() pour désigner la différence
pour désigner la différence ![]() , qu’on appelle parfois la variation de
, qu’on appelle parfois la variation de ![]() entre
entre ![]() et
et ![]() .
.![]() est continue et si
est continue et si ![]() désigne une primitive de
désigne une primitive de ![]() , l’égalité
, l’égalité![]()
![Rendered by QuickLaTeX.com \[\fcolorbox{black}{myBlue}{$\displaystyle{\int_{a}^{b}f\left(t\right)\thinspace dt=\left[F\left(t\right)\right]_{a}^{b}}$}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ea933565e32d162eb3a640f941f3e16a_l3.png)
![]()
![]()
![]()
![]() , nous allons intégrer par parties en posant :
, nous allons intégrer par parties en posant :![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{1}t^{2}\thinspace e^{-t}\thinspace dt=2-\frac{5}{e}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fa6d0a254c6d92735832d7d6bc91e267_l3.png)
![]() , nous allons intégrer par parties en posant :
, nous allons intégrer par parties en posant :![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\int_{0}^{\pi}\sin^{2}\left(t\right)\thinspace dt=\frac{\pi}{2}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3115454f4d80a25a096db7621e3c305e_l3.png)
![]() .
.![]() en écrivant que, pour tout
en écrivant que, pour tout ![]() :
:![]()
![]()
![]() , il faut un petit peu d’astuce. Posons :
, il faut un petit peu d’astuce. Posons :![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{\int_{1}^{e^{2}}\ln\left(t\right)\thinspace dt=e^{2}+1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-17004e0b00507eaaa1a68cd950496ec6_l3.png)

