Solutions détaillées de neuf exercices sur la notion de produit scalaire (fiche 02).
Cliquer ici pour accéder aux énoncés.


On sait que pour toute partie ![]() de
de ![]() :
:
![]()
![]()
![]()
![]()

Si ![]() et
et ![]() commutent, alors :
commutent, alors :
![]()
![]()
En conclusion : ![]() est symétrique si, et seulement si,
est symétrique si, et seulement si, ![]() et
et ![]() commutent.
commutent.

Fixons une BON ![]() de
de ![]() Pour toute forme linéaire
Pour toute forme linéaire ![]() sur
sur ![]() et pour tout
et pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[\varphi\left(x\right)=\varphi\left(\sum_{i=1}^{n}\left(x\mid e_{i}\right)e_{i}\right)=\sum_{i=1}^{n}\left(x\mid e_{i}\right)\thinspace\varphi\left(e_{i}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-adac21eafd455febc75a87050c2612ef_l3.png)
![Rendered by QuickLaTeX.com \[a=\sum_{i=1}^{n}\varphi\left(e_{i}\right)e_{i}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3423f05636282ac78d1c147c32f209d9_l3.png)
![Rendered by QuickLaTeX.com \[\varphi\left(x\right)=\sum_{i=1}^{n}\left(x\mid e_{i}\right)\left(a\mid e_{i}\right)=\left(a\mid x\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1246fc61cfd940996a03984d29b6138a_l3.png)
Remarque
Cette preuve fait explicitement intervenir une base de ![]() A comparer avec la preuve habituelle, rappelée dans l’énoncé, qui ne fait référence à aucune base particulière (ce qu’on exprime en disant que l’isomorphisme
A comparer avec la preuve habituelle, rappelée dans l’énoncé, qui ne fait référence à aucune base particulière (ce qu’on exprime en disant que l’isomorphisme ![]() est canonique).
est canonique).

L’application :
![]()
![]()
Notons ![]() le
le ![]() ème polynôme de Tchebytchev de 1ère espèce. Pour tout
ème polynôme de Tchebytchev de 1ère espèce. Pour tout ![]() :
:
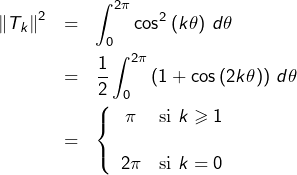
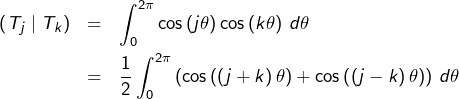
![Rendered by QuickLaTeX.com \[\left(T_{j}\mid T_{k}\right)=\frac{1}{2}\left[\frac{\sin\left(\left(j+k\right)\theta\right)}{j+k}+\frac{\sin\left(\left(j-k\right)\theta\right)}{j-k}\right]_{\theta=0}^{2\pi}=0 \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6b83d8af118651539b2c1c9472c2a988_l3.png)
Finalement la famille ![]() définie par :
définie par :
![]()

Soit ![]() conservant l’orthogonalité. Etant donnés
conservant l’orthogonalité. Etant donnés ![]() tels que
tels que ![]() on constate que
on constate que ![]() d’où
d’où ![]() c’est-à-dire
c’est-à-dire ![]()
Il existe donc ![]() tel que
tel que ![]() pour tout vecteur unitaire
pour tout vecteur unitaire ![]() et donc, pour tout
et donc, pour tout ![]() :
: ![]() Si
Si ![]() alors
alors ![]() et sinon, l’endomorphisme
et sinon, l’endomorphisme ![]()
conserve la norme, donc est un automorphisme orthogonal.
Bref, si ![]() converve l’orthogonalité, alors il existe
converve l’orthogonalité, alors il existe ![]() et
et ![]() tel que
tel que ![]()
Réciproquement, il est évident que tout endomorphisme de cette forme convient.
Remarque
La composée d’une homothétie non nulle par un automorphisme orthogonal est appelée une similitude. On distingue les similitudes directes (de déterminant ![]() des similitudes indirectes (de déterminant
des similitudes indirectes (de déterminant ![]()
L’application nulle est évidemment lipschitzienne.
Si ![]() et si
et si ![]() alors
alors ![]() en effet, pour tout
en effet, pour tout ![]() :
:
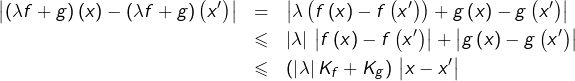
Notons ![]() le sous-espace de
le sous-espace de ![]() constitué des applications de classes
constitué des applications de classes ![]() Si l’on prouve que
Si l’on prouve que ![]() il en résultera que
il en résultera que ![]() car (inégalité des accroissements finis, combinée avec le fait que toute application continue sur un segment est bornée) :
car (inégalité des accroissements finis, combinée avec le fait que toute application continue sur un segment est bornée) : ![]() et donc
et donc ![]() Soit
Soit ![]() et soit
et soit ![]() la primitive de
la primitive de ![]() qui s’annule en
qui s’annule en ![]() On observe, en notant
On observe, en notant ![]() l’application constante
l’application constante ![]() que :
que :
![]()
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left(\Phi\mid f\right) & = & \left[\Phi\left(t\right)F\left(t\right)\right]_{0}^{1}-\int_{0}^{1}\varphi\left(t\right)F\left(t\right)\thinspace dt\\& = & -\left(\varphi\mid F\right)\\& = & 0\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-004d3378accaec80698089f6b912791e_l3.png)
En particulier :

Le fait que l’application
![]()
![]()
Avant de proposer un couple ![]() ne vérifiant pas cette relation, remarquons que si
ne vérifiant pas cette relation, remarquons que si ![]() sont telles que
sont telles que ![]() alors
alors ![]() et
et ![]() et donc :
et donc :
![Rendered by QuickLaTeX.com \begin{eqnarray*}N\left(f+g\right)^{2}+N\left(f-g\right)^{2} & = & \left(\int_{0}^{1}f\left(t\right)\thinspace dt+\int_{0}^{1}g\left(t\right)\thinspace dt\right)^{2}+\left(\int_{0}^{1}f\left(t\right)\thinspace dt-\int_{0}^{1}g\left(t\right)\thinspace dt\right)^{2}\\& = & 2\left[\left(\int_{0}^{1}f\left(t\right)\thinspace dt\right)^{2}+\left(\int_{0}^{1}g\left(t\right)\thinspace dt\right)^{2}\right]\\& = & 2\left[N\left(f\right)^{2}+N\left(g\right)^{2}\right]\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-6a2a270a2653b3a7e4fe9bd9f36a16b4_l3.png)
Cherchons donc un contre-exemple parmi les couples ![]() de fonctions continues positives telles qu’aucune des deux ne soit majorée par l’autre. Posons pour tout
de fonctions continues positives telles qu’aucune des deux ne soit majorée par l’autre. Posons pour tout ![]() :
:
![]()
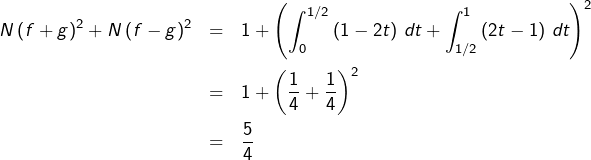
![]()

Notons ![]() Si
Si ![]() alors (d’après l’hypothèse de l’énoncé) :
alors (d’après l’hypothèse de l’énoncé) :
![Rendered by QuickLaTeX.com \[\left\Vert x\right\Vert ^{2}=\sum_{i=1}^{n}\left(x\mid e_{i}\right)^{2}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-34107014613eb520c69d07ff54fe9b60_l3.png)
Considérons un entier ![]() En remplaçant
En remplaçant ![]() par
par ![]() dans l’hypothèse, il vient :
dans l’hypothèse, il vient :
![Rendered by QuickLaTeX.com \[\left\Vert e_{j}\right\Vert ^{2}=\sum_{i=1}^{n}\left(e_{j}\mid e_{i}\right)^{2}\geqslant\left\Vert e_{j}\right\Vert ^{4}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-04ddb23bd838658074748a8a72577706_l3.png)
![Rendered by QuickLaTeX.com \[\left\Vert x\right\Vert ^{2}=\sum_{i=1}^{n}\left(x\mid e_{i}\right)^{2}=\left(x\mid e_{j}\right)^{2}\leqslant\left\Vert x\right\Vert ^{2}\left\Vert e_{j}\right\Vert ^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0da261435b65f8ecc9fe30c404b7e41c_l3.png)
Pour finir, en remplaçant ![]() par
par ![]() dans l’hypothèse, on voit que :
dans l’hypothèse, on voit que :
![Rendered by QuickLaTeX.com \[1=\left\Vert e_{j}\right\Vert ^{2}=\sum_{i=1}^{n}\left(e_{j}\mid e_{i}\right)^{2}=1+\sum_{{1\leqslant i\leqslant n\atop i\neq j}}\left(e_{j}\mid e_{i}\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b96c71c90aa5d3c13806d3ecdb412009_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{{1\leqslant i\leqslant n\atop i\neq j}}\left(e_{j}\mid e_{i}\right)^{2}=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5834dc2e1b26a13662c987405343ddc4_l3.png)

➣ L’endomorphisme ![]() ne possède pas d’adjoint :
ne possède pas d’adjoint :
Supposons l’existence de ![]() tel que :
tel que :
![]()
![]()
(![]() )
) ![]()
![]()
➣ Existence et calcul de l’adjoint de ![]() :
:
Pour tous ![]() :
:
![]()
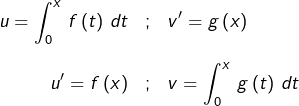
![Rendered by QuickLaTeX.com \begin{eqnarray*}\left(\psi\left(f\right)\mid g\right) & = & \left(\int_{0}^{1}\,f\left(t\right)\,dt\right)\left(\int_{0}^{1}\,g\left(t\right)\,dt\right)-\int_{0}^{1}\,f\left(x\right)\,\left(\int_{0}^{x}\,g\left(t\right)\,dt\right)\,dx\\& = & \int_{0}^{1}\,f\left(x\right)\left[\int_{0}^{1}\,g\left(t\right)\,dt-\int_{0}^{x}\,g\left(t\right)\,dt\right]\,dx\\& = & \int_{0}^{1}\,f\left(x\right)\,\int_{x}^{1}\,g\left(t\right)\,dt\end{eqnarray*}](https://math-os.com/wp-content/ql-cache/quicklatex.com-6921f084c7118d384e9358904c048263_l3.png)
![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
