Solutions détaillées de neuf exercices sur la notion de nombre premier (fiche 02).
Cliquer ici pour accéder aux énoncés.


Pour commencer :
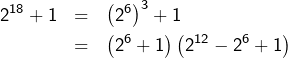
et de même :
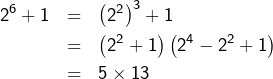
![]()
![]()
Soit ![]() et soit
et soit ![]() sa racine cubique entière.
sa racine cubique entière.
Supposons que ![]() ne possède aucun diviseur
ne possède aucun diviseur ![]() tel que
tel que ![]()
Montrons que ![]() est premier ou produit de deux nombres premiers, en écartant les autres possibilités :
est premier ou produit de deux nombres premiers, en écartant les autres possibilités :
- Déjà,
 ne peut pas posséder trois facteurs premiers distincts. En effet, si
ne peut pas posséder trois facteurs premiers distincts. En effet, si  sont premiers et divisent
sont premiers et divisent 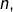 alors
alors 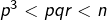 donc
donc 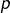 est un diviseur non trivial de
est un diviseur non trivial de 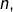 strictement inférieur à
strictement inférieur à 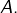
- Supposons maintenant que
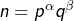 avec
avec 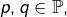
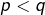 et
et 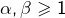 tels que
tels que 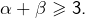 Si par exemple
Si par exemple 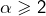 alors
alors 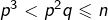 d’où
d’où 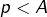 : contradiction. Même chose en supposant
: contradiction. Même chose en supposant 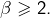 Donc
Donc 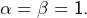
- On voit de même que
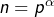 avec
avec 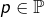 et
et 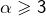 ne tient pas.
ne tient pas.
Les seules possibilités sont donc :
➣ ![]() avec
avec ![]() et
et ![]()
➣ ![]() avec
avec ![]() distincts.
distincts.
En conclusion, ![]() est un nombre premier ou bien le produit de deux nombres premiers.
est un nombre premier ou bien le produit de deux nombres premiers.
L’algorithme standard de primalité consiste à chercher d’éventuels diviseurs jusqu’à la racine carrée entière incluse. Il est expliqué en détail dans cet article ainsi que dans cette vidéo.
Sa transcription en Python est alors assez directe :
def ppfp(n):
if n < 2:
return None
elif n % 2 == 0:
return 2
d = 3
isprime = True
while (d * d <= n and isprime):
if n % d == 0:
isprime = False
else:
d += 2
if isprime:
return n
else:
return dA partir de là, il est facile de dresser la liste des facteurs premiers d’un entier ![]() Il suffit d’initialiser une variable à
Il suffit d’initialiser une variable à ![]() de le diviser par son PPFP et de recommencer … jusqu’à ce qu’on atteigne 1.
de le diviser par son PPFP et de recommencer … jusqu’à ce qu’on atteigne 1.
C’est ce que fait la fonction dfp (pour Décomposition en Facteurs Premiers) ci-dessous. La liste renvoyée contient la liste des facteurs premiers de ![]() (avec d’éventuelles répétitions bien entendu).
(avec d’éventuelles répétitions bien entendu).
def dfp(n):
L = []
x = n
while x > 1:
p = ppfp(x)
L.append(p)
x = x // p
return LExemple :
>>> dfp (1571427)
[3, 3, 3, 11, 11, 13, 37]Ce n’était pas demandé, mais on peut obtenir à partir de là une décomposition en facteurs premiers « compacte », c’est-à-dire une liste de couples (facteur premier, exposant). L’implémentation ci-dessous repose sur l’utilisation d’un dictionnaire :
dfpc(n):
L = dfp(n)
L.reverse()
couples = {}
while L != []:
q = L.pop()
if q in couples:
couples[q] = couples[q] + 1
else:
couples[q] = 1
return couplesExemple :
>>> dfpc (1571427)
{3: 3, 11: 2, 13: 1, 37: 1}
Posons, pour tout ![]() :
:
![]()
![]()
![]()
Conclusion : 0 est le seul entier ![]() pour lequel
pour lequel ![]() est premier.
est premier.

On rappelle (voir l’exercice n° 8 de la fiche n° 1 consacrée aux nombres premiers) que si ![]() et
et ![]() alors :
alors :
(![]() )
) ![]()
![Rendered by QuickLaTeX.com \[\boxed{\forall k\in\llbracket0,p-1\rrbracket,\,\binom{p-1}{k}\equiv\left(-1\right)^{k}\pmod{p}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-88d616f2188f063e9b83bbb7991e9298_l3.png)
- Pour
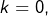 ok.
ok. - Supposons que
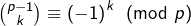 pour un certain
pour un certain 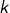 tel que
tel que 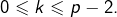 Alors, d’après la formule de Pascal :
Alors, d’après la formule de Pascal :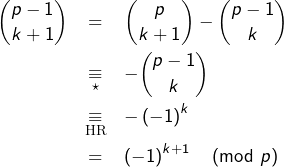
Noter qu’on a pu utiliser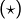 puisque
puisque 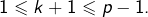

Posons :
![Rendered by QuickLaTeX.com \[A=\left(\prod_{i=1}^{n}p_{i}\right)-1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e6bea8714c9111dcc42b27d5c601e5cc_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{p_{n+1}<\prod_{i=1}^{n}p_{i}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d291bb9b3f9f522dead9f68ab1116f04_l3.png)
Si ![]() alors
alors ![]() convient, puisque :
convient, puisque :
![]()
Donc, d’après le petit théorème de Fermat :
![]()
![]()
![]()
![]()

D’après la formule de Legendre :
![Rendered by QuickLaTeX.com \[v_{p}\left(n!\right)=\sum_{k=1}^{\infty}\left\lfloor \frac{n}{p^{k}}\right\rfloor\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c27854ce39f254b8e7c39da5dd1aee8b_l3.png)
![]()
Comme ![]() pour tout
pour tout ![]() :
:
![Rendered by QuickLaTeX.com \[n\left(\sum_{k=1}^{n_{p}}\frac{1}{p^{k}}\right)-n_{p}<v_{p}\left(n!\right)\leqslant n\left(\sum_{k=1}^{n_{p}}\frac{1}{p^{k}}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bdaee3c8d6c825e90b8d4a1990d91674_l3.png)
![Rendered by QuickLaTeX.com \[\lim_{n\rightarrow\infty}\sum_{k=1}^{n_{p}}\frac{1}{p^{k}}=\frac{1}{p-1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-835e7e73b34e21a34327adeee49dd49d_l3.png)
![]()

Soit ![]() un nombre parfait pair, distinct de 6. On sait qu’il existe
un nombre parfait pair, distinct de 6. On sait qu’il existe ![]() tel que :
tel que :
![]()
- le cas
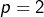 est exclu, puisque
est exclu, puisque 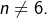
- si
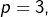 alors
alors 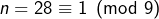
Et si ![]() alors
alors ![]() ou bien
ou bien ![]() ce qui conduit aux deux cas supplémentaires ci-dessous. On va utiliser le fait que :
ce qui conduit aux deux cas supplémentaires ci-dessous. On va utiliser le fait que :
(![]() )
) ![]()
![]()
- si
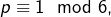 alors
alors 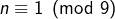 d’après
d’après 
- si
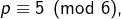 alors
alors 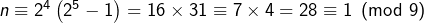 toujours d’après
toujours d’après 
On a bien établi que ![]()
Remarque
Comme tout entier naturel est congru modulo 9 à la somme de ses chiffres, ceci explique l’observation faite par Tartaglia (1506 – 1559) qu’en itérant le calcul de la somme des chiffres décimaux d’un nombre parfait pair, autre que 6, on aboutisse toujours à 1 :
![]()
![]()
![]()
![]()
![]()
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
