Solution pour le challenge 52
En expérimentant avec de petites valeurs de ![]() on conjecture que cette somme est égale à
on conjecture que cette somme est égale à ![]()
Posons donc :
![Rendered by QuickLaTeX.com \[x_{n}=\sum_{k=1}^{n}\,\frac{k\:k!}{n^{k+1}}\,\binom{n}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-54ce5b9bda777f4ac0604eab1ee2503e_l3.png)
Méthode 1 (proposée par Hervé CLAVIER, enseignant)
Pour tout ![]() :
:
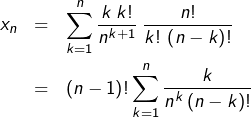
En posant
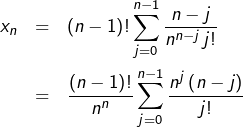
Or :
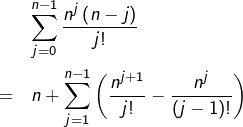
ce qui fait apparaître une sommation télescopique. Il reste après simplification :
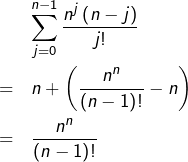
Méthode 2 (probabiliste)
On considère dans ce qui suit, une urne contenant ![]() boules numérotées de 1 à
boules numérotées de 1 à ![]() (avec
(avec ![]()
On effectue une succession de tirages d’une boule, avec remise, et l’on note ![]() la variable aléatoire indiquant le rang du tirage au cours duquel, pour la première fois, on obtient une boule déjà obtenue auparavant.
la variable aléatoire indiquant le rang du tirage au cours duquel, pour la première fois, on obtient une boule déjà obtenue auparavant.
Une boule donnée peut réapparaître dès le second tirage et, au plus tard, lors du ![]() -ème tirage. On voit donc facilement que l’ensemble des valeurs atteintes par
-ème tirage. On voit donc facilement que l’ensemble des valeurs atteintes par ![]() est :
est :
![]()
![]()
Si
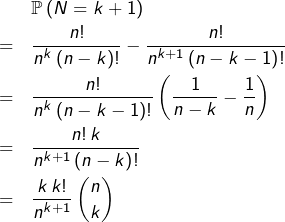
![]()
Au final, la relation :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\mathbb{P}\left(N=k+1\right)=1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-185e16cb2cf5fc580e7598350be59113_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^{n}\frac{k\thinspace k!}{n^{k+1}}\thinspace\binom{n}{k}=1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ef023295d26cc74934b8f40aeb5e49fd_l3.png)
Méthode 3 (un parfum de fonction 𝚪)
On sait (voir l’exercice n° 3 de cette fiche) que pour tout ![]() :
:
![]()
![]()
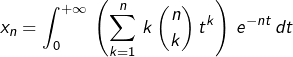
soit
![]()
On obtient :
![Rendered by QuickLaTeX.com \displaystyle{A_{n}=\underbrace{\left[-\left(1+t\right)^{n}\,e^{-nt}\right]_{t=0}^{+\infty}}_{=1}+n\,\int_{0}^{+\infty}\,\left(1+t\right)^{n-1}\,e^{-nt}\,dt}](https://math-os.com/wp-content/ql-cache/quicklatex.com-c30f29e3498897e975e8951e89eeee2b_l3.png)
et donc
Méthode 4 (une formule plus générale)
On commence par le :
Lemme
Etant donné un entier ![]() et des réels
et des réels ![]() :
: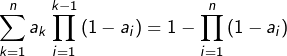
Note : on utilise la convention usuelle selon laquelle un produit indexé par l’ensemble vide est égal à 1.
Cette formule se prouve aisément par récurrence, ou bien en observant que la sommation peut être rendue télescopique. En effet, pour tout ![]() :
:
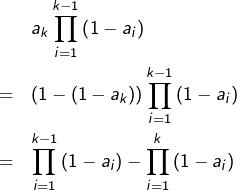
L’entier ![]() étant fixé, si l’on choisit
étant fixé, si l’on choisit
![]()
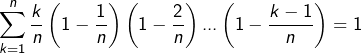
c’est-à-dire :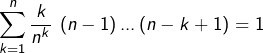
ou encore :
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^n\frac{k\,k!}{n^{k+1}}\binom{n}{k}=1}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-02dcaf4902b089cf4cd20f4b62c01c25_l3.png)
Pour consulter l’énoncé, c’est ici

