Question
Bonjour, j’ai un petit souci concernant une preuve en mathématiques, sur la combinatoire et le dénombrement. On doit prouver que le coefficient binomial du milieu est toujours le plus grand quel que soit n, je ne vois pas du tout comment faire ! Merci.
Réponse
Tout d’abord, cette question doit être légèrement reformulée puisque si ![]() est impair, il n’y a pas de « coefficient binomial du milieu » … il y en a plutôt deux dans ce cas, à savoir
est impair, il n’y a pas de « coefficient binomial du milieu » … il y en a plutôt deux dans ce cas, à savoir ![]() et
et ![]() Et il sont égaux, vue la propriété de symétrie, qui dit que pour tout
Et il sont égaux, vue la propriété de symétrie, qui dit que pour tout ![]() et pour tout
et pour tout ![]() :
:
![]()
Pour tout
![]()
- Pour
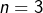 :
:![Rendered by QuickLaTeX.com \[L_3=\left[1,3,3,1\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-09191a5a6fcf8b2fee60f0e770f8a787_l3.png)
- Pour
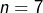 :
:![Rendered by QuickLaTeX.com \[L_7=\left[1,7,21,35,35,21,7,1\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0bdf95c8afba615e945181a7760da71f_l3.png)
- Pour
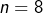 :
:![Rendered by QuickLaTeX.com \[L_8=\left[1,8,28,56,70,56,28,8,1\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4d65624aea10100c590a6ca1e15bbeb2_l3.png)
On procède avec la liste ![]() de la même manière que l’on étudie le sens de variation d’une suite. On peut s’intéresser au signe de la différence :
de la même manière que l’on étudie le sens de variation d’une suite. On peut s’intéresser au signe de la différence :
![]()
![Rendered by QuickLaTeX.com \[A_{n,k}=\frac{\binom{n}{k+1}}{\binom{n}{k}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e44c9db5b5f285303d0952a183fefa12_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{k\leqslant\left\lfloor\frac{n-1}{2}\right\rfloor}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a1a471ebb7283e74826c2f626e6296dc_l3.png)
Espérant avoir clarifié un peu les choses …


It’s a pity you don’t have a donate button! I’d most certainly donate to this excellent blog!
I guess for now i’ll settle for bookmarking and adding your RSS feed to my Google account.
I look forward to new updates and will talk about this site with my Facebook group.
Talk soon!