Question
Bonjour, je rentre en prépa scientifique à la rentrée 2019 et je fais des exercices pour m’entraîner. Je bute sur l’exercice suivant.
Résoudre dans ![]() l’équation :
l’équation :
![]()
Merci pour toute aide.
Réponse
L’idée, si possible, est d’obtenir un produit nul. (voir l’équation ![]() ci-dessous).
ci-dessous).
La formule générale :
![]()
![]()
L’équation proposée équivaut donc à :
![]()
ou encore à :
![]()
D’une part, les solutions de ![]() sont les réels de la forme :
sont les réels de la forme :
![]()
D’autre part, l’équation ![]() peut aussi s’écrire :
peut aussi s’écrire :
![]()
![Rendered by QuickLaTeX.com \[ \begin{array}{ccc} 2x & = & \frac{\pi}{6}+2k\pi\\ & \text{ou}\\ 2x & = & \pi-\frac{\pi}{6}+2k\pi \end{array}\qquad\text{avec }k\in\mathbb{Z}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-42ffb73b95d4f8bbabbbb7d9d1346c18_l3.png)
Finalement, l’ensemble des solutions dans ![]() est :
est :
![]()
Il reste à en extraire l’ensemble ![]() des solutions dans
des solutions dans ![]() Chacune des conditions :
Chacune des conditions :
![]()
![]()
et
![]()
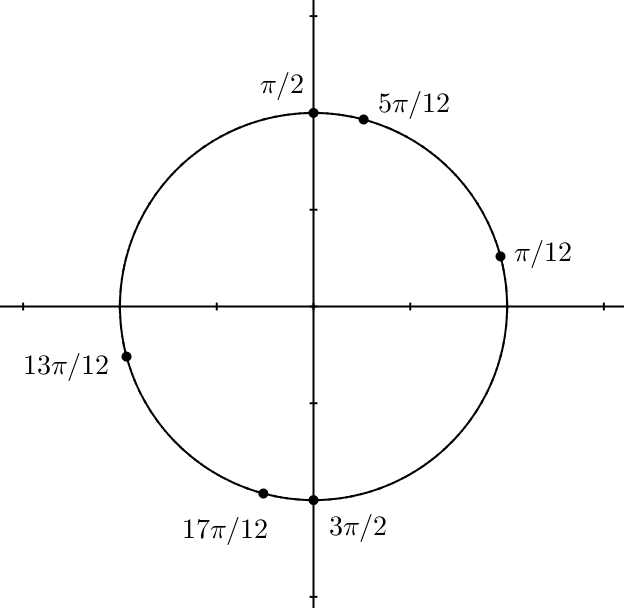
![Rendered by QuickLaTeX.com \[ \boxed{\mathcal{S}=\left\{\frac{\pi}{12},\frac{5\pi}{12},\frac{\pi}{2},\frac{13\pi}{12},\frac{17\pi}{12},\frac{3\pi}{2}\right\} }\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-441d46743e7d6e85654875a1efba68b1_l3.png)
On peut placer les solutions obtenues sur le cercle trigonométrique :