Question
On observe que :
![Rendered by QuickLaTeX.com \[2\times3\times\left(1+\frac{1}{2}\right)=3^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d87ce36b1d21ed99f4e188dec227be96_l3.png)
![Rendered by QuickLaTeX.com \[3\times4\times\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}\right)=5^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4cb1b2662c9603874e33bfe2a1d7e61e_l3.png)
![Rendered by QuickLaTeX.com \[4\times5\times\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}\right)=7^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-3a6f086a782034d5e0a95654156eb5d2_l3.png)
mais que :
![Rendered by QuickLaTeX.com \[5\times6\times\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}\right)\simeq81.53\neq9^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c9e5a8a9d78545b6756861009491d791_l3.png)
Pourquoi ?
Réponse
D’une manière générale, si l’on considère deux suites 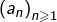 et
et 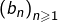 de nombres réels, le fait que ces deux suites coïncident pour les premières valeurs de l’indice
de nombres réels, le fait que ces deux suites coïncident pour les premières valeurs de l’indice 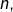 disons pour
disons pour 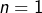 à
à 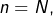 est une chose au fond assez banale, qui n’implique absolument pas que l’égalité
est une chose au fond assez banale, qui n’implique absolument pas que l’égalité 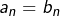 soit maintenue pour les indices plus grands que
soit maintenue pour les indices plus grands que 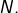
Dans votre exemple, les suites en question sont respectivement définies par :
![Rendered by QuickLaTeX.com \[a_{n}=\left(n+1\right)\left(n+2\right)\sum_{k=1}^{2n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-671dbd217f84e5fbbb87498a368a8691_l3.png)
et
![Rendered by QuickLaTeX.com \[b_{n}=\left(2n+1\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f8574cc30985d55a8bf9d96ab1475fab_l3.png)
Effectivement
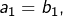
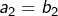
et
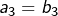
et nous aimerions peut-être que la fête continue au-delà … Mais il n’en est rien :
![Rendered by QuickLaTeX.com \[a_{4}=\frac{2283}{28}\neq9^{2}=b_{4}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-30ca1b0c5dd41b90d902a0db062c1768_l3.png)
Etant donné un entier
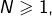
il n’est pas difficile de construire une suite
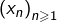
telle que :
![Rendered by QuickLaTeX.com \[\forall k\in\left\llbracket 1,N\right\rrbracket ,\thinspace x_{k}=\left(2k+1\right)^{2}\qquad\text{et}\qquad x_{N+1}\neq\left(2N+1\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d5a32cf9790f6665df4892ab45186d47_l3.png)
Il suffit d’utiliser un polynôme interpolateur de Lagrange (voir
cette vidéo). Par exemple, il existe un unique polynôme
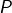
de degré
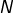
tel que :
![Rendered by QuickLaTeX.com \[\forall k\in\left\llbracket 1,N\right\rrbracket ,\thinspace P\left(k\right)=\left(2k+1\right)^{2}\qquad\text{et}\qquad P\left(N+1\right)=0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-4b192f6be40d6a62cfeaf9b8bc61a82a_l3.png)
Pour revenir à la question « pourquoi ? », voici un autre élément de réponse.
Notons, pour tout 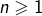 :
:
![Rendered by QuickLaTeX.com \[H_{n}=\sum_{k=1}^{n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1e9e62ff52597157f7ef82d4b070212a_l3.png)
Il n’est
pas possible qu’on ait, pour tout
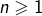
:
![Rendered by QuickLaTeX.com \[\left(n+1\right)\left(n+2\right)H_{2n}=\left(2n+1\right)^{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-60cb49bd8a44ed5acc4d78c1c0cbc681_l3.png)
En effet, on peut montrer que, lorsque
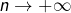
:
![Rendered by QuickLaTeX.com \[H_{n}\sim\ln\left(n\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e55ad96660fe72ac98ecb761a735dd2f_l3.png)
ce qui entraîne que :
![Rendered by QuickLaTeX.com \[\left(n+1\right)\left(n+2\right)H_{2n}\sim n^{2}\ln\left(2n\right)\sim n^{2}\ln\left(n\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-28126da6ddeaf3178121beb6363b1d3f_l3.png)
tandis que, évidemment :
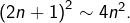
Il existe donc fatalement un rang
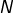
au-delà duquel les deux suites ne coïncident plus.
![]()
![]()
![]()
![]()
![]() et
et ![]() de nombres réels, le fait que ces deux suites coïncident pour les premières valeurs de l’indice
de nombres réels, le fait que ces deux suites coïncident pour les premières valeurs de l’indice ![]() disons pour
disons pour ![]() à
à ![]() est une chose au fond assez banale, qui n’implique absolument pas que l’égalité
est une chose au fond assez banale, qui n’implique absolument pas que l’égalité ![]() soit maintenue pour les indices plus grands que
soit maintenue pour les indices plus grands que ![]()
![Rendered by QuickLaTeX.com \[a_{n}=\left(n+1\right)\left(n+2\right)\sum_{k=1}^{2n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-671dbd217f84e5fbbb87498a368a8691_l3.png)
![]()
![]()
![]()
![]()
![]() :
:![Rendered by QuickLaTeX.com \[H_{n}=\sum_{k=1}^{n}\frac{1}{k}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1e9e62ff52597157f7ef82d4b070212a_l3.png)
![]()
![]()
![]()


Oui, je m’en suis rendu compte en réfléchissant 2 secondes… J’ai un peu honte, sur le coup. J’ai beau être agrégé, j’enseigne au collège depuis tellement longtemps, que j’ai perdu l’essentiel de mes neurones ! C’est pour ça que je me suis contraint à faire des colles en prépa depuis quelques années. Bonne journée à vous.
OK, je n’ai rien dit. C’est équivalent au deux, mais ln(n) est un équivalent plus simple. Dure la rentrée…
C’est plutôt ln(2n) à l’avant-dernière ligne, non ?
A priori, oui. Mais il se trouve que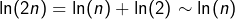 , donc c’est correct. Je vais toutefois détailler.
, donc c’est correct. Je vais toutefois détailler.