Question
Je sais prouver par récurrence que :
![Rendered by QuickLaTeX.com \[\forall n\in\mathbb{N}^\star,\quad\sum_{k=1}^{n}k^2=\frac{n(n+1)(2n+1)}{6}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c71e571b94fa0388d958af1fe7246f32_l3.png)
Mais comment se douter de la réponse si elle ne nous est pas donnée par l’énoncé ?
Réponse
Bonne question ! Pour établir une propriété par récurrence, encore faut-il savoir quelle est cette propriété…
Voici une méthode astucieuse (mais très classique) qui a en outre le mérite de se généraliser. On introduit la somme :
![Rendered by QuickLaTeX.com \[Q_n=\sum_{k=1}^{n}\left[(k+1)^3-k^3\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a1ae4f056a1a31e781b4ebefb0e948e3_l3.png)
et on la calcule de deux façons.
D’une part, il s’agit d’une sommation télescopique, ce qui signifie que les termes se simplifient mutuellement, à l’exception :
- du terme
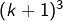 pour
pour 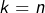
- et du terme
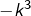 pour
pour 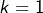 .
.
Ainsi :
![]()
D’autre part, on peut développer le terme général de cette somme : ![]() . Il s’ensuit que :
. Il s’ensuit que :
![Rendered by QuickLaTeX.com \[Q_n=3\sum_{k=1}^nk^2+3\sum_{k=1}^nk+\sum_{k=1}^n1=3\sum_{k=1}^nk^2+\frac{3n(n+1)}2+n\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bdb627a09afdf7f8d1e00b1a95f6da7a_l3.png)
En confrontant les deux formules obtenues, il apparaît que :
![Rendered by QuickLaTeX.com \[\sum_{k=1}^nk^2=\frac13\left[(n+1)^3-1-\frac{3n(n+1)}2-n\right]\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9a538b8d9c9d7f0928e2f9da5711ac16_l3.png)
et il ne reste plus qu’à simplifier ceci (en commençant par mettre ![]() en facteur) pour obtenir la formule :
en facteur) pour obtenir la formule :
![Rendered by QuickLaTeX.com \[\boxed{\sum_{k=1}^nk^2=\frac{n(n+1)(2n+1)}6}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2466e1d38a336903db4dbcfc84707295_l3.png)
Pour approfondir la question, je vous suggère cette vidéo.

