Lettre E

EMBOITÉS (intervalles)

Si l’on considère une suite $\left(I_{k}\right)_{k\geqslant0}$ d’intervalles, décroissante pour l’inclusion (c’est-à-dire vérifiant $I_{k+1}\subset I_{k}$ pour tout $k\in\mathbb{N}),$ et si l’on intersecte tous les $I_{k},$ l’ensemble obtenu est un intervalle. Mais celui-ci peut être vide :

c’est le cas si, par exemple, 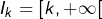$I_{k}=\left[k,+\infty\right[$ pour tout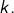 $k.$
c’est aussi le cas lorsque $I_{k}=\left]0,2^{-k}\right]$ pour tout $k.$

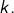
Dans le premier cas, les intervalles sont tous fermés. Dans le second, la longueur de $I_{k}$ tend vers 0. Mais aucune de ces conditions ne suffit pour empêcher l’intersection d’être vide.

Maintenant, combinons les deux hypothèses :

Théorème (des segments emboîtés) n° 1

Si $\left(I_{k}\right)_{k\geqslant0}$ est une suite de segments (intervalles fermés et bornés, non triviaux), décroissante pour l’inclusion et si la longueur de $I_{k}$ tend vers 0 lorsque $k$ tend vers l’infini, alors il existe un réel $\lambda$ tel que :

$\bigcap_{k=0}^{\infty}I_{k}=\left\{ \lambda\right\}$

Si l’on pose $I_{k}=\left[a_{k},b_{k}\right],$ alors les suites $a$ et $b$ sont adjacentes (la suite $a$ est croissante, la suite $b$ est décroissante et leur différence tend par hypothèse vers 0). Elles ont donc une limite commune $\lambda.$ Comme $a_{k}\leqslant\lambda\leqslant b_{k}$ pour tout $k,$ alors $\lambda$ appartient à l’intersection de tous les $I_{k}.$

Et si $\mu$ appartient à cette intersection, alors en passant à la limite dans l’encadrement $a_{k}\leqslant\mu\leqslant b_{k},$ on voit que $\mu=\lambda.$

Ce résultat permet par exemple d’établir le théorème de Bolzano-Weierstrass dans le champ réel : de toute suite réelle bornée, on peut extraire une sous-suite convergente.

On peut généraliser le théorème 1 : dans un espace métrique complet, l’intersection d’une suite décroissante de parties fermées, non vides, dont le diamètre tend vers 0 est un singleton. Voir cet article.

En abandonnant la condition portant sur la longueur des $I_{k},$ on obtient le résultat suivant :

Théorème (des segments emboîtés) n° 2

Si $\left(I_{k}\right)_{k\geqslant0}$ est une suite de segments (intervalles fermés et bornés non triviaux), décroissante pour l’inclusion, alors :

$\bigcap_{k=0}^{\infty}I_{k}\text{ est un intervalle fermé, borné et \textbf{non vide}}$

Seul le caractère non vide de l’intersection mérite une explication.

On peut définir une suite $a$ en choisissant un terme $a_{k}$ dans $I_{k}$ et ceci pour tout $k\in\mathbb{N}.$

Cette suite est à termes dans $I_{0}$ donc est bornée. D’après Bolzano-Weierstrass, on peut en extraire une sous-suite convergente $\left(a_{\varphi\left(n\right)}\right)_{n\in\mathbb{N}}.$ Notons $\lambda$ sa limite.

Pour tout $n\in\mathbb{N},$ la suite tronquée $\left(a_{\varphi\left(k\right)}\right)_{k\geqslant n}$ est à termes (dans $I_{\varphi\left(n\right)}$ donc) dans $I_{n}$ qui est fermé. Par conséquent $\lambda\in I_{n}.$ Ceci prouve que $\lambda$ appartient à l’intersection des $I_{n},$ qui est de ce fait non vide.

Là encore, le résultat se généralise : dans un espace métrique, l’intersection d’une suite décroissante de parties compactes non vides est non vide.

ÉQUIVALENTS (règle des)

Pour les séries

Soient deux séries $\sum u_n$ et $\sum v_n$ à termes positifs.

Si $u_n\sim v_n$ alors les deux séries sont de même nature.

La positivité à partir d’un certain rang suffit. En outre, on sait que l’équivalence préserve localement le signe : donc si $u_n\sim v_n$ et si $v_n>0$ APCR, alors $u_n>0$ APCR.

En pratique, il suffit donc (en plus de l’équivalent) de s’assurer que l’une des deux suites est de signe constant APCR.

Sans la condition de signe, cette règle n’est plus valide. Par exemple :

$\frac{(-1)^n}{\sqrt n}\sim\frac{(-1)^n}{\sqrt n}+\frac{1}{n}$

Pourtant la série alternée $\sum_{n\geqslant 1}\frac{(-1)^n}{\sqrt n}$ converge, tandis que l’autre diverge (somme d’une série convergente et de la série harmonique, qui diverge).

Exemples

La série

$\boxed{\sum_{n\geqslant1}\frac{e-\left(1+\frac1n\right)^n}{\sqrt{n^2+n+1}}}$

converge puisque :

$\frac{e-\left(1+\frac1n\right)^n}{\sqrt{n^2+n+1}}\sim\frac{e}{2n^2}$

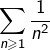et la série de Riemann $\displaystyle{\sum_{n\geqslant1}\frac{1}{n^2}}$ converge.

La série

$\boxed{\sum_{n\geqslant1}\sin\left(\frac{1}{\sqrt n}\right)\ln\left(n+\sin(n)\right)}$

diverge puisque :

$\sin\left(\frac{1}{\sqrt n}\right)\ln\left(n+\sin(n)\right)\sim\frac{\ln(n)}{\sqrt n}$

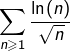et la série de Bertrand $\displaystyle{\sum_{n\geqslant1}\frac{\ln(n)}{\sqrt n}}$ diverge.

Pour les intégrales

Soient deux applications continues et positives $f,g:[0,+\infty[\to\mathbb{R}$ .

Si $f(t)\underset{+\infty}{\sim}g(t)$ , alors les intégrales impropres $\int_0^{+\infty}f(t)\,dt$ et $\int_0^{+\infty}g(t)\,dt$ sont de même nature.

Mêmes remarques que pour les séries – en s’adaptant, bien sûr, au contexte. Par souci de simplicité, la règle ci-dessus a été formulée pour des intégrales de fonctions continues positives sur $[0,+\infty[$ , mais on dispose d’énoncés analogues si l’intervalle d’intégration est par exemple $[a,b[$ , les intégrales étant impropres pour la borne $b$ .

Exemples

L’intégrale

$\boxed{\int_0^{+\infty}\frac{t}{\sqrt{t^4+1}}\,dt}$

diverge puisque :

$\frac{t}{\sqrt{t^4+1}}\underset{+\infty}{\sim}\frac{1}{t}$

et l’intégrale impropre $\displaystyle{\int_1^{+\infty}\frac{1}{t}\,dt}$ diverge.

L’intégrale

$\boxed{\int_0^1\frac{\ln(t)}{\left(1-t\right)^{3/2}}\,dt}$

est doublement impropre. Elle converge car, d’une part

$\frac{\ln(t)}{\left(1-t\right)^{3/2}}\underset{0}{\sim}\ln(t)$

et l’intégrale impropre

$\int_0^{1/2}\ln(t)\,dt$

converge et, d’autre part :

$\frac{\ln(t)}{\left(1-t\right)^{3/2}}\underset{1}{\sim}-\frac{1}{\sqrt{1-t}}$

et l’intégrale impropre

$\int_{1/2}^1\frac{1}{\sqrt{1-t}}\,dt$

converge

EUCLIDE (lemme d’)

Il s’agit du résultat suivant (qui apparaît dans les éléments d’Euclide – livre VII, proposition 32) :

Lemme d’Euclide

Etant donné un nombre premier $p$ et deux entiers $a,b\in\mathbb{N}^{\star},$ si $p\mid ab$ alors $p\mid a$ ou $p\mid b.$

On peut voir ce résultat comme corollaire du théorème de Gauss, quoique ce point de vue soit franchement anachronique (environ deux millénaires séparent Euclide de Gauss !).

En voici une preuve directe :

Preuve (cliquer pour déplier / replier)

Soient $p\in\mathbb{P}$ et $a,b\in\mathbb{N}^{\star}$ tels que $p\mid ab.$

Raisonnons par l’absurde et supposons que $p\nmid a$ et $p\nmid b.$

L’ensemble

$E=\left\{ B\in\mathbb{N}^{\star};\thinspace p\mid aB\text{ et }p\nmid B\right\}$

est non vide (il contient $b)$ donc admet un plus petit élément $\beta.$

On observe que $\beta\neq1$ (puisque $p\nmid a).$

Par ailleurs, supposons un instant que $\beta\geqslant p.$ Effectuons la division euclidienne de $\beta$ par $p$ :

$\beta=pq+\beta'\qquad\text{avec : }\left\{\begin{array}{c}0\leqslant\beta'<p\\q\geqslant1\end{array}\right.$

Vu que $p\mid a\beta'$ (car $a\beta'=a\beta-apq$ et $p\mid a\beta$ par hypothèse) et que $p\nmid\beta'$ (car sinon $p\mid\beta,$ ce qui est exclu vu que $\beta\in E),$ on obtient une contradiction avec la minimalité de $\beta$ (puisque $0<\beta'=\beta-pq<\beta$ ). Donc :

( $\star$ ) $\boxed{1<\beta<p}$

Pour finir, effectuons la division euclidienne de $p$ par $\beta$ :

$p=\beta Q+r\qquad\text{avec : }0\leqslant r<\beta$

Nécessairement $r\neq0$ car sinon $\beta$ serait un diviseur non trivial de $p$ (cf. $\star),$ or $p$ est premier.

En outre $ar=ap-a\beta Q$ donc $p\mid ar$ et $p\nmid r$ (car $0<r<p)$ .

Ceci contredit la minimalité de $\beta.$

L’hypothèse initiale ne tient donc pas : on a prouvé que $p\mid a$ ou $p\mid b.$

EULER (constante d’)

En désignant par $H_{n}$ le $n-$ ème nombre harmonique :

$H_{n}=\sum_{k=1}^{n}\dfrac{1}{k}$

on peut montrer que la suite de terme général $x_{n}=H_{n}-\ln\left(n\right)$ est décroissante et minorée, donc convergente. Sa limite est appelée la constante d’Euler et notée $\gamma$ :

$\boxed{\gamma=\lim_{n\rightarrow+\infty}\left(1+\dfrac{1}{2}+\cdots+\dfrac{1}{n}-\ln\left(n\right)\right)}$

Voici une valeur approchée de $\gamma$ à $10^{-15}$ près :

$\gamma\simeq0.57721566490153$

Il est conjecturé de $\gamma$ est un nombre irrationnel, mais cette question est encore ouverte à ce jour. Voici quatre « jolies » formules faisant intervenir la constante d’Euler :

$\int_{0}^{1}\left(\dfrac{1}{t}-\left\lfloor \dfrac{1}{t}\right\rfloor \right)\thinspace dt=1-\gamma$

$\gamma=\dfrac{\ln\left(2\right)}{2}+\dfrac{1}{\ln\left(2\right)}\sum_{n=2}^{\infty}\dfrac{\left(-1\right)^{n}\ln\left(n\right)}{n}$

$\int_{0}^{x}\dfrac{1-\cos\left(t\right)}{t}\thinspace dt\underset{{\scriptstyle +\infty}}{=}\ln\left(x\right)+\gamma+o\left(1\right)$

$\lim_{n\rightarrow+\infty}\ln\left(n\right)\prod_{p\leqslant n}\left(1-\dfrac{1}{p}\right)=e^{-\gamma}$

Dans cette dernière égalité, le produit est indexé par les nombres premiers inférieurs ou égaux à $n.$ Pour en savoir plus sur la constante d’Euler, on pourra consulter cette vidéo :

EXTRAITE (suite)

Considérons une suite $u=\left(u_{n}\right)_{n\geqslant0}$ à termes dans un ensemble $X$ (non vide, mais à part cela quelconque).

Toute suite de la forme $\left(u_{f\left(n\right)}\right)_{n\geqslant0},$ où $f:\mathbb{N}\rightarrow\mathbb{N}$ est strictement croissante, est appelée suite extraite (ou sous-suite) de $u.$

Si l’imagine les termes $u_{0},$ $u_{1},$ $u_{2},$ etc … disposés devant nous, il s’agit d’en sélectionner une infinité, en piochant toujours plus loin et sans retour en arrière possible.

Par exemple, les suites $\left(u_{2n}\right)_{n\geqslant0},$ $\left(u_{n^{2}}\right)_{n\geqslant0}$ et $\left(u_{2^{n}}\right)_{n\geqslant0}$ sont extraites de $u.$ Mais ce n’est pas le cas de la suite $\left(u_{n+\left(-1\right)^{n}}\right)_{n\geqslant0}$ puisque l’application $\mathbb{N}\rightarrow\mathbb{N},\thinspace n\mapsto n+\left(-1\right)^{n}$ n’est pas croissante.

Supposons désormais que $X=\mathbb{R}.$ On appelle valeur d’adhérence de la suite $u$ la limite d’une suite extraite convergente.

Il est facile de voir que toute suite convergente possède une seule valeur d’adhérence (sa limite) mais que, réciproquement, une suite possédant une seule valeur d’adhérence n’est pas nécessairement convergente (un contre-exemple : la suite de terme général $u_n=0$ si n est pair et $u_n=n$ sinon).

Une suite réelle ne possède pas nécessairement de valeur d’adhérence (penser à la suite de terme général $u_{n}=n).$ Cependant :

Théorème (Bolzano-Weierstrass)

De toute suite réelle bornée, on peut extraire une sous-suite convergente.

Pour une preuve, voir par exemple l’exercice n° 9 de cette fiche.

Signalons encore qu’étant donnée une suite réelle $u,$ l’ensemble $V$ de ses valeurs d’adhérence est une partie fermée de $\mathbb{R}.$ En effet, si l’on note pour tout $n\in\mathbb{N}$ :

$X_{n}=\left\{ x_{k};\thinspace k\geqslant n\right\}$

alors :

$V=\bigcap_{n=0}^{\infty}\overline{X_{n}}$

Ceci montre que $V$ est fermé, puisque c’est l’intersection d’une famille de fermés. Pour finir, si la suite réelle $u$ est bornée alors :

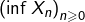la suite $\left(\inf X_{n}\right)_{n\geqslant0}$ est croissante et converge vers la plus petite valeur d’adhérence de 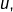$u,$ qu’on note 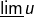$\underline{\lim}u$ (lire : limite inférieure de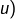 $u)$
la suite 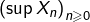$\left(\sup X_{n}\right)_{n\geqslant0}$ est décroissante et converge vers la plus grande valeur d’adhérence de 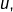$u,$ qu’on note 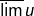$\overline{\lim}u$ (lire : limite supérieure de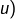 $u)$

Voir à ce sujet l’exercice n° 8 de cette fiche.

Partager cet article