Indications - Exercices de calcul de sommes - 02

Indications pour démarrer les exercices sur les calculs de sommes (fiche 02).
Cliquer ici pour accéder aux énoncés.

On peut minorer une somme de nombre réels par le produit $N\times P$ , où :

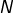$N$ désigne le nombre de termes
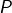$P$ désigne le plus petit terme

On peut tout à fait calculer $C_{n}$ pour de petites valeurs de $n,$ ce qui permet de conjecturer une formule générale que l’on établit ensuite par récurrence. C’est ce qui est fait à l’exercice n° 7 de cette fiche d’exercices.
On demande ici d’envisager une approche différente. Avez-vous essayé de regrouper les termes deux par deux ?

Si l’on connaît les expressions simplifiées pour chacune des sommes

$\sum_{k=1}^{n}1,\quad\sum_{k=1}^{n}k},\quad\sum_{k=1}^{n}k^{2}\quad\text{et}\quad\sum_{k=1}^{n}k^{3}$

alors il n’y a qu’à développer le produit $k\left(k+1\right)\left(k+2\right),$ séparer la somme en quatre et calculer, calculer … sans oublier de factoriser à la fin !

Faisable, mais franchement pas drôle…

Il existe une solution plus élégante, qui consiste à rendre la sommation télescopique.

Une somme de nombres réels est certainement majorée par le produit $n\times M$ , où $n$ et $M$ désignent respectivement le nombre de termes et le plus grand terme.

Utiliser l’identité de Cassini (voir par exemple ici) pour transformer la somme partielle de cette série et faire apparaître une sommation télescopique.

On pourra trouver une source d’inspiration dans cette vidéo

Utiliser l’inégalité entre moyennes géométrique et arithmétique pour $n$ réels positifs. On rappelle que si $t_{1},\cdots,t_{n}>0$ alors :

$\left(\prod_{k=1}^{n}t_{k}\right)^{1/n}\leqslant\frac{1}{n}\sum_{k=1}^{n}t_{k}$

Pour une preuve, voir par exemple cet article

Pour $A\subset E$ fixée, les parties $B$ de $E$ vérifiant $A\subset B$ sont de la forme $A\cup X$ avec $X\subset E-A.$

Il existe donc autant de telles parties $B$ que de parties de $E-A.$

Or, on sait que si $\text{card}\left(A\right)=k,$ alors $E-A$ possède $2^{n-k}$ sous-ensembles.

La variable aléatoire $X$ peut prendre toutes les valeurs entières comprises entre $n+1$ et $2n+1$ (inclusivement).

Etant donné $k\in\left{ 0,\cdots,n\right} ,$ dans quelles circonstances précises l’événement $\left(X=n+k+1\right)$ se réalise-t-il ?

Partager cet article