Solutions détaillées de neuf exercices sur les suites numériques (fiche 03).
Cliquer ici pour accéder aux énoncés.

Pour tout réel ![]() :
: ![]() Donc, pour tout
Donc, pour tout ![]() :
:
![]()
La suite proposée est donc périodique. Plus précisément, elle est constante si ![]() (c’est-à-dire si
(c’est-à-dire si ![]() et elle est 2-périodique sinon.
et elle est 2-périodique sinon.

Pour tout ![]() :
:
![]()
![Rendered by QuickLaTeX.com \[S_{n}=\sum_{k=1}^{n}\frac{c_{k}}{2^{k}}\leqslant9\thinspace\sum_{k=1}^{n}\frac{1}{2^{k}}<9\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-f0762e9c125b80ff28bf57c287446a0e_l3.png)
![Rendered by QuickLaTeX.com \[\sum_{k=1}^{n}\frac{1}{2^{k}}=\frac{1}{2}\:\frac{1-\frac{1}{2^{n}}}{1-\frac{1}{2}}=1-\frac{1}{2^{n}}<1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5c799f15093ca9660ac2e6e69a5cc29d_l3.png)
Si l’on pose ![]() pour tout
pour tout ![]() alors :
alors :
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{ccc}A & = & \ln\left(a\right)\\\frac{A}{2}+B\frac{\sqrt{3}}{2} & = & 2\ln\left(b\right)\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ab72b3cb4a3e4b8687b7d32d2e3cc0f8_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{x_{n}=R_{n}^{1/2^{n}}}\quad\text{avec}\quad\boxed{R_{n}=\left\{ \begin{array}{ccc}a & \text{si} & n\equiv0\pmod{6}\\\\b^{2} & \text{si} & n\equiv1\pmod{6}\\\\\frac{b^{2}}{a} & \text{si} & n\equiv2\pmod{6}\\\\\frac{1}{a} & \text{si} & n\equiv3\pmod{6}\\\\\frac{1}{b^{2}} & \text{si} & n\equiv4\pmod{6}\\\\\frac{a}{b^{2}} & \text{si} & n\equiv5\pmod{6}\end{array}\right.}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-c51f979950b7736024cf3a0becfffefc_l3.png)

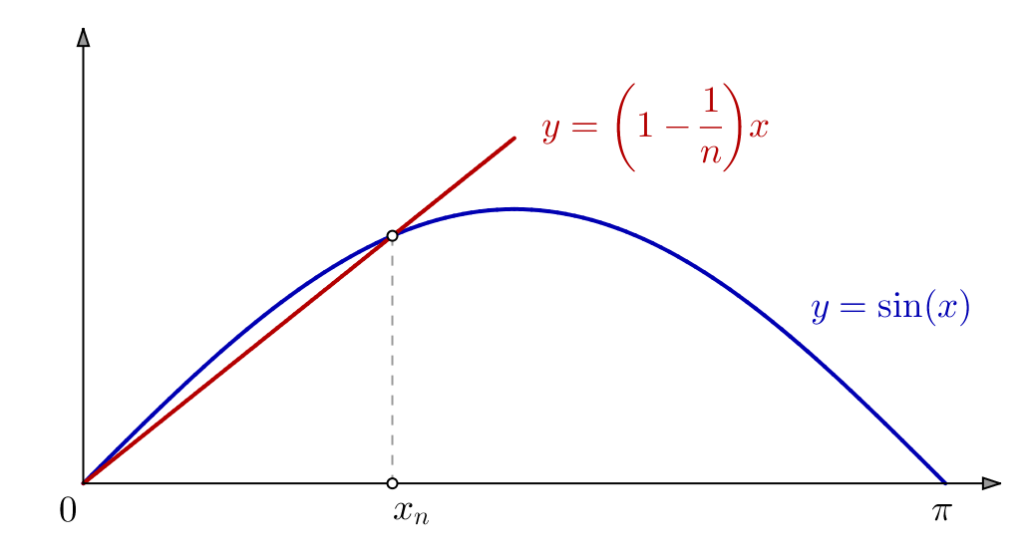
La figure ci-dessous montre ce qui se passe … La droite rouge courbe l’arche de sinusoïde en deux points : l’origine (qui ne nous intéresse pas) et un point dont on devine que l’abscisse ![]() va se rapprocher de plus en plus de 0, au fur et à mesure que n augmente. Il faut maintenant établir cela de manière rigoureuse !
va se rapprocher de plus en plus de 0, au fur et à mesure que n augmente. Il faut maintenant établir cela de manière rigoureuse !
Considérons l’application
![Rendered by QuickLaTeX.com \[\varphi:\left[0,\pi\right]\rightarrow\left[0,1\right],\thinspace x\mapsto\left\{ \begin{array}{cc}\frac{\sin\left(x\right)}{x} & \text{si }x\in\left]0,\pi\right]\\\\1 & \text{si }x=0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-dcb27b6a2a5e4641c3ce594aae166fe4_l3.png)
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{x_{n}\sim\sqrt{\frac{6}{n}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-aa5cbae8bca6725ce1b12563b092a7a3_l3.png)
Détail (cliquer pour déplier / replier)
L’application ![]() est dérivable et, pour tout
est dérivable et, pour tout ![]() :
:
![]()
![]()
Preuve (cliquer pour déplier / replier)
En effet, si ![]() alors pour tout
alors pour tout ![]() :
:
![]()
On procède de la même manière pour la borne ![]()
Comme ![]() il s’ensuit que
il s’ensuit que ![]() et donc
et donc ![]() décroît strictement sur
décroît strictement sur ![]()
Enfin, ![]() se prolonge en une application continue et strictement décroissante sur
se prolonge en une application continue et strictement décroissante sur ![]() Cette dernière induit une bijection de
Cette dernière induit une bijection de ![]() sur
sur ![]() notée
notée ![]()

La fonction ci-dessous renvoie la liste des ![]() premiers termes de la suite définie par :
premiers termes de la suite définie par :
![Rendered by QuickLaTeX.com \[u_{0}=s\qquad\text{et}\qquad\forall n\in\mathbb{N},\,u_{n+1}=\left\{ \begin{array}{cc}u_{n}\thinspace/\thinspace2 & \textrm{si }u_{n}\textrm{ est pair}\\\\u_{n}+5 & \textrm{sinon}\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7f4d8d899c981e3339924a2172a8a241_l3.png)
def suite(s,n):
seq = []
count = 0
t = s
while (count < n):
seq.append (t)
if (t % 2 == 0):
t = t // 2
else:
t += 5
count += 1
return seqPar exemple :
>>> suite (100,7)
[100, 50, 25, 30, 15, 20, 10]Si ![]() la suite est périodique. Il se forme en effet un cycle de longueur 6 :
la suite est périodique. Il se forme en effet un cycle de longueur 6 :
![]()
Si ![]() il se forme un cycle de longueur
il se forme un cycle de longueur ![]() :
:
![]()
Notons désormais ![]() l’ensemble des entiers
l’ensemble des entiers ![]() pour lesquels
pour lesquels ![]() pour un certain
pour un certain ![]() et montrons que
et montrons que ![]() Ceci prouvera que, quelle que soit la valeur de
Ceci prouvera que, quelle que soit la valeur de ![]() l’itération débouche tôt ou tard sur l’un des deux cycles précédents.
l’itération débouche tôt ou tard sur l’un des deux cycles précédents.
Raisonnons par récurrence et supposons que, pour un certain ![]() on ait :
on ait : ![]()
- Si
 est pair, alors
est pair, alors 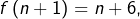 donc
donc 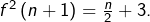 Comme
Comme 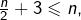 alors
alors 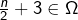 et donc
et donc 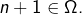
- Si
 est impair, alors
est impair, alors 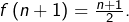 Mais
Mais 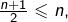 et donc
et donc 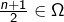 d’où à nouveau :
d’où à nouveau : 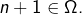
Ainsi ![]() et en conclusion :
et en conclusion : ![]()

On calcule, pour tout entier ![]() :
:
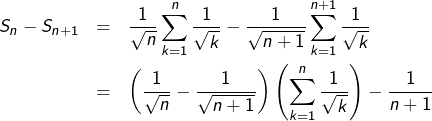
![]()
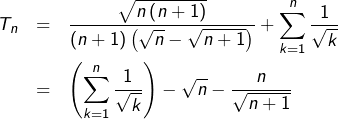
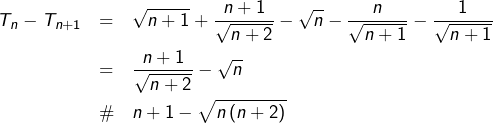
Ainsi la suite ![]() est décroissante. Et comme
est décroissante. Et comme ![]() alors
alors ![]() pour tout
pour tout ![]() Finalement, la suite
Finalement, la suite ![]() est croissante.
est croissante.
Remarque
On peut montrer que 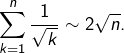 Il en résulte que
Il en résulte que ![]() converge vers
converge vers ![]()
La moyenne arithmétique des distances de 1 aux autres racines ![]() èmes de l’unité est :
èmes de l’unité est :
![Rendered by QuickLaTeX.com \[D_{n}=\frac{1}{n-1}\sum_{k=1}^{n-1}\left|1-e^{2ik\pi/n}\right|\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-16139c15016f1dae39dc38ac37f266dc_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \[\boxed{D_{n}=\frac{2}{n-1}\,\sum_{k=0}^{n-1}\,\sin\left(\frac{k\pi}{n}\right)}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e42d1b790649f87dc36d7a6ca20c5e88_l3.png)
![Rendered by QuickLaTeX.com \[R_{n}=\frac{1}{n}\sum_{k=1}^{n}\sin\left(\frac{k\pi}{n}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-0753510ee130176591e1dc001b3825a4_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\boxed{{\displaystyle \lim_{n\rightarrow+\infty}D_{n}=\frac{4}{\pi}}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-79c3fe5f784367580fbed85702b3d605_l3.png)

La suite ![]() est majorée (par 0) mais ne possède aucune valeur d’adhérence (elle diverge vers
est majorée (par 0) mais ne possède aucune valeur d’adhérence (elle diverge vers ![]() et chacune de ses suites extraites fait donc de même).
et chacune de ses suites extraites fait donc de même).
Soit maintenant ![]() une suite réelle bornée. Notons
une suite réelle bornée. Notons ![]() un majorant et
un majorant et ![]() un minorant de cette suite.
un minorant de cette suite.
Pour tout ![]() l’ensemble
l’ensemble ![]() est une partie de
est une partie de ![]() non vide et majorée (par
non vide et majorée (par ![]() ce qui autorise à considérer sa borne supérieure
ce qui autorise à considérer sa borne supérieure ![]() La suite
La suite ![]() est décroissante pour l’inclusion (ce qui signifie que
est décroissante pour l’inclusion (ce qui signifie que ![]() donc la suite
donc la suite ![]() est décroissante. Comme cette dernière est minorée (par
est décroissante. Comme cette dernière est minorée (par ![]() elle converge. Notons
elle converge. Notons ![]() sa limite.
sa limite.
On sait que l’ensemble des valeurs d’adhérence de ![]() est :
est :
![]()
Par conséquent, comme ![]() est un fermé :
est un fermé : ![]() pour tout
pour tout ![]() ce qui montre que
ce qui montre que ![]()
Il reste à montrer que ![]() est la plus grande valeur d’adhérence de
est la plus grande valeur d’adhérence de ![]() Pour cela, considérons une valeur d’adhérence
Pour cela, considérons une valeur d’adhérence ![]() Pour tout
Pour tout ![]()
![]() et donc
et donc ![]() (d’une manière générale, une partie non vide et majorée de
(d’une manière générale, une partie non vide et majorée de ![]() et son adhérence ont la même borne supérieure). En passant à la limite, on obtient :
et son adhérence ont la même borne supérieure). En passant à la limite, on obtient : ![]() comme souhaité.
comme souhaité.

Admettons que la suite ![]() soit bornée et soit
soit bornée et soit ![]() tel que :
tel que :
![]()
![]()
![Rendered by QuickLaTeX.com \[ z_{n}=z_{0}+\sum_{k=0}^{n-1}\left(z_{k+1}-z_{k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-189ee87d8187e5b5279947e2e99a11f2_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \[\mu_{n}\leqslant\mu_{1}\prod_{k=1}^{n-1}\left(1+r^{k}\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fdade8ca450c9939b34f8ac3e649252d_l3.png)
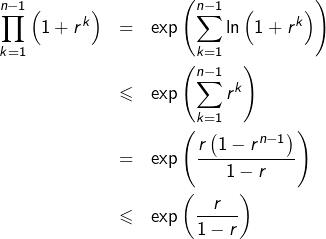
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.

