Solutions détaillées de neuf exercices sur le second degré (fiche 02).
Cliquer ici pour accéder aux énoncés.


On note ![]() les ensembles de solutions.
les ensembles de solutions.
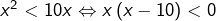 donc :
donc :![Rendered by QuickLaTeX.com \[\boxed{S_1=\left]0,10\right[}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-596b10a3f66af8cce3204a16f3cb2590_l3.png)
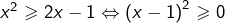 donc :
donc :![Rendered by QuickLaTeX.com \[\boxed{S_2=\mathbb{R}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-484b8de4151b468876370b6d40181c71_l3.png)
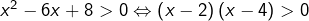 donc :
donc :![Rendered by QuickLaTeX.com \[\boxed{S_3=\left]-\infty,2\right[\cup\left]4,+\infty\right[}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fba41f225b1d7e73694030e1b034ce55_l3.png)
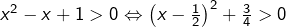 donc :
donc :![Rendered by QuickLaTeX.com \[\boxed{S_4=\mathbb{R}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-8787868cc3c3a7517a17edc06247e79e_l3.png)
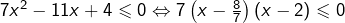 donc :
donc :![Rendered by QuickLaTeX.com \[\boxed{S_5=\left[\frac{8}{7},2\right]}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-90ff3cb7c80b4f86beb478e526437b04_l3.png)
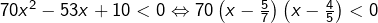 donc :
donc :![Rendered by QuickLaTeX.com \[\boxed{S_6=\left]\frac{5}{7},\frac{4}{5}\right[}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-19acd16f02d04a9e7a7cf26f4c97414e_l3.png)

C’est dès le début que tout va mal dans cette résolution : on ne peut pas effectuer les produits en croix dans une inéquation sans information sur les signes des dénominateurs !
Si l’on sait que ![]() et
et ![]() désignent deux réels non nuls et de même signe, alors pour tout couple
désignent deux réels non nuls et de même signe, alors pour tout couple ![]() de réels :
de réels :
![]()
Mais si par exemple ![]() et
et ![]() alors cette équivalence cesse d’être vraie.
alors cette équivalence cesse d’être vraie.
A présent, résolvons l’inéquation proposée.
Pour tout ![]() :
:
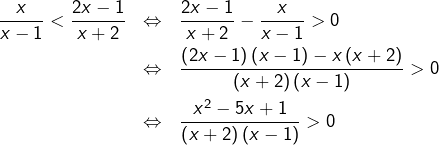
Le trinôme
![]()
D’une part, ![]() donc
donc ![]()
D’autre part, ![]() et
et ![]() donc
donc ![]()
En posant aussi ![]() on peut construire le tableau de signe ci-dessous :
on peut construire le tableau de signe ci-dessous :
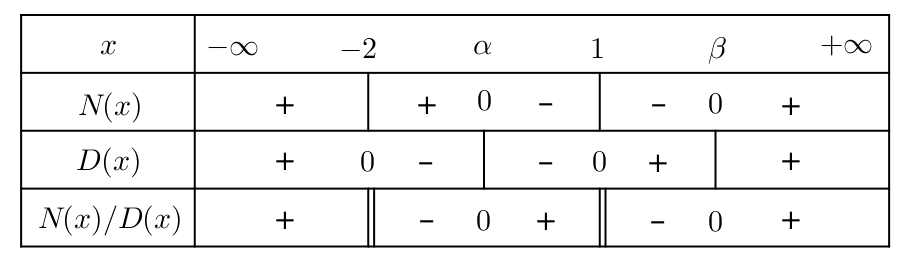
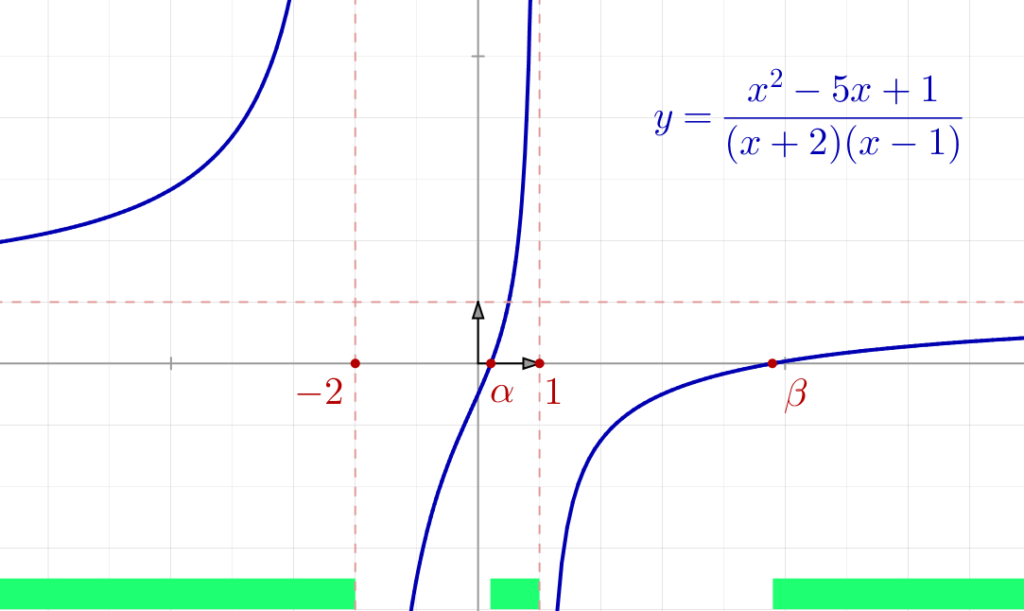
En conclusion, l’ensemble de solutions est :
![]()
A titre indicatif, voici l’allure du graphe de
On voit, indiqué en vert clair au bas du graphe, une représentation de ![]() :
:

On note ![]()
![]() et
et ![]() les ensembles de solutions.
les ensembles de solutions.
- Pour tout
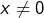 :
:
Les racines du trinôme![Rendered by QuickLaTeX.com \[x+2>\frac{1}{x}\Leftrightarrow\frac{x^{2}+2x-1}{x}>0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-13d9f7f1478c4500f4f72899931d789a_l3.png)
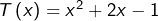 sont :
sont :
Donc![Rendered by QuickLaTeX.com \[\alpha=-1-\sqrt{2}\qquad\text{et}\qquad\beta=-1+\sqrt{2}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a2d5ab292b5521d1b243006331fb1612_l3.png)
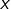 est solution si, et seulement si
est solution si, et seulement si 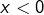 et
et 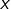 intérieur à
intérieur à ![Rendered by QuickLaTeX.com \left[\alpha,\beta\right]](https://math-os.com/wp-content/ql-cache/quicklatex.com-5ad5ad60fe4c9987c56b811180858bf1_l3.png) ou bien si
ou bien si 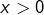 et
et 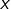 extérieur à
extérieur à ![Rendered by QuickLaTeX.com \left[\alpha,\beta\right];](https://math-os.com/wp-content/ql-cache/quicklatex.com-f0caeda9a9e1a2ca348937ddb67c8d1d_l3.png) autrement dit :
autrement dit :
soit finalement :![Rendered by QuickLaTeX.com \[S_1=\left(\left]\alpha,\beta\right[\cap\left]-\infty,0\right[\right)\cup\left(\left(\left]-\infty,\alpha\right[\cup\left]\beta,+\infty\right[\right)\cap\left]0,+\infty\right[\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-9114e0353d890d5498405df2462a5936_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{S_1=\left]-1-\sqrt{2},0\right[\cup\left]-1+\sqrt{2},+\infty\right[}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-1757caead6ce0a3b0fca88f4720a7382_l3.png)
- Pour tout
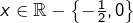 :
:
Posons :![Rendered by QuickLaTeX.com \[\frac{1}{x}+\frac{1}{2x+1}>\frac{5}{2}\Leftrightarrow\frac{10x^{2}-x-2}{2x\left(2x+1\right)}<0 \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a4ee6c5bf39e5dbaa3e1621a9a83187a_l3.png)
Les racines de![Rendered by QuickLaTeX.com \[ N\left(x\right)=10x^{2}-x-2\qquad\text{et}\qquad D\left(x\right)=2x\left(2x+1\right) \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a4fc773ef48071e4ba250eca3a273ad4_l3.png)
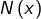 sont :
sont :
En construisant au besoin un tableau de signe, on voit alors que :![Rendered by QuickLaTeX.com \[ \gamma=-\frac{2}{5}\qquad\text{et}\qquad\delta=\frac{1}{2} \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-167e199ad8acc12e0fbdcd44e0037580_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{S_2=\left]-\frac{1}{2},-\frac{2}{5}\right[\cup\left]0,\frac{1}{2}\right[} \]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bb310555a8a156781a33cdb042c4bdad_l3.png)
- Pour tout
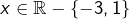 :
:
d’où, après un éventuel tableau de signe :![Rendered by QuickLaTeX.com \[\frac{x\left(x-2\right)}{\left(x-1\right)\left(x+3\right)}>1\Leftrightarrow\frac{4x-3}{\left(x-1\right)\left(x+3\right)}<0\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-7d679cd030e068dcebcad7e1802e1c10_l3.png)
![Rendered by QuickLaTeX.com \[\boxed{S_3=\left]-\infty,-3\right[\cup\left]\frac{3}{4},1\right[}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-ec6785cf7302e595e751316a4930b221_l3.png)

Principe du calcul
Considérons un trinôme ![]() avec
avec ![]() et
et ![]()
Notons ![]() ses racines, avec
ses racines, avec ![]()
On sait que, pour tout ![]() :
:
![]()
et, par conséquent, que :
![Rendered by QuickLaTeX.com \[T\left(x\right)\left\{ \begin{array}{cc}>0 & \text{si }x<\alpha\text{ ou }x>\beta\\ \\ <0 & \text{si }\alpha<x<\beta\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-6560c715a7c443215f6553db1e6ecdf2_l3.png)
Ceci permet de décider, pour un réel
Dans le cas particulier proposé, on calcule :
![]()
![]()
![]()

Il faut déjà que ![]() pour qu’il s’agisse d’un « vrai » trinôme (pour
pour qu’il s’agisse d’un « vrai » trinôme (pour ![]() l’équation est du premier degré et ne possède évidemment qu’une seule solution). En notant
l’équation est du premier degré et ne possède évidemment qu’une seule solution). En notant ![]() le discriminant, il faut en outre que :
le discriminant, il faut en outre que :
![]()
![]()
ou encore :
![]()
![]()
![Rendered by QuickLaTeX.com \[ \boxed{m\in\left]-1-\frac{2\sqrt{3}}{3},0\right[\cup\left]0,-1+\frac{2\sqrt{3}}{3}\right[}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-2b94f345f0935dc7cc025f0a51877d13_l3.png)

Notons ![]() le discriminant du trinôme :
le discriminant du trinôme :
![]()
On cherche les réels ![]() pour lesquels :
pour lesquels :
![]()
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{ccc}\left(2m+1\right)^{2}-4\left(m^{2}+1\right) & > & 0\\\\m^{2}+1-2\left(2m+1\right) & < & 0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b6302148d9f2319c2222adef54b0a6bb_l3.png)
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{ccc} 4m-3 & > & 0\\\\m^{2}-4m-1 & < & 0\end{array}\right.\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-b47399c8c330dc47da00ce0125a91590_l3.png)
Les racines du trinôme ![]() sont :
sont :
![]()
![]()
![Rendered by QuickLaTeX.com \[ \boxed{m\in\left]\frac{3}{4},\thinspace2+\sqrt{5}\right[}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-769cb8e31d3aca31c27e8fa326aba3ec_l3.png)

On sait (somme et produit des racines d’un trinôme) que :
![]()
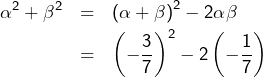
![Rendered by QuickLaTeX.com \[ \boxed{\alpha^{2}+\beta^{2}=\frac{23}{49}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-772c16976da3a9d7ef4b2bc04df94281_l3.png)
De même :
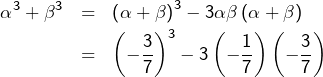
![Rendered by QuickLaTeX.com \[ \boxed{\alpha^{3}+\beta^{3}=-\frac{90}{343}}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-838f5e903ffcaac0a1714ed33374e905_l3.png)
Enfin :
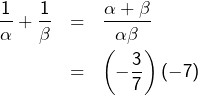
![Rendered by QuickLaTeX.com \[ \boxed{\frac{1}{\alpha}+\frac{1}{\beta}=3}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-fad1639e6bc9e712a07078acbb46f8d1_l3.png)
Cet question est présentée de manière visuelle dans cette vidéo que je vous invite à consulter.
Le sommet ![]() de la parabole est le point d’abscisse :
de la parabole est le point d’abscisse :
![Rendered by QuickLaTeX.com \[ \boxed{X=-\frac{b}{2a}}\qquad\left(\clubsuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-55ef30ef9feccab888e4c840ec96b750_l3.png)
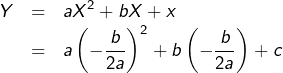
![Rendered by QuickLaTeX.com \[ \boxed{Y=c-\frac{b^{2}}{4a}}\qquad\left(\spadesuit\right)\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a5732d6de150dc8642e9e4163f7f7a39_l3.png)
Il faut maintenant éliminer le paramètre ![]() entre ces deux relations, afin d’obtenir une équation cartésienne du lieu de
entre ces deux relations, afin d’obtenir une équation cartésienne du lieu de ![]() lorsque
lorsque ![]() varie. En remplaçant
varie. En remplaçant ![]() par
par ![]() dans
dans ![]() on obtient :
on obtient :
![]()
Lorsque ![]() parcourt
parcourt ![]() on voit avec la relation
on voit avec la relation ![]() qu’il en va de même pour
qu’il en va de même pour ![]() Le lieu cherché est donc la parabole d’équation
Le lieu cherché est donc la parabole d’équation ![]() toute entière.
toute entière.

- On suppose que
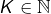 et que
et que 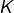 n’est pas un carré parfait. En utilisant le test des racines rationnelles, on voit que si l’équation
n’est pas un carré parfait. En utilisant le test des racines rationnelles, on voit que si l’équation 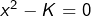 possédait une solution rationnelle, celle-ci serait de la forme
possédait une solution rationnelle, celle-ci serait de la forme
avec![Rendered by QuickLaTeX.com \[\alpha=\frac{p}{q}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-d0aacb2f85361ecb9b7a000d3e13d6be_l3.png)
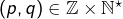 vérifiant les conditions :
vérifiant les conditions :
Mais alors![Rendered by QuickLaTeX.com \[p\mid K\qquad\text{et}\qquad q\mid1\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-a800e274599f0397fb2ba80018a16dae_l3.png)
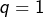 et donc
et donc 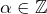 … ce qui est exclu !
… ce qui est exclu ! 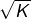 est donc irrationnel.
est donc irrationnel. - On a montré au point précédent qu’étant donné un entier naturel
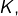 si
si 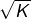 est rationnel, alors
est rationnel, alors 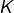 est un carré parfait.
est un carré parfait. - Le carré d’un nombre impair est congru à 1 modulo 8. Par conséquent :
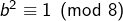 et
et 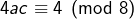 et donc
et donc 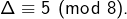
- Les solutions de l’équation
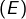 sont :
sont :
On sait que :![Rendered by QuickLaTeX.com \[\alpha=\frac{-b+\sqrt{\Delta}}{2a}\qquad\beta=\frac{-b-\sqrt{\Delta}}{2a}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-bd106ffee7a60ec95483e218d76bf00c_l3.png)
Donc si l’un des deux nombres![Rendered by QuickLaTeX.com \[\alpha+\beta=-\frac{b}{a}\in\mathbb{Q}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-029ca3d3730398a580ce7dd2a0529225_l3.png)
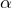 ou
ou 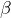 est rationnel, alors l’autre aussi et donc
est rationnel, alors l’autre aussi et donc 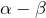 aussi. Or :
aussi. Or :
et donc![Rendered by QuickLaTeX.com \[\alpha-\beta=\frac{\sqrt{\Delta}}{a}\]](https://math-os.com/wp-content/ql-cache/quicklatex.com-e05d36022095c8a2219afcd8ba41603c_l3.png)
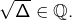 D’après le 2), ceci entraîne que
D’après le 2), ceci entraîne que 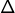 est un carré parfait, donc est congru à
est un carré parfait, donc est congru à 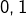 ou
ou 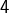 modulo
modulo 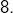 Ceci est en contradiction avec le calcul du 3).
Ceci est en contradiction avec le calcul du 3).
Finalement, les solutions de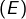 sont toutes deux irrationnelles.
sont toutes deux irrationnelles.
Si un point n’est pas clair ou vous paraît insuffisamment détaillé, n’hésitez pas à poster un commentaire ou à me joindre via le formulaire de contact.
